Dernier essai le
- Score :
/20
Énoncé
Énoncé
Sujet
L'épreuve est notée sur 20. Une note globale égale ou inférieure à 5 est éliminatoire. Durée de l'épreuve : 3 h ; coefficient 1Le sujet est composé de 6 exercices indépendants permettant de vérifier les connaissances du candidat.
Corrigé
Corrigé
Exercice 1
1.
Si l'on choisit l'organisme A, alors il faudra payer 1 500 + 100 × 24 soit 3 900 €.
Si l'on choisit l'organisme B, alors il faudra payer 2 000 + 85 × 24 soit 4 040 €.
On a 3 900 < 4 040 donc l'organisme proposant le devis le plus avantageux est l'organisme A.
Si l'on choisit l'organisme B, alors il faudra payer 2 000 + 85 × 24 soit 4 040 €.
On a 3 900 < 4 040 donc l'organisme proposant le devis le plus avantageux est l'organisme A.
2.
a.
a.
Pour tout entier x compris entre 1 et 110 on a :
f(x) = 1 500 + 100 × x
f(x) = 100x + 1 500
et
g(x) = 2 000 + 85 × x
g(x) = 85x + 2 000
f(x) = 1 500 + 100 × x
f(x) = 100x + 1 500
et
g(x) = 2 000 + 85 × x
g(x) = 85x + 2 000
b.
Résolvons l'équation f(x) = 4 300 (avec x entier compris entre 1 et 110).
f(x) = 4 300 est une équation linéaire du 1er degré à une inconnue (c'est-à-dire du type ax + b = cx + d avec a = 100, b = 1 500, c = 0 et d = 4 300).
On doit donc isoler l'inconnue x (dans le membre de gauche par exemple).
Soit 100x + 1 500 = 4 300
On soustrait par 1 500 les deux membres de l'égalité :
Soit 100x + 1 500 − 1 500 = 4 300 − 1 500
D'où 100x = 2 800
On divise par 100 les deux membres de l'égalité :
Ainsi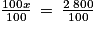
Donc x = 28
Ainsi le coût en euros du voyage scolaire par l'organisme A sera de 4 300 euros uniquement (car une seule solution) pour un groupe de 28 élèves.
f(x) = 4 300 est une équation linéaire du 1er degré à une inconnue (c'est-à-dire du type ax + b = cx + d avec a = 100, b = 1 500, c = 0 et d = 4 300).
On doit donc isoler l'inconnue x (dans le membre de gauche par exemple).
Soit 100x + 1 500 = 4 300
On soustrait par 1 500 les deux membres de l'égalité :
Soit 100x + 1 500 − 1 500 = 4 300 − 1 500
D'où 100x = 2 800
On divise par 100 les deux membres de l'égalité :
Ainsi
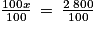
Donc x = 28
Ainsi le coût en euros du voyage scolaire par l'organisme A sera de 4 300 euros uniquement (car une seule solution) pour un groupe de 28 élèves.
c.
On cherche le plus petit entier x (compris entre 1 et 110) tel que g(x) < f(x) (coût du voyage organisé par B strictement inférieur au coût du voyage organisé par A).
g(x) < f(x)
85x + 2 000 < 100x + 1 500
On va encore isoler l'inconnue x dans le membre de gauche car on a une inéquation linéaire du premier degré à une inconnue.
On va soustraire les deux membres par 100x ; le symbole ne change pas de sens :
85x + 2 000 − 100x < 100x + 1 500 − 100x
Soit :
−15x + 2 000 < 1 500
On va soustraire par 2 000 les deux membres ; le symbole ne change pas de sens :
−15x + 2 000 − 2 000 < 1 500 − 2 000
Soit :
−15x < −500
Enfin, on va diviser les deux membres par −15 le symbole change de sens car −15 < 0 :
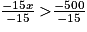
Soit :
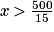
Or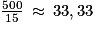 . Donc le plus petit entier recherché est l'entier 34.
. Donc le plus petit entier recherché est l'entier 34.
À partir de 34 élèves, il faut donc choisir l'organisme B.
g(x) < f(x)
85x + 2 000 < 100x + 1 500
On va encore isoler l'inconnue x dans le membre de gauche car on a une inéquation linéaire du premier degré à une inconnue.
On va soustraire les deux membres par 100x ; le symbole ne change pas de sens :
85x + 2 000 − 100x < 100x + 1 500 − 100x
Soit :
−15x + 2 000 < 1 500
On va soustraire par 2 000 les deux membres ; le symbole ne change pas de sens :
−15x + 2 000 − 2 000 < 1 500 − 2 000
Soit :
−15x < −500
Enfin, on va diviser les deux membres par −15 le symbole change de sens car −15 < 0 :
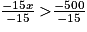
Soit :
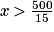
Or
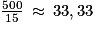 . Donc le plus petit entier recherché est l'entier 34.
. Donc le plus petit entier recherché est l'entier 34.À partir de 34 élèves, il faut donc choisir l'organisme B.
3.
a.
Soit C le coût total.
La mairie va payer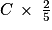 . C'est-à-dire
. C'est-à-dire 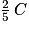 .
.
Le reste du coût total sera donc égal à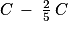 .
.
Or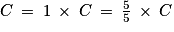 .
.
Ainsi, le reste du coût total sera égal à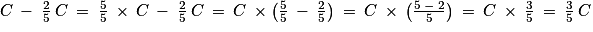 .
.
La coopérative scolaire prendra à sa charge 50 % de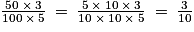 (en divisant le numérateur et le dénominateur par 10 et par 5).
(en divisant le numérateur et le dénominateur par 10 et par 5).
Ainsi, la charge des familles sera de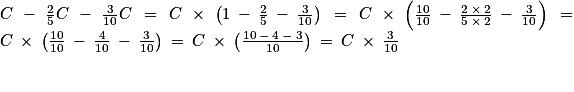 .
.
Ainsi, les familles devront payer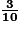 du coût total du voyage.
du coût total du voyage.
Soit C le coût total.
La mairie va payer
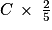 . C'est-à-dire
. C'est-à-dire 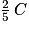 .
.Le reste du coût total sera donc égal à
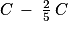 .
.Or
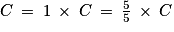 .
.Ainsi, le reste du coût total sera égal à
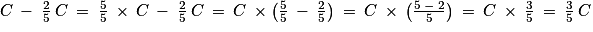 .
.La coopérative scolaire prendra à sa charge 50 % de
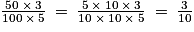 (en divisant le numérateur et le dénominateur par 10 et par 5).
(en divisant le numérateur et le dénominateur par 10 et par 5).Ainsi, la charge des familles sera de
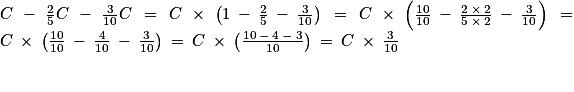 .
.Ainsi, les familles devront payer
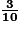 du coût total du voyage.
du coût total du voyage.b.
g(44) = 85 × 44 + 2 000 = 5 740. Ainsi, le coût total est de 5 740 €.
La coopérative finance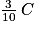 €, soit ici
€, soit ici 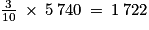 €.
€.
La prise en charge par élève est égale à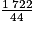 , soit environ 39 €.
, soit environ 39 €.
La coopérative finance
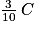 €, soit ici
€, soit ici 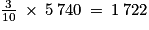 €.
€.La prise en charge par élève est égale à
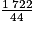 , soit environ 39 €.
, soit environ 39 €.Exercice 2
1.
Il n'y a qu'une seule issue pour pouvoir obtenir une somme égale à 3 : les jetons doivent tous montrer la face indiquant le nombre 1.
On estime que l'expérience est une situation d'équiprobabilité et que les deux issues (obtenir la face 1 et obtenir la face 0) sont équiprobables, la pièce étant équilibrée. Ainsi, la probabilité d'obtenir la face 1 en lançant une pièce est égale à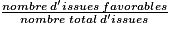 soit
soit 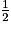 .
.
Enfin, on admet que les trois lancers sont indépendants les uns des autres (le résultat du lancer d'une pièce n'a pas d'influence sur le résultat d'une autre pièce). Ainsi, la probabilité d'obtenir trois fois la face 1 est égale au produit des probabilités d'obtenir la face 1 pour chaque lancer, soit :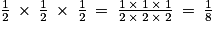 .
.
On estime que l'expérience est une situation d'équiprobabilité et que les deux issues (obtenir la face 1 et obtenir la face 0) sont équiprobables, la pièce étant équilibrée. Ainsi, la probabilité d'obtenir la face 1 en lançant une pièce est égale à
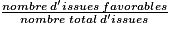 soit
soit 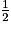 .
.Enfin, on admet que les trois lancers sont indépendants les uns des autres (le résultat du lancer d'une pièce n'a pas d'influence sur le résultat d'une autre pièce). Ainsi, la probabilité d'obtenir trois fois la face 1 est égale au produit des probabilités d'obtenir la face 1 pour chaque lancer, soit :
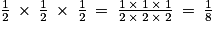 .
.2.
Jeanne a raison.
Voici les huit résultats possibles : 000 ; 001 ; 010 ; 011 ; 100 ; 101 ; 110 ; 111.
On observe bien à chaque fois au moins deux fois le même résultat (au moins deux 0 ou au moins deux 1).
On pouvait l'anticiper, car il n'y a que deux résultats possibles et on lance trois pièces. On a donc 2 < 3.
Voici les huit résultats possibles : 000 ; 001 ; 010 ; 011 ; 100 ; 101 ; 110 ; 111.
On observe bien à chaque fois au moins deux fois le même résultat (au moins deux 0 ou au moins deux 1).
On pouvait l'anticiper, car il n'y a que deux résultats possibles et on lance trois pièces. On a donc 2 < 3.
3.
Olivier n'a pas raison.
Parmi les huit résultats possibles, seuls deux résultats (000 et 111) donnent trois résultats identiques.
Ainsi, la probabilité que les trois jetons indiquent la même face est égale à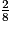 , c'est-à-dire à
, c'est-à-dire à 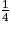 .
.
On a donc une chance sur quatre d'obtenir trois faces identiques.
Parmi les huit résultats possibles, seuls deux résultats (000 et 111) donnent trois résultats identiques.
Ainsi, la probabilité que les trois jetons indiquent la même face est égale à
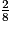 , c'est-à-dire à
, c'est-à-dire à 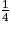 .
.On a donc une chance sur quatre d'obtenir trois faces identiques.
Exercice 3
Partie A
1.
Le volume V d'un parallélépipède rectangle (pavé droit) est égal au produit l × L × h avec l la longueur, L la largeur et h la hauteur.
On vérifie que les grandeurs sont bien toutes exprimées dans la même unité.
V = 30 × 15 × 3 = 1 350
Ainsi, le volume de la fosse est égal à 1 350 m3.
On vérifie que les grandeurs sont bien toutes exprimées dans la même unité.
V = 30 × 15 × 3 = 1 350
Ainsi, le volume de la fosse est égal à 1 350 m3.
2.
Augmenter un nombre positif a de t% revient à multiplier ce nombre a par le coefficient multiplicateur 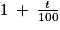 .
.
Notons V2 le volume de terre à évacuer :
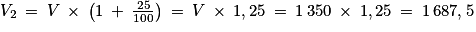
Ainsi, il faudra évacuer 1 687,5 m3 de terre.
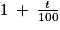 .
.Notons V2 le volume de terre à évacuer :
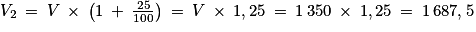
Ainsi, il faudra évacuer 1 687,5 m3 de terre.
3.
Notons n le nombre de bennes nécessaires. n est donc un nombre entier. Il faut que la capacité de stockage soit supérieure ou égale au volume de terre à transporter.
Une benne pouvant contenir 30 m3 de terre, alors par proportionnalité, n bennes peuvent contenir 30 × nm3.
On doit donc trouver le plus petit entier n tel que : 30 × n 1 687,5.
1 687,5.
30 × n 1 687,5
1 687,5
On va diviser les deux membres de cette inéquation par 30 afin d'isoler n. Comme 30 > 0, alors le symbole ne change pas de sens :
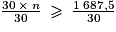
n 56,25
56,25
Ainsi, il faudra au minimum 57 bennes pour évacuer toute la terre.
Une benne pouvant contenir 30 m3 de terre, alors par proportionnalité, n bennes peuvent contenir 30 × nm3.
On doit donc trouver le plus petit entier n tel que : 30 × n
 1 687,5.
1 687,5.30 × n
 1 687,5
1 687,5On va diviser les deux membres de cette inéquation par 30 afin d'isoler n. Comme 30 > 0, alors le symbole ne change pas de sens :
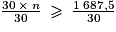
n
 56,25
56,25Ainsi, il faudra au minimum 57 bennes pour évacuer toute la terre.
Partie B
1.
Considérons une grandeur (ici le volume d'eau) mesurée à deux reprises : au départ et à l'arrivée.
On note ces valeurs Vd et Va.
Alors le pourcentage d'évolution entre Vd et Va est le nombre égal à :
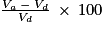
On calcule ainsi :
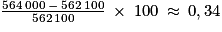
Ainsi le volume d'eau a augmenté d'environ 0,34 %.
On note ces valeurs Vd et Va.
Alors le pourcentage d'évolution entre Vd et Va est le nombre égal à :
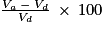
On calcule ainsi :
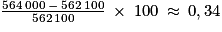
Ainsi le volume d'eau a augmenté d'environ 0,34 %.
2.
Étant donné que 1 litre est égal à 1 dm3, alors :
564 000 L = 564 000 dm3
Or 1 000 dm3 = 1 m3.
Ainsi :
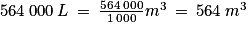
On peut aussi le justifier à l'aide de ce tableau de conversion :
On cherche la hauteur h (nombre réel positif) telle que :
l × L × h = 564 000
Soit :
25 × 12,5 × h = 564
312,5h = 564
On divise les deux membres de l'équation par 312,5 :
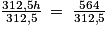
h = 1,8048
Ainsi, la hauteur de l'eau (depuis le fond du bassin) est égale à 1,8048 m soit environ 1,80 m.
564 000 L = 564 000 dm3
Or 1 000 dm3 = 1 m3.
Ainsi :
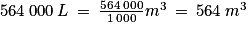
On peut aussi le justifier à l'aide de ce tableau de conversion :
| m3 | dm3 (= litres) | ||||
| 5 | 6 | 4 | 0 | 0 | 0 |
On cherche la hauteur h (nombre réel positif) telle que :
l × L × h = 564 000
Soit :
25 × 12,5 × h = 564
312,5h = 564
On divise les deux membres de l'équation par 312,5 :
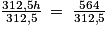
h = 1,8048
Ainsi, la hauteur de l'eau (depuis le fond du bassin) est égale à 1,8048 m soit environ 1,80 m.
Partie C
1.
On a la formule suivante :
Vitesse moyenne =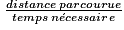
La distance parcourue est égale à : 16 × 25 m = 400 m car une longueur mesure 25 mètres.
Ainsi, la vitesse moyenne en mètres par minute est égale à :
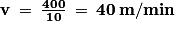
La distance parcourue en kilomètres est égale à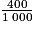 soit 0,4 km.
soit 0,4 km.
On peut également le justifier grâce à ce tableau de conversion :
Le temps nécessaire en heures peut se déterminer grâce à ce tableau de proportionnalité :
On a donc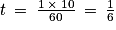 .
.
Ainsi la vitesse moyenne en km/h est égale à :
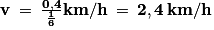
Vitesse moyenne =
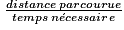
La distance parcourue est égale à : 16 × 25 m = 400 m car une longueur mesure 25 mètres.
Ainsi, la vitesse moyenne en mètres par minute est égale à :
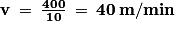
La distance parcourue en kilomètres est égale à
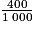 soit 0,4 km.
soit 0,4 km.On peut également le justifier grâce à ce tableau de conversion :
| km | hm | dam | m | dm | cm | mm |
| | 4 | 0 | 0 | | | |
Le temps nécessaire en heures peut se déterminer grâce à ce tableau de proportionnalité :
| Heures | 1 | t |
| Minutes | 60 | 10 |
On a donc
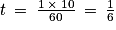 .
.Ainsi la vitesse moyenne en km/h est égale à :
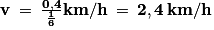
2.
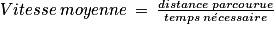
Donc :
distance parcourue = Vitesse moyenne × temps nécessaire
Il faut dans un premier temps convertir la durée en secondes.
| Minutes | 1 | 10 |
| Secondes | 60 | x |
On a donc
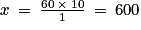 . Donc l'élève a nagé pendant 600 s.
. Donc l'élève a nagé pendant 600 s.La vitesse étant donnée en m/s, alors on peut calculer la distance parcourue en mètres :
d = v × t = 0,6 × 600 = 360
Ainsi, l'élève a parcouru 360 mètres.
Or, une longueur mesure 25 mètres. On cherche donc le nombre de longueurs complètes effectuées ; on cherche donc le quotient dans la division euclidienne de 360 par 25.
Or
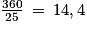 . Donc l'élève a parcouru 14 longueurs complètes.
. Donc l'élève a parcouru 14 longueurs complètes.Attention : si l'on détermine le plus petit entier n tel que 25 × n
 360, alors on trouvera 15, ce qui ne répond pas à la question posée.
360, alors on trouvera 15, ce qui ne répond pas à la question posée.3.
a.
a.
B3 = B2*25
b.
Parmi les neuf élèves, on en compte six qui ont nagé au moins 12 longueurs.
La proportion est donc égale à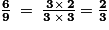 .
.
La proportion est donc égale à
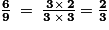 .
.c.
On doit dans un premier temps ranger les valeurs dans l'ordre croissant.
10 – 11 – 11 – 12 – 13 – 14 – 14 – 15 – 16
On a un effectif total (nombre total de valeurs) égal à 9.
Or, 9 est un entier impair. La médiane est donc la valeur centrale de la liste des valeurs.
Ainsi, la médiane est égale à 13.
Cela signifie qu'au moins 50 % des élèves ont nagé au moins 13 longueurs ; ou encore qu'au moins la moitié des élèves ont nagé au plus 13 longueurs.
10 – 11 – 11 – 12 – 13 – 14 – 14 – 15 – 16
On a un effectif total (nombre total de valeurs) égal à 9.
Or, 9 est un entier impair. La médiane est donc la valeur centrale de la liste des valeurs.
Ainsi, la médiane est égale à 13.
Cela signifie qu'au moins 50 % des élèves ont nagé au moins 13 longueurs ; ou encore qu'au moins la moitié des élèves ont nagé au plus 13 longueurs.
d.
La moyenne arithmétique est égale ici au rapport entre la somme des valeurs et l'effectif total :
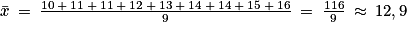
Ainsi, chaque élève a effectué en moyenne 12,9 longueurs.
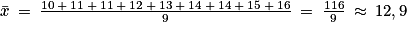
Ainsi, chaque élève a effectué en moyenne 12,9 longueurs.
e.
On cherche un nombre positif n (à priori entier) tel que :
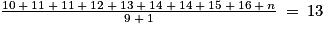
Soit :
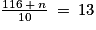
On multiplie les deux membres de l'équation par 10 :
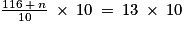
116 + n = 130
On soustrait les deux membres par 116 pour isoler n :
116 + n − 116 = 130 − 116
Ainsi :
n = 14
Il faut donc que l'élève absent arrive à effectuer exactement 14 longueurs afin que le nouveau nombre moyen de longueurs du groupe soit égal à 13.
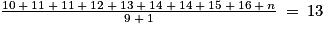
Soit :
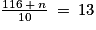
On multiplie les deux membres de l'équation par 10 :
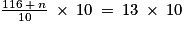
116 + n = 130
On soustrait les deux membres par 116 pour isoler n :
116 + n − 116 = 130 − 116
Ainsi :
n = 14
Il faut donc que l'élève absent arrive à effectuer exactement 14 longueurs afin que le nouveau nombre moyen de longueurs du groupe soit égal à 13.
Exercice 4
1.
Il suffit de choisir a = 45. On a alors 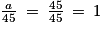 .
.
On peut aussi choisir tout autre multiple de 45.
En effet, si a est un multiple de 45, alors il existe un unique nombre entier positif k tel que a = 45 × k et dans ce cas :
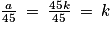
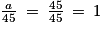 .
.On peut aussi choisir tout autre multiple de 45.
En effet, si a est un multiple de 45, alors il existe un unique nombre entier positif k tel que a = 45 × k et dans ce cas :
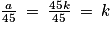
2.
On cherche en fait les diviseurs entiers du nombre 45.
En effet :
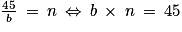
Les diviseurs de 45 sont : 1, 3, 5, 9, 15 et 45.
On sait que 45 est divisible par 3 car 4 + 5 = 9 et 9 est divisible par 3.
On sait que 45 est divisible par 5 car 45 se termine par un 5.
Ainsi, toutes les valeurs de b telles que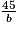 est entier naturel sont les entiers : 1, 3, 5, 9, 15 et 45.
est entier naturel sont les entiers : 1, 3, 5, 9, 15 et 45.
En effet :
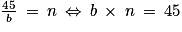
Les diviseurs de 45 sont : 1, 3, 5, 9, 15 et 45.
On sait que 45 est divisible par 3 car 4 + 5 = 9 et 9 est divisible par 3.
On sait que 45 est divisible par 5 car 45 se termine par un 5.
Ainsi, toutes les valeurs de b telles que
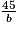 est entier naturel sont les entiers : 1, 3, 5, 9, 15 et 45.
est entier naturel sont les entiers : 1, 3, 5, 9, 15 et 45.3.
Si l'on choisit par exemple c = 9, alors on a 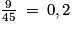 .
.
On peut aussi se fixer le résultat et en déduire ainsi la valeur de c. Par exemple, si l'on souhaite obtenir le nombre décimal non entier 1,2, alors on résout l'équation :
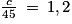
On multiplie les deux membres de l'équation par 45.
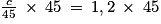
c = 54
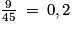 .
.On peut aussi se fixer le résultat et en déduire ainsi la valeur de c. Par exemple, si l'on souhaite obtenir le nombre décimal non entier 1,2, alors on résout l'équation :
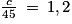
On multiplie les deux membres de l'équation par 45.
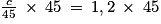
c = 54
4.
Il suffit de choisir d = 2, car 45 n'est pas divisible par 2. On a alors 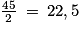 .
.
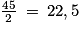 .
.5.
Un nombre rationnel est un nombre pouvant s'écrire comme un rapport (un ratio) entre deux nombres entiers.
Certains nombres rationnels ne sont pas décimaux comme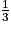 par exemple.
par exemple.
En effet, il n'existe pas d'écriture décimale finie pour écrire le nombre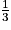 .
.
On peut donc chercher la valeur de e telle que :
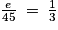
On multiplie les deux membres de l'équation par 45.
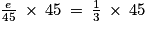
Ainsi :
e = 15
Certains nombres rationnels ne sont pas décimaux comme
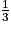 par exemple.
par exemple.En effet, il n'existe pas d'écriture décimale finie pour écrire le nombre
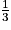 .
.On peut donc chercher la valeur de e telle que :
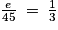
On multiplie les deux membres de l'équation par 45.
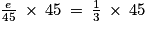
Ainsi :
e = 15
Exercice 5
1.
C'est la figure C qui semble être la plus « grande » et qui a donc la plus grande aire.
2.
C'est la figure H qui semble être la plus « petite » et qui a donc la plus petite aire.
3.
Les figures C, H, I et J ont le même périmètre égal à 3 fois la longueur d'un arc.
En effet, chacune possède trois côtés qui sont des arcs.
Les figures D, F, K et G ont également le même périmètre égal à la somme de longueur d'un côté du triangle initial (non déformé) et de deux fois la longueur d'un arc.
En effet, chacune possède deux côtés qui sont des arcs et un côté qui est un segment.
En effet, chacune possède trois côtés qui sont des arcs.
Les figures D, F, K et G ont également le même périmètre égal à la somme de longueur d'un côté du triangle initial (non déformé) et de deux fois la longueur d'un arc.
En effet, chacune possède deux côtés qui sont des arcs et un côté qui est un segment.
4.
Le couple (A, K) est correct car le segment remplacé par un arc creusé est compensé par le segment suivant qui est remplacé par un arc bombé.
Le couple (B, J) est correct car un segment droit est compensé par un segment bombé et un segment creusé.
De la même manière, le couple (E, I) est correct également.
Le couple (B, J) est correct car un segment droit est compensé par un segment bombé et un segment creusé.
De la même manière, le couple (E, I) est correct également.
Exercice 6
1.
On a SA = SB = AB car SAB est un triangle équilatéral et SB = SC = BC car SBC est équilatéral également.
Ainsi, par transitivité on peut affirmer que :
SA = SC
Donc le triangle ASC est isocèle en S.
De plus, AB = BC = 4 car ABCD est un carré, donc SA = SC = 4.
Le triangle ABC est rectangle en B. Donc d'après le théorème de Pythagore :
AC2 = AB2 + BC2
AC2 = 42 + 42 = 16 + 16 = 32
Donc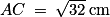 .
.
Déterminons maintenant si le triangle ASC est rectangle en S :
D'une part : AC2 = 32.
D'autre part : SA2 + SC2 = 42 + 42 = 16 + 16 = 32.
On a l'égalité suivante qui est vraie : SA2 + SC2 = AC2.
Ainsi, d'après la réciproque du théorème de Pythagore, le triangle ASC est rectangle en S.
Ainsi, par transitivité on peut affirmer que :
SA = SC
Donc le triangle ASC est isocèle en S.
De plus, AB = BC = 4 car ABCD est un carré, donc SA = SC = 4.
Le triangle ABC est rectangle en B. Donc d'après le théorème de Pythagore :
AC2 = AB2 + BC2
AC2 = 42 + 42 = 16 + 16 = 32
Donc
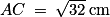 .
.Déterminons maintenant si le triangle ASC est rectangle en S :
D'une part : AC2 = 32.
D'autre part : SA2 + SC2 = 42 + 42 = 16 + 16 = 32.
On a l'égalité suivante qui est vraie : SA2 + SC2 = AC2.
Ainsi, d'après la réciproque du théorème de Pythagore, le triangle ASC est rectangle en S.
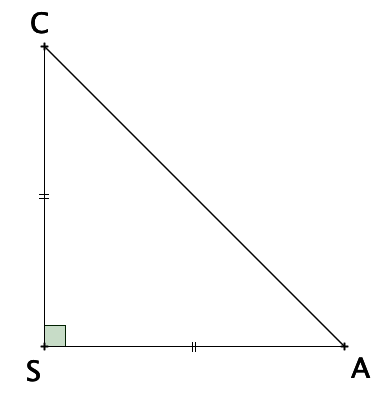 |
On peut en conclure que le triangle ASC est rectangle et isocèle en S.
2.
Figure 3 : on constate directement que deux triangles proposés ne sont pas équilatéraux. Cela ne convient donc pas pour le patron.
Figure 2 : les triangles T3 et T4 vont se superposer et il va donc manquer un triangle.
Figure 1 : c'est bien un patron de la pyramide, car les 4 triangles équilatéraux formeront les 4 côtés de la pyramide en rejoignant chaque arête de la base carrée.
Figure 2 : les triangles T3 et T4 vont se superposer et il va donc manquer un triangle.
Figure 1 : c'est bien un patron de la pyramide, car les 4 triangles équilatéraux formeront les 4 côtés de la pyramide en rejoignant chaque arête de la base carrée.
3.
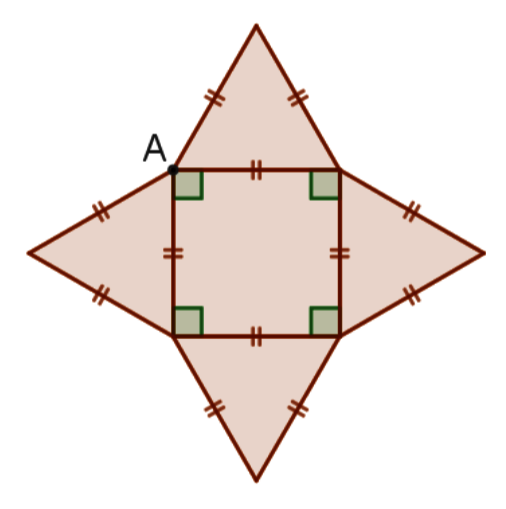 |
Le carré a des côtés de longueurs 4 cm et 1 cm est équivalent à 20 pas du lutin.
On a le tableau de proportionnalité suivant pour trouver le nombre p de pas pour tracer un segment de 4 cm :
Ainsi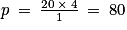 .
.
Donc M = 80.
De plus, les angles dans un carré sont des angles droits, c'est-à-dire de mesure égale à 90° donc N = 90.
Ensuite, les angles dans un triangle équilatéral ont pour mesure 60° donc R = 60.
Les triangles ont des côtés mesurant 4 cm donc P = M = 80.
Enfin il y a quatre triangles, on doit donc avoir T = 4.
Vérifions à l'aide du logiciel Scratch :
On a le tableau de proportionnalité suivant pour trouver le nombre p de pas pour tracer un segment de 4 cm :
| cm | 1 | 4 |
| pas | 20 | p |
Ainsi
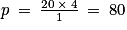 .
.Donc M = 80.
De plus, les angles dans un carré sont des angles droits, c'est-à-dire de mesure égale à 90° donc N = 90.
Ensuite, les angles dans un triangle équilatéral ont pour mesure 60° donc R = 60.
Les triangles ont des côtés mesurant 4 cm donc P = M = 80.
Enfin il y a quatre triangles, on doit donc avoir T = 4.
Vérifions à l'aide du logiciel Scratch :
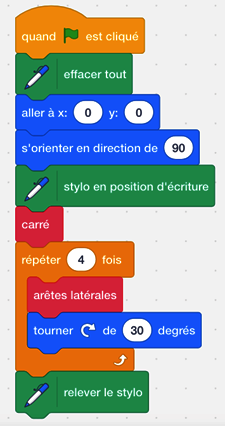 |
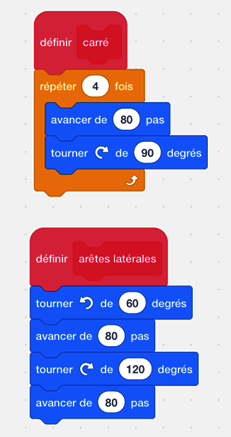 |
On obtient bien le patron demandé :
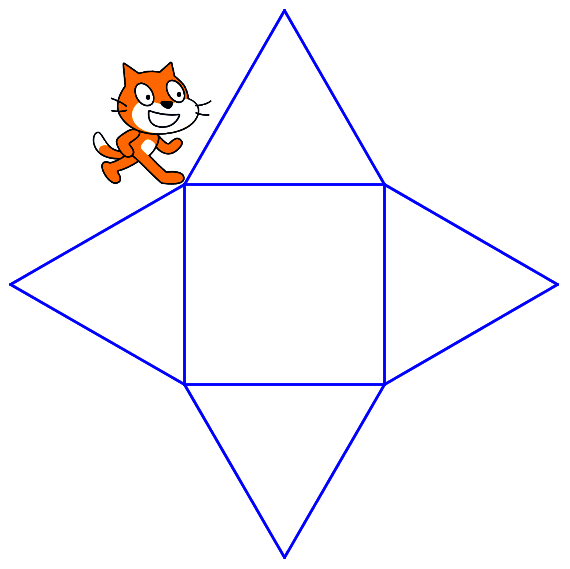 |
Sujet corrigé réalisé par Jean Delautre, professeur de mathématiques au lycée Notre-Dame de la Paix à Lille.
Document suivant
Sujet 2025 de mathématiques, groupement académique 2 (nouveau)
