Dernier essai le
- Score :
/20
Énoncé
Énoncé
Sujet
L'épreuve est notée sur 20. Une note globale égale ou inférieure à 5 est éliminatoire. Durée de l'épreuve : 3 h ; coefficient 1
Le sujet est composé de 5 exercices indépendants permettant de vérifier les connaissances du candidat.
Corrigé
Corrigé
Exercice 1
1.
Affirmation 1 : FAUXOn doit dans un premier temps ranger les nombres dans l'ordre croissant :
4 – 6 – 8 – 9 – 10 – 10 – 12 – 14 – 15 – 16 – 17
La série est constituée de 11 éléments. 11 est un nombre impair.
La médiane est donc égale à la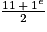 valeur, c'est-à-dire la 6e valeur.
valeur, c'est-à-dire la 6e valeur.
Ainsi la médiane est égale à 10.
Vérification : on a bien au moins 50 % des nombres qui sont supérieurs ou égaux à 10 (10, 10, 12, 14, 15, 16 et 17, soit 7 éléments sur 11, soit environ 63,6 %) et on a bien au moins 50 % des nombres qui sont inférieurs ou égaux à 10 (10, 10, 9, 8, 6, et 4, soit environ 54,5 %).
11 n'est pas la médiane car seuls les éléments 12, 14, 15, 16 et 17 sont supérieurs ou égaux à 11, soit environ 45,4 %.
L'affirmation 1 est donc fausse.
4 – 6 – 8 – 9 – 10 – 10 – 12 – 14 – 15 – 16 – 17
La série est constituée de 11 éléments. 11 est un nombre impair.
La médiane est donc égale à la
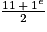 valeur, c'est-à-dire la 6e valeur.
valeur, c'est-à-dire la 6e valeur.Ainsi la médiane est égale à 10.
Vérification : on a bien au moins 50 % des nombres qui sont supérieurs ou égaux à 10 (10, 10, 12, 14, 15, 16 et 17, soit 7 éléments sur 11, soit environ 63,6 %) et on a bien au moins 50 % des nombres qui sont inférieurs ou égaux à 10 (10, 10, 9, 8, 6, et 4, soit environ 54,5 %).
11 n'est pas la médiane car seuls les éléments 12, 14, 15, 16 et 17 sont supérieurs ou égaux à 11, soit environ 45,4 %.
L'affirmation 1 est donc fausse.
Des ressources pour réviser les statistiques sont disponibles sur le site Euler de l'académie de Versailles.
2.
Affirmation 2 : FAUXD'une part :
100 m =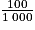 km = 0,1 km
km = 0,1 km
D'autre part :
9,79 s =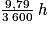
Ainsi, la vitesse moyenne en km/h est égale à :
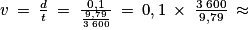 36,77 km/h
36,77 km/h
La vitesse est légèrement inférieure à 37 km/h.
L'affirmation 2 est donc fausse.
100 m =
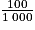 km = 0,1 km
km = 0,1 kmD'autre part :
9,79 s =
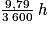
Ainsi, la vitesse moyenne en km/h est égale à :
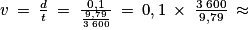 36,77 km/h
36,77 km/hLa vitesse est légèrement inférieure à 37 km/h.
L'affirmation 2 est donc fausse.
3.
Affirmation 3 : FAUXSoit un carré dont les côtés ont pour longueur c avec c un réel strictement positif.
Alors l'aire (de la surface délimitée par) de ce carré est égale à c × c, c'est-à-dire c2.
Simplifions le rapport . On trouve un résultat égal à c. C'est un résultat qui n'est pas égal à une constante indépendante de la variable. On peut donc affirmer qu'il n'y a pas de relation de proportionnalité entre la longueur d'un côté d'un carré et l'aire de ce carré.
. On trouve un résultat égal à c. C'est un résultat qui n'est pas égal à une constante indépendante de la variable. On peut donc affirmer qu'il n'y a pas de relation de proportionnalité entre la longueur d'un côté d'un carré et l'aire de ce carré.
On peut également utiliser un contre-exemple.
Ce tableau n'est pas un tableau de proportionnalité. En effet, pour passer de 10 à 100, on doit multiplier par 10, alors que pour passer de 20 à 400, on doit multiplier par 20. Il n'y a pas un même coefficient multiplicateur pour passer de la première ligne à la seconde ligne, donc ce tableau n'est pas un tableau de proportionnalité.
L'affirmation 3 est donc fausse.
Alors l'aire (de la surface délimitée par) de ce carré est égale à c × c, c'est-à-dire c2.
Simplifions le rapport
 . On trouve un résultat égal à c. C'est un résultat qui n'est pas égal à une constante indépendante de la variable. On peut donc affirmer qu'il n'y a pas de relation de proportionnalité entre la longueur d'un côté d'un carré et l'aire de ce carré.
. On trouve un résultat égal à c. C'est un résultat qui n'est pas égal à une constante indépendante de la variable. On peut donc affirmer qu'il n'y a pas de relation de proportionnalité entre la longueur d'un côté d'un carré et l'aire de ce carré.On peut également utiliser un contre-exemple.
| Longueur d'un côté | 10 | 20 |
|---|---|---|
| Aire du carré | 100 | 400 |
Ce tableau n'est pas un tableau de proportionnalité. En effet, pour passer de 10 à 100, on doit multiplier par 10, alors que pour passer de 20 à 400, on doit multiplier par 20. Il n'y a pas un même coefficient multiplicateur pour passer de la première ligne à la seconde ligne, donc ce tableau n'est pas un tableau de proportionnalité.
L'affirmation 3 est donc fausse.
4.
Affirmation 4 : FAUXOn reconnaît une configuration de Thalès. D'après le théorème de Thalès (car on sait que les droites sont parallèles – on n'utilise la réciproque du théorème que pour prouver que deux droites sont parallèles), on a l'égalité suivante :

Or AC = AB + BC = 3 + 5 = 8. On a donc :
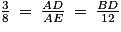
Or on cherche la longueur BD. On va donc utiliser l'égalité :
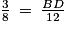
Afin d'isoler BD, on multiplie par 12 les deux membres de l'égalité :
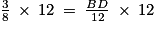
Ainsi :
4,5 = BD
L'affirmation 4 qui dit que BD = 4,4 cm est donc fausse.

Or AC = AB + BC = 3 + 5 = 8. On a donc :
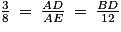
Or on cherche la longueur BD. On va donc utiliser l'égalité :
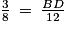
Afin d'isoler BD, on multiplie par 12 les deux membres de l'égalité :
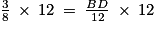
Ainsi :
4,5 = BD
L'affirmation 4 qui dit que BD = 4,4 cm est donc fausse.
Des rappels sur le théorème de Thalès sont disponibles si nécessaire sur le site blogpeda.ac-bordeaux.fr.
Exercice 2
L'indice A indique que le nombre recherché n est un entier et que l'écriture (en base décimale) de n est de la forme MCDU avec 1 M
M  4 et C, D et U des entiers de l'ensemble {0 ;1 ;2 ;3 ;4 ;5 ;6 ;7 ;8 ;9}.
4 et C, D et U des entiers de l'ensemble {0 ;1 ;2 ;3 ;4 ;5 ;6 ;7 ;8 ;9}.(M pour milliers ; C pour centaines ; D pour dizaines et U pour unités).
L'indice F nous donne directement U = 4.
L'indice C nous donne C = 2 × U = 2 × 4 = 8.
L'indice D nous indique que le nombre dont l'écriture est M8 est un multiple de 9.
Les multiples de 9 à deux chiffres sont : 18, 27, 36, 45, 54, 63, 72, 81, 90 et 99.
Ainsi, le seul multiple de 9 possédant un chiffre des unités égal à 8 est 18.
Donc M8 est en fait 18. Donc on a M = 1.
L'indice B nous indique que n est un multiple de 3, donc la somme de ses chiffres est un multiple de 3. Donc M + C + D + U est un multiple de 3.
Or M + C + D + U = 1 + 8 + D + 4 = D + 13.
On rappelle que
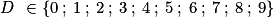
Les entiers possibles sont donc : 2, 5 et 8 pour que D + 13 soit un multiple de 3.
Enfin, l'indice E indique que n n'est pas divisible par 4.
Les trois candidats pour n sont 1 824, 1 854 et 1 884.
Seul 1 854 n'est pas divisible par 4 (car
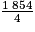 n'est pas un entier).
n'est pas un entier).Ainsi, n = 1 854.
Exercice 3
1.
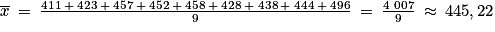
Ainsi, sur la période de 2004 à 2020, la masse moyenne de déchets ménagers collectés par habitant était d'environ 445 kg.
2.
Les ménages ont produit 33,5 Mt ; la production totale était de 310,5 Mt.On calcule donc :
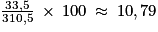
Ainsi, environ 11 % des déchets produits en France sont produits par les ménages.
3.
a. On a le tableau de proportionnalité suivant :
Ainsi, la masse recherchée est égale à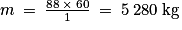 .
.
Or 1 tonne est égale à 1 000 kg donc m = 5,28 tonnes.
On a le tableau de proportionnalité suivant :
Ainsi, par proportionnalité, on a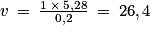 .
.
On peut ainsi prévoir un volume de 26,4 m3 de déchets verts dans ce lotissement de 60 personnes en 2023.
| Nombre d'habitants | 1 | 60 |
|---|---|---|
| Masse de déchets verts (en kg) | 88 | m |
Ainsi, la masse recherchée est égale à
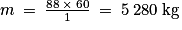 .
.Or 1 tonne est égale à 1 000 kg donc m = 5,28 tonnes.
On a le tableau de proportionnalité suivant :
| Volume des déchets verts (m3) | 1 | v |
|---|---|---|
| Masse correspondante (tonnes) | 0,2 | 5,28 |
Ainsi, par proportionnalité, on a
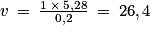 .
.On peut ainsi prévoir un volume de 26,4 m3 de déchets verts dans ce lotissement de 60 personnes en 2023.
b.
On choisit la valeur de m en kg puisque la réponse attendue doit être donnée en kg.On calcule donc :
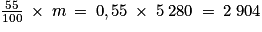
Ainsi, la masse de compost obtenu sera de 2 904 kg.
Remarque : il ne faut pas utiliser de coefficient multiplicateur, car l'énoncé ne donne pas le pourcentage de diminution.
Exercice 4
Des rappels sur les probabilités peuvent être consultés sur les sites de Lumni et du ministère de l'éducation nationale.
Partie A
La modélisation la plus efficace pour un lancer de deux dés est d'utiliser un tableau à double entrée. Un arbre probabiliste serait trop grand, peu lisible et long à réaliser.
On dénombre 60 cases dans le tableau, correspondant aux 10 × 6 couples différents.
L'univers est donc composé de 60 issues.
On est dans le cas d'une situation d'équiprobabilité, car les dés sont équilibrés, chaque couple a donc autant de chances d'apparaître.
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
On dénombre 60 cases dans le tableau, correspondant aux 10 × 6 couples différents.
L'univers est donc composé de 60 issues.
On est dans le cas d'une situation d'équiprobabilité, car les dés sont équilibrés, chaque couple a donc autant de chances d'apparaître.
1.
Une seule case du tableau indique le résultat 35, car seul le couple (5, 7) permet d'obtenir le produit 35.On note A l'événement « le produit obtenu est égal à 35 ».
A est donc composé d'une seule issue.
On a :
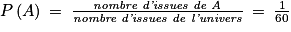
2.
Soit B l'événement « le produit obtenu est 16 ».B est réalisé par les couples (4, 4) et (2, 8). B est donc composé de 2 issues.
Ainsi :
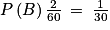
3.
Soit C l'événement « le produit obtenu est un multiple de 3 ».
Beaucoup de couples réalisent C. Pour éviter d'en oublier, on remarque que l'on va devoir sélectionner les lignes et colonnes comportant un multiple de 3, donc les lignes 3 et 6 et les colonnes 3, 6 et 9.
On dénombre ainsi 32 couples réalisant C.
Donc :
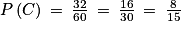
Beaucoup de couples réalisent C. Pour éviter d'en oublier, on remarque que l'on va devoir sélectionner les lignes et colonnes comportant un multiple de 3, donc les lignes 3 et 6 et les colonnes 3, 6 et 9.
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
On dénombre ainsi 32 couples réalisant C.
Donc :
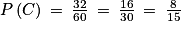
Partie B
Cette décomposition est l'écriture anglo-saxonne des mixed numbers.
1.
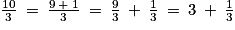
En effet, si l'on écrit 10 autrement, on ne pourra pas obtenir pour le second terme de la somme une fraction inférieure à 1 (c'est-à-dire dont le numérateur est inférieur au dénominateur) ou on ne pourra pas obtenir un nombre entier pour le premier terme de la somme.
2.
L'entier sera égal à 0 si et seulement si la fraction obtenue est déjà elle-même strictement inférieure à 1 (on parle en anglais de fraction propre), c'est-à-dire que le numérateur est strictement inférieur au dénominateur.
Soit D l'événement « le résultat du dé à 10 faces est strictement inférieur au résultat du dé à 6 faces ».
L'événement D est réalisé par 15 couples. Donc D est composé de 15 issues.
Ainsi :
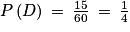
Soit D l'événement « le résultat du dé à 10 faces est strictement inférieur au résultat du dé à 6 faces ».
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
| 3 | 1/3 | 2/3 | 1 | 4/3 | 5/3 | 2 | 7/3 | 8/3 | 3 | 10/3 |
| 4 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 | 2 ,25 | 2,5 |
| 5 | 0,2 | 0,4 | 0,6 | 0,8 | 1 | 1,2 | 1,4 | 1,6 | 1,8 | 2 |
| 6 | 1/6 | 1/3 | 0,5 | 2/3 | 5/6 | 1 | 7/6 | 4/3 | 1,5 | 5/3 |
L'événement D est réalisé par 15 couples. Donc D est composé de 15 issues.
Ainsi :
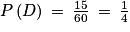
3.
Soit E l'événement « la fraction obtenue est égale à un nombre entier ».
Une fraction positive est égale à un nombre entier si et seulement si son numérateur est un multiple de son dénominateur.
E : « le résultat du dé à 10 faces est un multiple du dé à 6 faces ».
23 couples réalisent l'événement E. E est donc composé de 23 issues.
Ainsi :
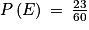
Une fraction positive est égale à un nombre entier si et seulement si son numérateur est un multiple de son dénominateur.
E : « le résultat du dé à 10 faces est un multiple du dé à 6 faces ».
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
| 3 | 1/3 | 2/3 | 1 | 4/3 | 5/3 | 2 | 7/3 | 8/3 | 3 | 10/3 |
| 4 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 | 2 ,25 | 2,5 |
| 5 | 0,2 | 0,4 | 0,6 | 0,8 | 1 | 1,2 | 1,4 | 1,6 | 1,8 | 2 |
| 6 | 1/6 | 1/3 | 0,5 | 2/3 | 5/6 | 1 | 7/6 | 4/3 | 1,5 | 5/3 |
23 couples réalisent l'événement E. E est donc composé de 23 issues.
Ainsi :
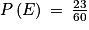
Un document ressource Éduscol sur les probabilités peut être téléchargé ici.
Exercice 5
1.
a.
Le rayon du cuilleron est égal à la moitié de son diamètre, soit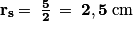 .
.Le volume du cuilleron est égal à la moitié du volume d'une boule de rayon rS = 2,5 cm.
Ainsi :
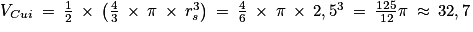
Ainsi, le volume du cuilleron est bien environ égal à 32,7 cm3.
b.
On cherche la hauteur h (h réel positif) du cylindre tel que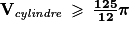 .
.Or :
Vcylindre = Aire du disque de base × hauteur
Vcylindre = π × rC2 × h
Le rayon du cylindre est de rC = 2,5 cm.
On résout donc :
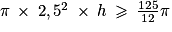
On divise les deux membres par π (le symbole ne change pas de sens car π > 0) :
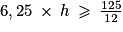
On divise les deux membres par 6,25 (le symbole ne change pas de sens car 6,25 > 0) :
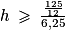
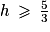
Ainsi, la hauteur minimale du moule de type A doit être d'environ 1,7 cm pour que la cire ne déborde pas.
Des rappels pour réviser les inéquations sont disponibles sur le site Euler de l'académie de Versailles.
c.
Le patron d'un cylindre est composé d'un rectangle et de deux disques.Le rectangle a pour longueur la hauteur h déterminée dans la question précédente.
Le rectangle a pour largeur le périmètre du cercle de la base. Or, ce cercle a pour rayon rC = 2,5 cm, donc la largeur du rectangle est égale à : 2 × π × rC = 2 × π × 2,5 = 5π
 15,7 cm.
15,7 cm.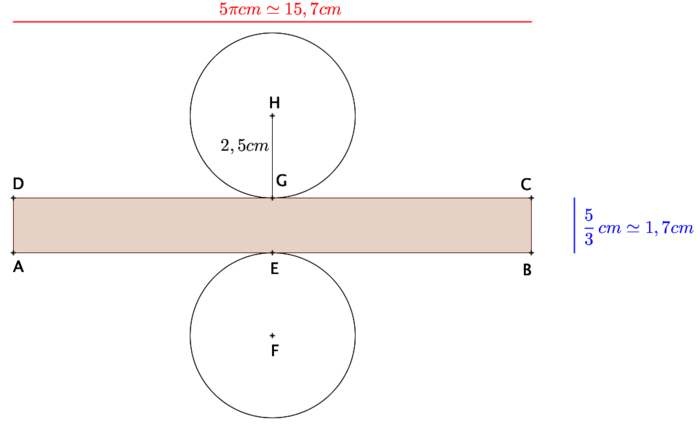 |
2.
a.
Il faut dans un premier temps déterminer le volume du cuilleron en mL.On sait que son volume est égal à
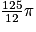 cm3
cm3  32,7 cm3.
32,7 cm3.On possède le tableau de conversion suivant :
| dm3 ( = Litres) | cm3 | mm3 | ||||||
|---|---|---|---|---|---|---|---|---|
| | | 0 | 0 | 3 | 2 | 7 | | |
À retenir : 1 dm3 = 1L.
Pour convertir des cm3 en dm3, on doit donc diviser la valeur par 1 000 (ou la multiplier par 0,001).
Donc :
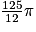 cm3 =
cm3 = 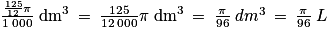
De plus, 1L = 1 000 mL.
| L | dL | cL | mL |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
Ainsi,
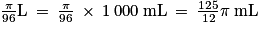 .
.Remarque : on aurait pu prouver directement que 1 cm3 = 1 mL.
Utilisons maintenant un tableau de proportionnalité pour déterminer la masse de cire à chauffer :
| Masse (en g) | 90 | m |
|---|---|---|
| Volume (en mL) | 100 | 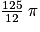 |
Ainsi, par proportionnalité, on a
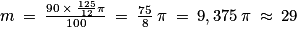 .
.Ainsi, il faudra faire fondre 29 grammes de cire pour remplir le cuilleron.
b.
On dispose de 1 kg de cire, c'est-à-dire 1 000 grammes de cire.Chaque cuilleron va fabriquer une bougie cylindrique de hauteur h et chaque cuilleron contient 9,375 π grammes de cire.
On a donc le tableau de proportionnalité suivant :
| Nombre de bougies | 1 | b |
|---|---|---|
| Masse de cire en g | 9,375 π | 1 000 |
Ainsi, on a :
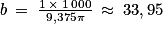
Ainsi, on pourra fabriquer 33 bougies complètes (et une dernière bougie dont la hauteur sera légèrement inférieure à h).
3.
a.
Le carré a des côtés de longueurs 4 cm.On nomme les sommets du carré : A, B, C et D et on nomme les sommets (qui ne sont pas des sommets du carré) des triangles E, F, G et H.
Le triangle ABC est rectangle en B.
D'après le théorème de Pythagore, on a l'égalité suivante :
AC2 = AB2 + BC2
AC2 = 42 + 42
AC2 = 16 + 16
AC2 = 32
AC =
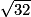
AC
 5,7 cm
5,7 cm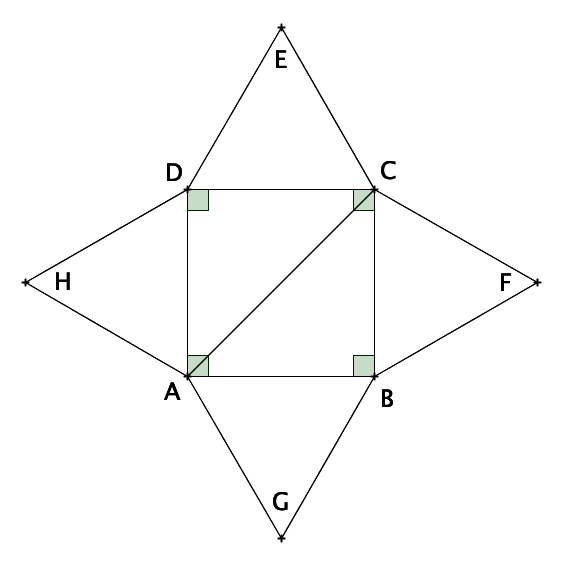 |
C'est bien le théorème que l'on utilise et non sa réciproque. La réciproque du théorème de Pythagore sert à prouver qu'un triangle dont on connaît les longueurs des trois côtés (et à priori quelconque) est rectangle. Or, ici on sait que le triangle est rectangle et on cherche une longueur manquante (ici la longueur de l'hypoténuse).
b.
On note O le centre du carré ABCD. O est donc le milieu du segment [AC].En repliant le patron pour créer la pyramide, les points E, F, G et H sont confondus et on a AE = BE = CE = DE = 4.
La hauteur de la pyramide a pour longueur OE. De plus, le triangle AOE est rectangle en O.
On peut donc utiliser le théorème de Pythagore et on a :
AE2 = AO2 + OE2
Or
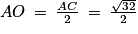 .
.Donc :
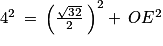
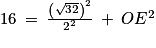
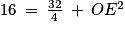
16 = 8 + OE2
On soustrait les deux membres de l'égalité par 8 :
16 − 8 = 8 + OE2 − 8
8 = OE2
OE2 = 8
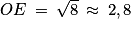
Ainsi, la hauteur de la pyramide est égale à environ 2,8 cm.
c.
Calculons le volume de la pyramide.On a la formule suivante :
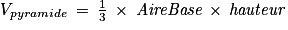
La base est le carré ABCD et son aire est égale à AB × BC = 4 × 4 = 16.
Ainsi :
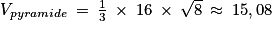
Donc le volume de la pyramide est d'environ 15 cm3.
Or le volume de cire dans un cuilleron plein est d'environ 32,7 cm3.
On a Vpyramide < VCui. Donc oui, un moule B peut recevoir une louche pleine de cire.
On a même : 2 × Vpyramide < VCui, donc avec une louche pleine, on pourrait verser de la cire dans deux moules B et il resterait encore de la cire dans le cuilleron.
4.
a.
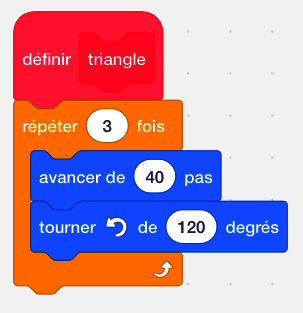 |
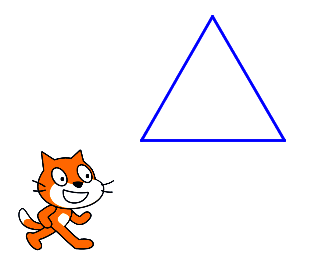 |
Le triangle comporte trois côtés, il faudra donc tracer trois segments (ici de longueur 40 pas).
La mesure d'angle à renseigner (le lutin est orienté « vers la droite ») est 180° − 60° = 120°.
En effet les angles dans un triangle équilatéral ont tous pour mesure 60°.
Ici le lutin regardant vers la droite, on peut assimiler cela à l'angle plat (de mesure 180°) et l'on souhaite qu'un angle de 60° soit tracé, il faut donc bien calculer : 180° − 60°.
La mesure d'angle à renseigner (le lutin est orienté « vers la droite ») est 180° − 60° = 120°.
En effet les angles dans un triangle équilatéral ont tous pour mesure 60°.
Ici le lutin regardant vers la droite, on peut assimiler cela à l'angle plat (de mesure 180°) et l'on souhaite qu'un angle de 60° soit tracé, il faut donc bien calculer : 180° − 60°.
b.
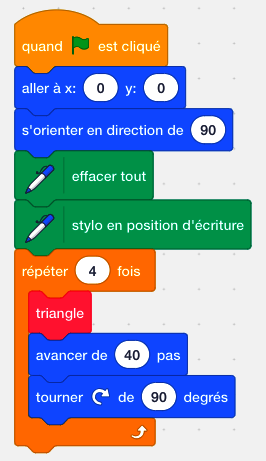 |
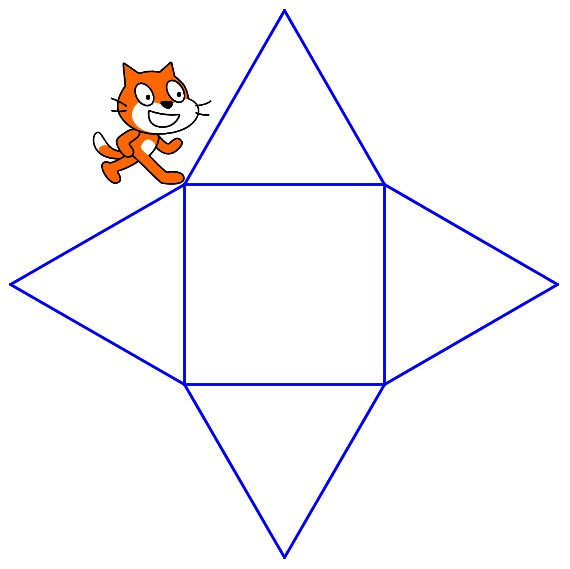 |
Le patron est composé de quatre triangles, on va donc inscrire l'entier 4 dans la ligne L3.
Les longueurs du carré sont de 4 cm, soit 40 pas. On va donc inscrire l'entier 40 dans la ligne L4.
Enfin, les angles dans un carré ont tous pour mesure 90°. Et comme 180° − 90° = 90°, alors on peut inscrire l'entier 90 dans la ligne L5.
On obtient bien le patron de la pyramide.
Les longueurs du carré sont de 4 cm, soit 40 pas. On va donc inscrire l'entier 40 dans la ligne L4.
Enfin, les angles dans un carré ont tous pour mesure 90°. Et comme 180° − 90° = 90°, alors on peut inscrire l'entier 90 dans la ligne L5.
On obtient bien le patron de la pyramide.
Des ressources Éduscol sur la programmation en langage Scratch sont disponibles, à télécharger ici (les pages 13 et 14 concernent le dessin de figures).
5.
a.
Dans la cellule B5 on peut inscrire la formule :
=SOMME(B2 :B4)
ou bien la formule :
=B2+B3+B4
Dans la cellule B5 on peut inscrire la formule :
=SOMME(B2 :B4)
ou bien la formule :
=B2+B3+B4
b.
Une ficelle de longueur de mèche 5 % plus grande est une ficelle dont la longueur de mèche a été augmentée de 5 %. Or augmenter un nombre positif (ici une longueur) de 5 % revient à multiplier ce nombre par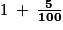 , c'est-à-dire par 1,05.
, c'est-à-dire par 1,05.
Dans la cellule D2 on peut ainsi inscrire la formule :
=(B2*3+C2*4)*1,05
Une ficelle de longueur de mèche 5 % plus grande est une ficelle dont la longueur de mèche a été augmentée de 5 %. Or augmenter un nombre positif (ici une longueur) de 5 % revient à multiplier ce nombre par
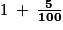 , c'est-à-dire par 1,05.
, c'est-à-dire par 1,05.Dans la cellule D2 on peut ainsi inscrire la formule :
=(B2*3+C2*4)*1,05
c.
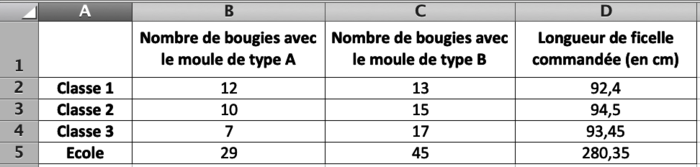 |
On calcule : ((12 + 10 + 7) × 3 + (13 + 15 + 17) × 4) × 1,05 = 280,35.
Ainsi, la directrice devrait commander 281 cm (2,81 cm) de ficelle.
Ainsi, la directrice devrait commander 281 cm (2,81 cm) de ficelle.
Des rappels sur l'utilisation d'un tableur peuvent être consultés si nécessaire ici.
Sujet corrigé réalisé par Jean Delautre, professeur de mathématiques au lycée Notre-Dame de la Paix à Lille.
Document précédent
Sujet 2025 de mathématiques, groupement académique 2 (nouveau)
Document suivant
Sujet 2024 de mathématiques, groupement académique 1
