Dernier essai le
- Score :
/20
Sujet
Sujet
Le sujet est composé de cinq exercices indépendants : ci-dessous sont traités les exercices 1 et 2.
Exercice 1
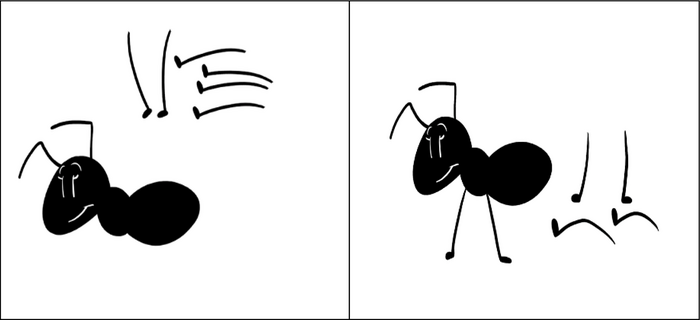
Un enseignant de grande section propose à ses élèves un jeu pour travailler la décomposition et la recomposition de nombres. Le jeu se compose de deux dés cubiques équilibrés et de corps de fourmis à compléter avec des pattes comme sur le dessin ci-dessous.
 |
Sur les six faces du premier dé sont inscrits les nombres suivants : 1 ; 1 ; 2 ; 3 ; 4 et 5.
Sur les six faces du deuxième dé sont inscrits les nombres suivants : 1 ; 2 ; 3 ; 4 ; 5 et 5. On donne à chaque élève un corps de fourmi et 6 pattes à fixer sur le corps.
Sur les six faces du deuxième dé sont inscrits les nombres suivants : 1 ; 2 ; 3 ; 4 ; 5 et 5. On donne à chaque élève un corps de fourmi et 6 pattes à fixer sur le corps.
Au début de la partie, chaque élève choisit un nombre compris entre 2 et 10. Ce nombre reste le même durant toute la partie. À tour de rôle, chaque élève joue. Il lance les deux dés :
La partie se termine lorsqu'un élève a gagné, en fixant les six pattes de sa fourmi.
- si la somme des nombres inscrits sur les faces supérieures des deux dés est égale au nombre choisi par cet élève, alors celui-ci fixe une patte à sa fourmi et relance les dés.
- sinon, c'est au joueur suivant de lancer les dés.
La partie se termine lorsqu'un élève a gagné, en fixant les six pattes de sa fourmi.
1.
Un élève choisit un nombre et lance les dés.a. Quelles sont les différentes sommes qu'il peut obtenir ?
b. Montrer que la probabilité qu'il obtienne 8 est égale à 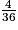
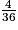
2.
Un autre élève choisit le nombre 6 et lance les dés.
a. Quelle est la probabilité qu'il gagne une patte pour sa fourmi dès son premier lancer ?
b. Quelle est la probabilité qu'il gagne deux pattes pour sa fourmi en 2 lancers ?
3.
Eden et Axelle commencent une partie. Eden choisit le nombre 6 et Axelle choisit un autre nombre.
a. Qui a le plus de chance de gagner la partie ? Justifier.
b. Eden est-il sûr de gagner la partie ? Justifier.
Exercice 2
Dans le cadre d'une liaison écoles-collège, une professeure d'EPS et une professeure des écoles organisent une course à vélo dont le parcours est composé de quatre tronçons en ligne droite.
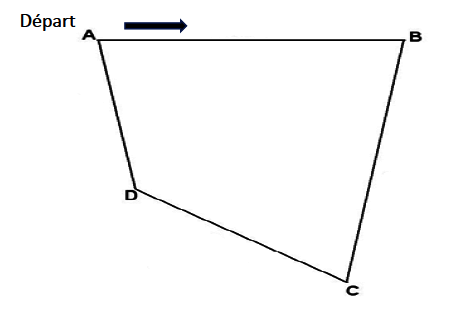
La figure ci-dessous représente le parcours et n'est pas à l'échelle. Les élèves partent du point A et tournent dans le sens des aiguilles d'une montre. Les dimensions sont les suivantes :
AB = 960 m, BC = 1,05 km, CD = 780 m et AD = 660 m.
La figure ci-dessous représente le parcours et n'est pas à l'échelle. Les élèves partent du point A et tournent dans le sens des aiguilles d'une montre. Les dimensions sont les suivantes :
AB = 960 m, BC = 1,05 km, CD = 780 m et AD = 660 m.
 |
1. Montrer que le parcours a pour longueur 3 450 m.
2.
Durant l'épreuve, Léo a réalisé, en 48 minutes, 2 tours complets et un tiers de tour du parcours.
a. Déterminer la distance parcourue par Léo.
b. Donner la vitesse moyenne de Léo en km/h.
c. En gardant la même vitesse moyenne, Léo aura-t-il parcouru 15 km en moins d'une heure et demie ? Justifier.
3. Une épreuve en relais est ensuite proposée. Tara parcourt les distances AB et BC à une vitesse moyenne de 10 km/h et Kevin parcourt les distances CD et DA à une vitesse moyenne de 6 km/h.
Quelle est la vitesse moyenne de ce binôme sur l'ensemble du parcours ? Justifier.
Quelle est la vitesse moyenne de ce binôme sur l'ensemble du parcours ? Justifier.
4.
a. La diagonale [BD] mesure 1,05 km. Représenter le parcours à l'échelle 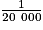
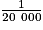
b. Amina a roulé à vélo pendant 25 minutes à une vitesse moyenne de 11,5 km/h.
Placer sur la figure tracée à la question 4.a. le point S à l'endroit où se trouve Amina au bout de sa course. Justifier.
Placer sur la figure tracée à la question 4.a. le point S à l'endroit où se trouve Amina au bout de sa course. Justifier.
Corrigé
Corrigé
Exercice 1
Construisons un tableau indiquant toutes les issues équiprobables de l'expérience qui consiste à lancer les deux dés et d'effectuer la somme des nombres inscrits sur les faces supérieures des deux dés :
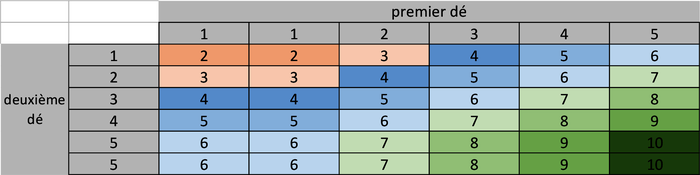 |
Le tableau ci-dessus permet en effet de calculer la probabilité d'obtenir chaque somme en calculant la fréquence à laquelle elle apparaît dans ce tableau.
 |
1.
a. Les neuf sommes qu'il peut obtenir sont : 2 — 3 — 4 — 5 — 6 — 7 — 8 — 9 — 10
b. Parmi les 36 issues équiprobables, 4 permettent d'obtenir une somme égale à 8 tableau ci-dessus) donc la probabilité d'obtenir 8 est égale à 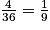 .
.
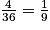 .
.2.
a. Parmi les 36 issues équiprobables, 8 permettent d'obtenir une somme égale à 6 (cf. tableau ci-dessus) donc la probabilité d'obtenir 8 est égale à 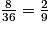 . L'élève a donc 2 chances sur 9 de gagner une patte de fourmi dès le premier tour.
. L'élève a donc 2 chances sur 9 de gagner une patte de fourmi dès le premier tour.
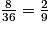 . L'élève a donc 2 chances sur 9 de gagner une patte de fourmi dès le premier tour.
. L'élève a donc 2 chances sur 9 de gagner une patte de fourmi dès le premier tour. b. Les deux lancers étants indépendants, la probabilité d'obtenir 8 à chacun des deux tours est égale à 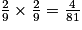 . L'élève a donc 4 chances sur 81 de gagner deux pattes de fourmi en deux lancers.
. L'élève a donc 4 chances sur 81 de gagner deux pattes de fourmi en deux lancers.
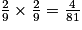 . L'élève a donc 4 chances sur 81 de gagner deux pattes de fourmi en deux lancers.
. L'élève a donc 4 chances sur 81 de gagner deux pattes de fourmi en deux lancers. 3.
a. Eden a choisi 6 qui est justement la somme qu'on a la plus grande probabilité d'obtenir en lançant les deux dés.
Donc Eden a le plus de chance de gagner.
Donc Eden a le plus de chance de gagner.
b. Pour autant, Eden n'est absolument pas sûr de gagner si les dés ne sont pas truqués : le résultat de chaque lancer reste aléatoire et rien n'assure qu'en lançant deux dés, Eden tombera une seule fois sur un des 8 cas sur 36 où la somme est égale à 8.
Exercice 2
1. La longueur parcourue est égale au périmètre du quadrilatère ABCD.
AB + BC + CD + DA = 960 m + 1 050 m + 780 m + 660 m = 3 450 m
AB + BC + CD + DA = 960 m + 1 050 m + 780 m + 660 m = 3 450 m
2.
a. Distance parcourue par Léo = 2 × 3 450 m + 3 450 m : 3 = 8 050 m
b. Léo a parcouru une distance d = 8 050 m = 8,05 km
en un temps t = 48 min =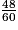 h = 0,8 h ;
h = 0,8 h ;
Sa vitesse moyenne en km/h est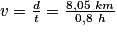 = 10,0625 km/h
= 10,0625 km/h
en un temps t = 48 min =
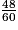 h = 0,8 h ;
h = 0,8 h ;Sa vitesse moyenne en km/h est
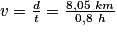 = 10,0625 km/h
= 10,0625 km/hc. En gardant cette même vitesse v = 10,0625 km/h, il aura parcouru 15 km pendant un temps t = 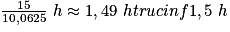 . Léo aura parcouru 15 km an moins d'une heure et demie en gardant la même vitesse moyenne.
. Léo aura parcouru 15 km an moins d'une heure et demie en gardant la même vitesse moyenne.
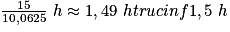 . Léo aura parcouru 15 km an moins d'une heure et demie en gardant la même vitesse moyenne.
. Léo aura parcouru 15 km an moins d'une heure et demie en gardant la même vitesse moyenne.3. Tara parcourt la distance AB + BC = 960 m + 1 050 m = 2 010 m = 2,01 km.
La vitesse moyenne de Tara étant de 10 km/h, elle parcourt ces 2,01 km en un temps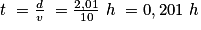
Kévin parcourt la distance CD + DA = 1,44 km
La vitesse moyenne de Kévin étant de 6 km/h, il parcourt ces 1,44 km en un temps
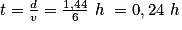
Le binôme parcourt donc 3,45 km en 0,201 h + 0,24 h = 0,441 h
Sa vitesse moyenne sur ce parcours d'un tour est donc de v =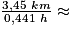 7,82 km/h
7,82 km/h
La vitesse moyenne de Tara étant de 10 km/h, elle parcourt ces 2,01 km en un temps
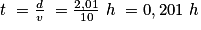
Kévin parcourt la distance CD + DA = 1,44 km
La vitesse moyenne de Kévin étant de 6 km/h, il parcourt ces 1,44 km en un temps
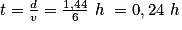
Le binôme parcourt donc 3,45 km en 0,201 h + 0,24 h = 0,441 h
Sa vitesse moyenne sur ce parcours d'un tour est donc de v =
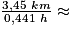 7,82 km/h
7,82 km/h4.
a. Sur un schéma à l'échelle 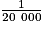 , chaque longueur réelle réduite 20 000 fois, donc 1 cm sur la schéma représente en réalité 20 000 cm = 200 m. Pour obtenir les longueurs en cm sur le schéma, on peut donc diviser par 200 les longueurs réelles en m ; on obtient :
, chaque longueur réelle réduite 20 000 fois, donc 1 cm sur la schéma représente en réalité 20 000 cm = 200 m. Pour obtenir les longueurs en cm sur le schéma, on peut donc diviser par 200 les longueurs réelles en m ; on obtient :
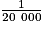 , chaque longueur réelle réduite 20 000 fois, donc 1 cm sur la schéma représente en réalité 20 000 cm = 200 m. Pour obtenir les longueurs en cm sur le schéma, on peut donc diviser par 200 les longueurs réelles en m ; on obtient :
, chaque longueur réelle réduite 20 000 fois, donc 1 cm sur la schéma représente en réalité 20 000 cm = 200 m. Pour obtenir les longueurs en cm sur le schéma, on peut donc diviser par 200 les longueurs réelles en m ; on obtient : | Longueur réelle en m | Longueur en cm sur schéma | |
| BD | 1 050 | 5,25 |
| AB | 960 | 4,8 |
| BC | 1 050 | 5,25 |
| CD | 780 | 3,9 |
| DA | 660 | 3,3 |
Pour construire le schéma, on peut commencer par tracer à la réglé graduée [BD], puis construire au compas et à la règle graduée les triangles BDA et BDC.
b. Amina a roulé 25 min = 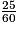 h à la vitesse de 11,5 km/h : elle a donc parcouru une distance d = v × t = 11,5 ×
h à la vitesse de 11,5 km/h : elle a donc parcouru une distance d = v × t = 11,5 × 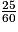 km
km  4 792 m.
4 792 m.
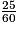 h à la vitesse de 11,5 km/h : elle a donc parcouru une distance d = v × t = 11,5 ×
h à la vitesse de 11,5 km/h : elle a donc parcouru une distance d = v × t = 11,5 × 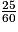 km
km  4 792 m.
4 792 m.Le parcours ayant une longueur de 3 450 m, elle en a déjà fait un tour, et ensuite parcourut AB (3 450 m + 960 m = 4 410 m) : il lui restera environ 4 792 m − 4 410 m à parcourir le long de [BC]. Au bout de 25 min, elle sera donc au point S de BC tel que BS  382 m.
382 m.
Sur le graphique BS = 382 : 200 1,9 cm
1,9 cm
 382 m.
382 m. Sur le graphique BS = 382 : 200
 1,9 cm
1,9 cm 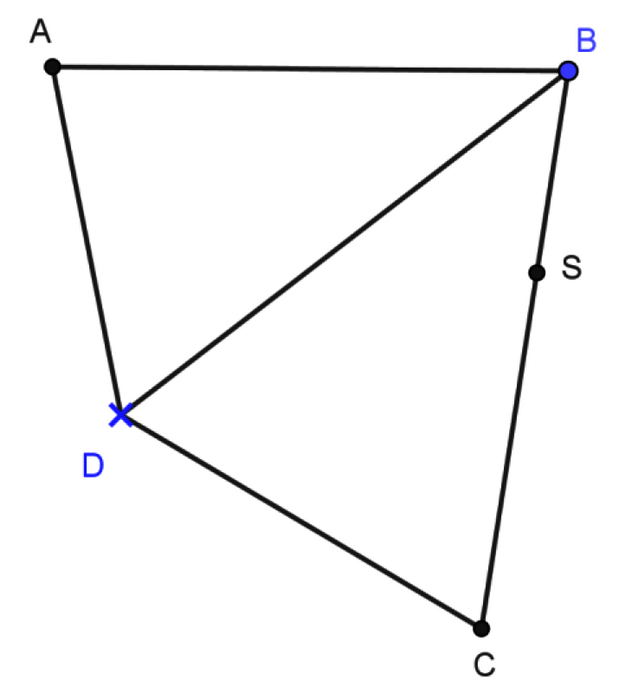 |
Document précédent
Sujet 2022 de mathématiques, groupement académique 2 — Exercices 3 et 4
