Dernier essai le
- Score :
/20
Sujet
Sujet
L'épreuve est notée sur 20. Une note globale égale ou inférieure à 5 est éliminatoire. Durée de l'épreuve : 3 h ; coefficient 1
Le sujet est composé de 5 exercices indépendants permettant de vérifier les connaissances du candidat.
Corrigé
Corrigé
Exercice 1
Partie A
1.
La longueur L de l'étiquette est égale au périmètre de base du cylindre de diamètre d = 8,4 cm, soit 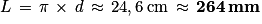 .
.
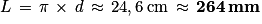 .
.Périmètre P d'un cercle de rayon r et de diamètre d
P = 2 × π × r = π × d
P = 2 × π × r = π × d
2.
On rappelle que :
Aire A d'un disque de rayon r
A = π × r2
A = π × r2
Le volume V du pluviomètre cylindrique de base de rayon r et de hauteur h est :
V = A × h = π × r2 × h
V = π × 4,2 × 4,2 × 15 = (264,6 × π) cm3 = (0,2646 × π) dm3 = (0,2646 × π) L
=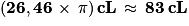
V = A × h = π × r2 × h
V = π × 4,2 × 4,2 × 15 = (264,6 × π) cm3 = (0,2646 × π) dm3 = (0,2646 × π) L
=
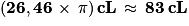
Seules les unités de capacités (L, dL, cL, etc.) sont enseignées à l'école primaire, mais il convient de connaître une de leurs correspondances avec les unités de volume, 1 dm3 = 1 L ou 1 m3 = 1 000 L pour en déduire le tableau ci-dessous :
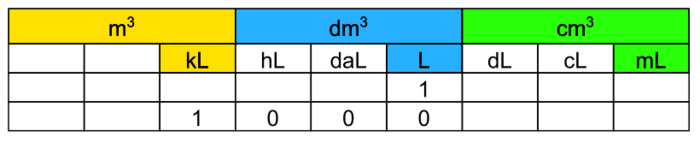 |
Attention : 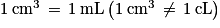 .
.
Le symbole du litre est L en majuscule… depuis 1979.
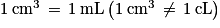 .
.Le symbole du litre est L en majuscule… depuis 1979.
3.
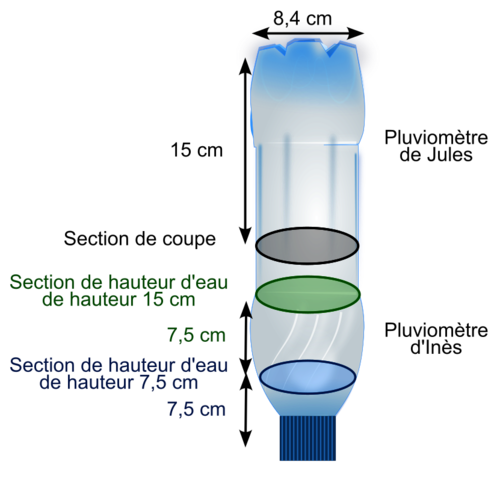
La courbe 1 correspond au pluviomètre d'Inès et la courbe 3 correspond à celui de Jules.
Justifications (non demandées) :
Justifications (non demandées) :
• Le pluviomètre de Jules est cylindrique : l'aire de sa base B est constante quelle que soit la hauteur h d'eau dans ce cylindre. Le volume d'eau en fonction de la hauteur h égal à B × h est donc proportionnel à h ; sa représentation graphique est donc une demi-droite passant par l'origine, soit la courbe 3.
• On remarque que jusqu'à 7,5 cm de hauteur d'eau environ (la moitié de 15 cm), le rayon de la section d'eau du pluviomètre d'Inès reste inférieur à 8,4 cm, puis augmente jusqu'à une hauteur d'eau d'au moins 15 cm : le volume d'eau versé entre 7,5 cm de hauteur et 15 cm de hauteur doit donc être supérieur au volume d'eau versé entre 0 et 7,5 cm de hauteur, ce qui n'est pas le cas sur la courbe 2 ; on en déduit que c'est la courbe 1 qui correspond au pluviomètre d'Inès.
 |
Lecture graphique sur la courbe 1
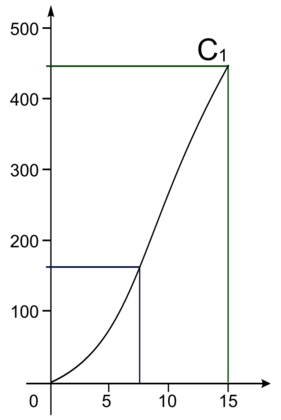 |
Pour une hauteur d'eau de 7,5 cm, le volume d'eau dans le pluviomètre est approximativement de 160 cm3.
Pour une hauteur d'eau de 15 cm, le volume d'eau dans le pluviomètre est approximativement de 450 cm3.
Donc entre 7,5 cm et 15 cm de hauteur, le volume d'eau versé est d'environ 290 cm3, bien supérieur à 160 cm3
Pour une hauteur d'eau de 15 cm, le volume d'eau dans le pluviomètre est approximativement de 450 cm3.
Donc entre 7,5 cm et 15 cm de hauteur, le volume d'eau versé est d'environ 290 cm3, bien supérieur à 160 cm3
Lecture graphique sur la courbe 2
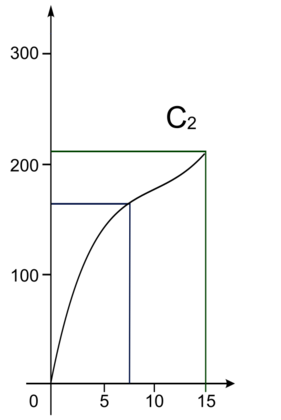 |
Pour une hauteur d'eau de 7,5 cm, le volume d'eau dans le pluviomètre est approximativement de 160 cm3.
Pour une hauteur d'eau de 15 cm, le volume d'eau dans le pluviomètre est approximativement de 215 cm3
Donc entre 7,5 cm et 15 cm de hauteur d'eau, le volume d'eau versé est d'environ 55 cm3, inférieur à 160 cm3, ce qui ne peut pas correspondre à la forme du pluviomètre d'Inès.
Pour une hauteur d'eau de 15 cm, le volume d'eau dans le pluviomètre est approximativement de 215 cm3
Donc entre 7,5 cm et 15 cm de hauteur d'eau, le volume d'eau versé est d'environ 55 cm3, inférieur à 160 cm3, ce qui ne peut pas correspondre à la forme du pluviomètre d'Inès.
Partie B
On peut consulter des cours et des exercices de statistiques de collège sur le site Euler des mathématiques de l'académie de Versailles https://euler-ressources.ac-versailles.fr/wims/>euler-ressources.ac-versailles.fr/wims
Pour la moyenne : euler-ressources.ac-versailles.fr
Pour la médiane : euler-ressources.ac-versailles.fr
Pour l'étendue : euler-ressources.ac-versailles.fr
Pour la moyenne : euler-ressources.ac-versailles.fr
Pour la médiane : euler-ressources.ac-versailles.fr
Pour l'étendue : euler-ressources.ac-versailles.fr
1. Calculons la moyenne des précipitations mensuelles en mm pendant les dix mois de l'année scolaire à Rennes :
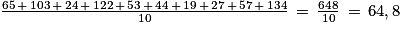
64,8 < 70,6
Par conséquent, c'est Lyon qui a connu les plus fortes précipitations mensuelles en moyenne durant les dix mois de l'année scolaire 2022-2023.
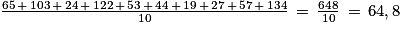
64,8 < 70,6
Par conséquent, c'est Lyon qui a connu les plus fortes précipitations mensuelles en moyenne durant les dix mois de l'année scolaire 2022-2023.
2.
Étendue des précipitations mensuelles à Rennes :
134 mm − 19 mm = 115 mm
Étendue des précipitations mensuelles à Lyon :
179 mm − 18 mm = 161 mm
L'étendue des précipitations à Lyon est supérieure à celle de Rennes.
134 mm − 19 mm = 115 mm
Étendue des précipitations mensuelles à Lyon :
179 mm − 18 mm = 161 mm
L'étendue des précipitations à Lyon est supérieure à celle de Rennes.
L'étendue correspond à la différence entre la valeur la plus élevée et la valeur la plus basse d'une série statistique.
3. L'affirmation est fausse (puisqu'elle n'est pas toujours vraie) :
Il ne faut pas confondre médiane et moyenne. Le contre-exemple ci-dessous pourrait correspondre aux relevés mensuels des précipitations à Lyon :
18 – 22 – 25 – 30 – 50 – 66 – 78 – 110 – 128 – 179
Il ne faut pas confondre médiane et moyenne. Le contre-exemple ci-dessous pourrait correspondre aux relevés mensuels des précipitations à Lyon :
18 – 22 – 25 – 30 – 50 – 66 – 78 – 110 – 128 – 179
La médiane est de 58 mm, la moyenne est de 70,6 mm et les hauteurs minimales et maximales sont de 18 mm et 179 mm, respectivement. Pourtant, dans cette série, les précipitations sont supérieures à 70,6 mm pendant seulement 4 mois.
Remarque : La médiane de 58 mm nous permet de conclure que :
« Dans la commune de Lyon, il y a 5 mois de l'année scolaire 2022-2023 sur 10 pendant lesquels les précipitations mensuelles ont été supérieures ou égales à 58 mm », mais la moyenne de 58 mm ne permet pas de conclure.
On peut par ailleurs constater qu'à Rennes, la moyenne est de 64,8 mm mais qu'il n'y a que 4 mois (et non 5) pendant lesquels les précipitations mensuelles ont été supérieures ou égales à 64,8 mm.
Exercice 2
On rappelle qu'en mathématiques une affirmation est soit vraie, soit fausse (elle n'est jamais parfois vraie !).
Pour justifier qu'une affirmation est fausse, on peut exhiber un contre-exemple (puisque ce n'est pas vrai sur cet exemple, l'affirmation est fausse).
En revanche, un ou de très nombreux exemples ne permettent pas de dire qu'une affirmation est vraie : il faut le démontrer dans le cas général.
Pour justifier qu'une affirmation est fausse, on peut exhiber un contre-exemple (puisque ce n'est pas vrai sur cet exemple, l'affirmation est fausse).
En revanche, un ou de très nombreux exemples ne permettent pas de dire qu'une affirmation est vraie : il faut le démontrer dans le cas général.
1.
L'affirmation 1 est vraie : le nombre décimal 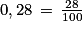 peut s'écrire sous la forme d'une fraction (quotient de deux entiers), donc c'est un nombre rationnel.
peut s'écrire sous la forme d'une fraction (quotient de deux entiers), donc c'est un nombre rationnel.
Remarque : on pouvait aussi argumenter que tout nombre décimal est rationnel.
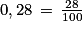 peut s'écrire sous la forme d'une fraction (quotient de deux entiers), donc c'est un nombre rationnel.
peut s'écrire sous la forme d'une fraction (quotient de deux entiers), donc c'est un nombre rationnel.Remarque : on pouvait aussi argumenter que tout nombre décimal est rationnel.
Rappel : un nombre rationnel peut s'écrire sous la forme d'une fraction, c'est-à-dire un quotient de deux entiers.
On retrouvera les définitions des différents types de nombres sur le document ressource du programme de cycle 3 « Fractions et nombres décimaux au cycle 3 » à partir de la page 3.
On retrouvera les définitions des différents types de nombres sur le document ressource du programme de cycle 3 « Fractions et nombres décimaux au cycle 3 » à partir de la page 3.
2. L'affirmation 2 est fausse, voici un contre-exemple :
Si a = 50 et b = 0,5, alors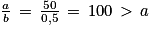
Si a = 50 et b = 0,5, alors
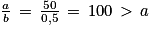
3.
L'affirmation 3 est vraie. Démontrons-le :
Soit n un entier naturel impair : puisque le reste de la division euclidienne de n par 2 est égal à 1, n peut s'écrire sous la forme 2q + 1, q étant le quotient entier de n par 2.
Soit n' un entier naturel impair : puisque le reste de la division euclidienne de n' par 2 est égal à 1, n' peut s'écrire sous la forme 2q' + 1, q' étant le quotient entier de n' par 2. On en déduit :
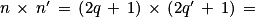
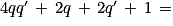
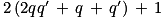 .
.
Le nombre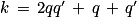 est un entier, car la somme et le produit de deux entiers sont des entiers.
est un entier, car la somme et le produit de deux entiers sont des entiers.
Ainsi, n × n' = 2 × k+ 1 est un nombre impair, puisque le reste de sa division euclidienne par 2 est égal à 1.
Soit n un entier naturel impair : puisque le reste de la division euclidienne de n par 2 est égal à 1, n peut s'écrire sous la forme 2q + 1, q étant le quotient entier de n par 2.
Soit n' un entier naturel impair : puisque le reste de la division euclidienne de n' par 2 est égal à 1, n' peut s'écrire sous la forme 2q' + 1, q' étant le quotient entier de n' par 2. On en déduit :
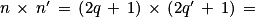
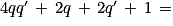
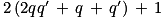 .
.Le nombre
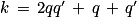 est un entier, car la somme et le produit de deux entiers sont des entiers.
est un entier, car la somme et le produit de deux entiers sont des entiers.Ainsi, n × n' = 2 × k+ 1 est un nombre impair, puisque le reste de sa division euclidienne par 2 est égal à 1.
Sur la division euclidienne, on peut consulter Sixième Cycle 3
4.
L'affirmation 4 est fausse : en effet la représentation graphique de la fonction affine f représentée passe par le point (0 ; 2), donc f(0) = 2.
Or 2 × 0 − 1,5 = −1,5, donc ce n'est pas la fonction f donnée qui est représentée.
On peut aussi remarquer que la fonction représentée est décroissante, alors que la fonction f donnée est croissante.
Or 2 × 0 − 1,5 = −1,5, donc ce n'est pas la fonction f donnée qui est représentée.
On peut aussi remarquer que la fonction représentée est décroissante, alors que la fonction f donnée est croissante.
Remarque : Ce n'est pas demandé, mais on peut déterminer la fonction affine 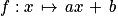 représentée, c'est-à-dire déterminer les nombres a et b.
représentée, c'est-à-dire déterminer les nombres a et b.
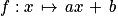 représentée, c'est-à-dire déterminer les nombres a et b.
représentée, c'est-à-dire déterminer les nombres a et b.La fonction affine f représentée passe par le point (0 ; 2) donc f(0) = 2.
La fonction affine f représentée passe par le point (1 ; 0,5) donc f(1) = 0,5.
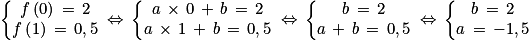
C'est la fonction affine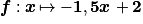 qui est représentée.
qui est représentée.
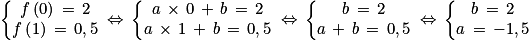
C'est la fonction affine
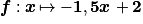 qui est représentée.
qui est représentée.On pourra consulter le cours sur les fonctions affines et s'exercer sur la correspondance avec leur représentation
5.
On suppose que les points B et C appartiennent au cercle (C1) et que les points D et E appartiennent au cercle (C2)
B et C appartiennent au cercle (C1) de centre A et de rayon 7,8 cm, par conséquent AB = AC = 7,8 cm.
D et E appartiennent au cercle (C2) de centre A et de rayon 2,4 cm, par conséquent AD = AE = 2,4 cm.
On en déduit que :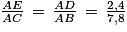 .
.
On sait que :
B et C appartiennent au cercle (C1) de centre A et de rayon 7,8 cm, par conséquent AB = AC = 7,8 cm.
D et E appartiennent au cercle (C2) de centre A et de rayon 2,4 cm, par conséquent AD = AE = 2,4 cm.
On en déduit que :
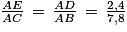 .
.On sait que :
• les points A, D et B sont alignés,
• les points A, E et C sont alignés dans le même ordre,
• les rapports 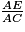 et
et 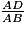 sont égaux.
sont égaux.
On en déduit, d'après la réciproque du théorème de Thalès, que les droites (DE) et (BC) sont parallèles.
Puisque les points A, D et B sont alignés ainsi que les points A, E et C, et que les droites (DE) et (BC) sont parallèles, on peut en déduire d'après le théorème de Thalès que :
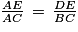 d'où
d'où 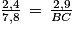 d'où
d'où 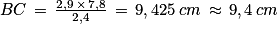 .
.
L'affirmation 5 est vraie.
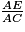 et
et 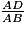 sont égaux.
sont égaux.On en déduit, d'après la réciproque du théorème de Thalès, que les droites (DE) et (BC) sont parallèles.
Puisque les points A, D et B sont alignés ainsi que les points A, E et C, et que les droites (DE) et (BC) sont parallèles, on peut en déduire d'après le théorème de Thalès que :
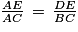 d'où
d'où 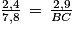 d'où
d'où 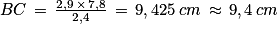 .
.L'affirmation 5 est vraie.
On pourra réviser la propriété (ou théorème) de Thalès et sa réciproque sur blogpeda.ac-bordeaux.fr/aromaths/
Exercice 3
Partie A
Les dés utilisés par les élèves sont assimilés à des cubes d'arête 19 mm (et non de côté, erreur dans l'énoncé).
Puisqu'on doit construire un patron à l'échelle 2, les 6 faces carrées auront sur le patron un côté de 2 × 19 mm = 38 mm.
Voici un exemple de patron :
Puisqu'on doit construire un patron à l'échelle 2, les 6 faces carrées auront sur le patron un côté de 2 × 19 mm = 38 mm.
Voici un exemple de patron :
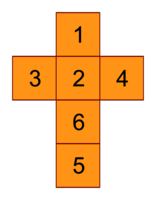 |
Partie B
On pourra consulter un manuel de 3e sur les probabilités au collège.
1. Puisque les faces des deux dés sont numérotées de 1 à 6 et qu'on considère la somme des deux faces supérieures, les résultats possibles sont tous les entiers compris entre 2 et 12.
2.
Cette expérience a 6 × 6 = 36 issues possibles équiprobables qu'on peut visualiser dans le tableau ci-dessous, où l'on peut s'imaginer disposer d'un dé rouge et d'un dé bleu.
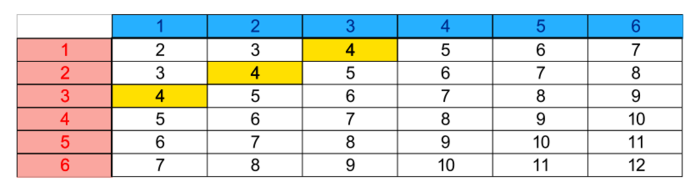 |
Une somme de 4 s'obtient :
• avec un 3 du dé bleu et un 1 du dé rouge,
• avec un 1 du dé bleu et un 3 du dé rouge,
• avec un 2 du dé bleu et un 2 du dé rouge.
On en déduit que la probabilité de l'événement : « La somme obtenue est égale à 4 » est de 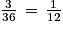 .
.
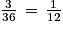 .
.3.
a. Le tableau permet de déterminer que c'est la somme 7 qui a la plus grande probabilité d'apparaître.
b. La probabilité d'obtenir une somme de 7 est égale à 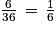 .
.
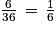 .
.Partie C
On considère à présent l'écart entre les deux nombres obtenus sur les faces supérieures : cette expérience a 6 × 6 = 36 issues possibles équiprobables qu'on peut visualiser dans le tableau ci-dessous, où l'on peut s'imaginer disposer d'un dé rouge et d'un dé bleu.
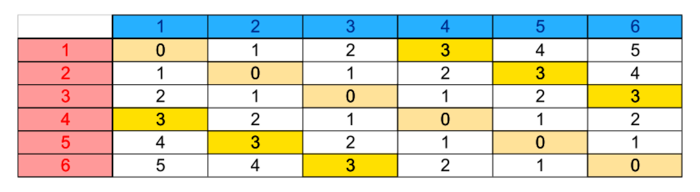 |
Dans ce contexte, deux événements ont une probabilité égale à 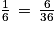 :
:
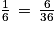 :
:• l'événement « Obtenir un écart égal à 0 »,
• l'événement « Obtenir un écart égal à 3 ».
Exercice 4
Partie A
1.
a. L'enseignante ayant disposé huit plots équidistants tout au long de la piste de 200 m, la distance entre deux plots est de 200 ÷ 8 = 25 m. Comme Lola a aussi parcouru 4 tours complets, sa distance parcourue est de 200 × 4 + 25 = 825 m.
b. Lola a parcouru 825 mètres en 5 minutes, sa vitesse moyenne est donc : 825 ÷ 5 = 165 m/min.
2. Joris a parcouru 700 mètres en 5 minutes.
Sa vitesse moyenne est donc : 700 ÷ 5 = 140 m/min.
140 × 60 = 8 400 m, soit 8,4 km en 60 minutes, c'est-à-dire en 1 h. La vitesse moyenne de Joris est donc de 8,4 km/h.
Sa vitesse moyenne est donc : 700 ÷ 5 = 140 m/min.
140 × 60 = 8 400 m, soit 8,4 km en 60 minutes, c'est-à-dire en 1 h. La vitesse moyenne de Joris est donc de 8,4 km/h.
3. Lola a parcouru 825 − 700 = 125 m de plus que Joris, soit :· 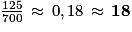 % de plus que Joris.
% de plus que Joris.
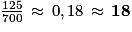 % de plus que Joris.
% de plus que Joris.Partie B
Vous devez savoir utiliser les fonctions habituelles d'un tableur (voir par exemple les exercices sur https://clg-monnet-briis.ac-versailles.fr/Utiliser-un-tableur ou sur https://euler-ressources.ac-versailles.fr/), ce qui vous permettra aussi de cerner la notion de variable, comme précisé dans le document « Utiliser le calcul littéral » sur https://eduscol.education.fr/document/17263/download : « L'utilisation du tableur peut faciliter la compréhension de la notion de variable dans la mesure où, dans l'édition d'une formule, ce sont les adresses des cellules (et non leur contenu) qui sont prises en compte. La modification du contenu d'une cellule désignée dans une formule modifie le contenu de la cellule où est implantée la formule, ce qui permet d'appréhender les notions de variable et de fonction. »
1.
Une formule pouvant être saisie dans la cellule D2 puis recopiée vers le bas pour obtenir le tableau complété est :
=200*B2+25*C2
=200*B2+25*C2
Ne pas oublier le signe = pour débuter une formule sur un tableur.
2. Lorsqu'on connaît le nombre x de mètres parcourus en 5 minutes, on peut en déduire que l'élève a parcouru en moyenne 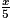 mètres en 1 min.
mètres en 1 min.
En 1 heure, il aura donc parcouru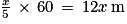 , soit
, soit 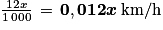 .
.
Une formule qui peut être saisie dans la cellule E2 puis recopiée vers le bas pour obtenir le tableau complété est :
=0,012*D2
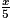 mètres en 1 min.
mètres en 1 min.En 1 heure, il aura donc parcouru
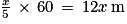 , soit
, soit 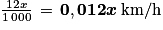 .
.Une formule qui peut être saisie dans la cellule E2 puis recopiée vers le bas pour obtenir le tableau complété est :
=0,012*D2
3. 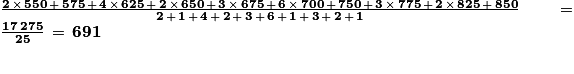
La distance moyenne parcourue par les élèves de cette classe est de 691 m.
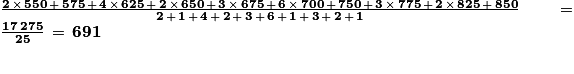
La distance moyenne parcourue par les élèves de cette classe est de 691 m.
Partie C
1.
Soient L la longueur du rectangle et l sa largeur, exprimées en mètres.
a. Puisque 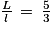 ,
, 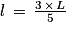 ; donc si L = 20 m,
; donc si L = 20 m, 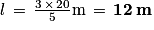 .
.
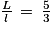 ,
, 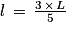 ; donc si L = 20 m,
; donc si L = 20 m, 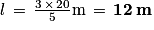 .
.b. Sachant que le périmètre d'un cercle de diamètre d est égal à π × d, la longueur de la piste en mètres est :
2 × L + π × l.
Puisque l = 12 m et L = 20 m, la longueur de la piste est égale à :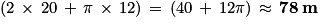 .
.
2 × L + π × l.
Puisque l = 12 m et L = 20 m, la longueur de la piste est égale à :
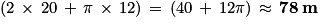 .
.2.
Si la piste a une longueur totale de 200 m et si L est la longueur et l la largeur du rectangle en mètres, alors :
2 × L + π × l = 200
On en déduit :
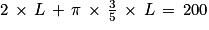
D'où :
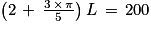
Soit :
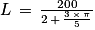
Donc :
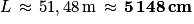
Et :
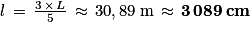
2 × L + π × l = 200
On en déduit :
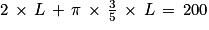
D'où :
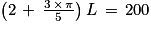
Soit :
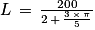
Donc :
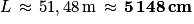
Et :
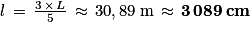
Exercice 5
Partie A
1.
Poursuivons par schématisation la construction de l'élève :
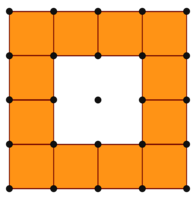 |
On voit que l'élève doit construire 12 carrés.
En effet, sur un géoplan de 25 picots, il y a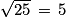 picots (par exemple P1, P2, P3, P4 et P5) sur chaque côté du carré délimitant le géoplan.
picots (par exemple P1, P2, P3, P4 et P5) sur chaque côté du carré délimitant le géoplan.
En effet, sur un géoplan de 25 picots, il y a
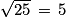 picots (par exemple P1, P2, P3, P4 et P5) sur chaque côté du carré délimitant le géoplan.
picots (par exemple P1, P2, P3, P4 et P5) sur chaque côté du carré délimitant le géoplan.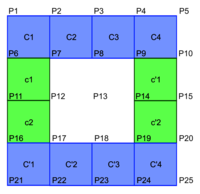 |
L'élève devra construire 5 − 1 = 4 carrés sur chaque côté horizontal du géoplan et 4 − 2 = 2 carrés sur chaque côté vertical (il ne faut en effet pas compter deux fois les « carrés des coins » du géoplan).
Soit en tout 2 × 4 + 2 × (4 − 2) = 8 + 4 = 12 carrés.
Soit en tout 2 × 4 + 2 × (4 − 2) = 8 + 4 = 12 carrés.
2. En utilisant un raisonnement analogue, avec un géoplan de 81 picots soit 9² picots, il faudra construire un nombre de carrés égal à :
2 × (9 − 1) + 2 × (9 − 1 − 2) = 16 + 12 = 28 carrés.
2 × (9 − 1) + 2 × (9 − 1 − 2) = 16 + 12 = 28 carrés.
3. Pour un géoplan de n² picots (n > 2), il faudra construire :
2 × (n − 1) + 2 × (n − 1 − 2) = 2n − 2 + 2(n − 3) = 2n − 2 + 2n − 6 = 4n − 8.
2 × (n − 1) + 2 × (n − 1 − 2) = 2n − 2 + 2(n − 3) = 2n − 2 + 2n − 6 = 4n − 8.
4. On ne peut pas utiliser tous les élastiques. En effet, n étant un entier naturel, 4n − 8 = 4(n − 2) est un nombre multiple de 4, donc différent de 107.
De même, on ne peut utiliser ni 106 élastiques ni 105 élastiques, puisque ces deux nombres ne sont pas des multiples de 4. En revanche, on peut utiliser 104 élastiques, puis déterminer n tel que 4n − 8 = 104, soit :
4n = 104 + 8 = 112 donc n = 112 ÷ 4 = 28.
Le nombre de picots du géoplan est donc égal à n2 = 784 picots.
De même, on ne peut utiliser ni 106 élastiques ni 105 élastiques, puisque ces deux nombres ne sont pas des multiples de 4. En revanche, on peut utiliser 104 élastiques, puis déterminer n tel que 4n − 8 = 104, soit :
4n = 104 + 8 = 112 donc n = 112 ÷ 4 = 28.
Le nombre de picots du géoplan est donc égal à n2 = 784 picots.
Partie B
1.
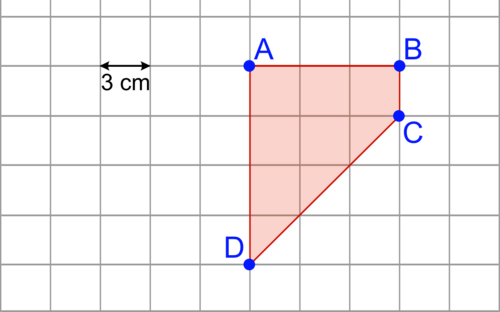 |
2.
Considérons le point E, tel que ABCE soit un rectangle et donc ECD un triangle rectangle en E :
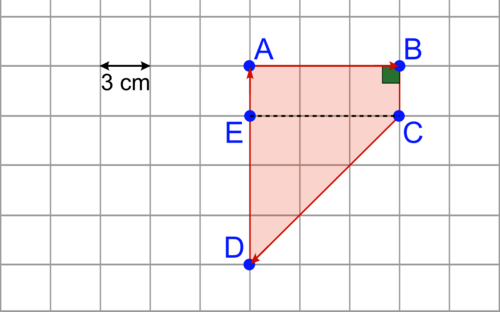 |
a. Aire de ABCD = aire de ABCE + aire de ECD
Aire de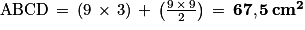 .
.
Aire de
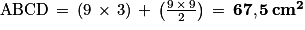 .
.b.
Calculons la longueur du segment [CD] : le triangle DEC étant rectangle en E, d'après le théorème de Pythagore :
DC² = DE + EC²
Soit DC² = 9² + 9² = 2 × 9² donc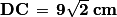 .
.
DC² = DE + EC²
Soit DC² = 9² + 9² = 2 × 9² donc
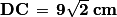 .
.Propriété de Pythagore (permettant de calculer la longueur d'un côté d'un triangle rectangle quand on connaît la longueur de ses deux autres côtés).
Si un triangle est rectangle, alors le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Si un triangle est rectangle, alors le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Périmètre de ABCD = AB + BC + CD + DA
Périmètre de ABCD = 9 + 3 +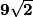 + 12
+ 12
Périmètre de ABCD = 24 +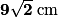
Périmètre de ABCD = 9 + 3 +
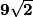 + 12
+ 12Périmètre de ABCD = 24 +
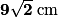
3.
Il est nécessaire, avant de se présenter au CRPE, de s'entraîner à la programmation, si possible avec Scratch (en ligne https://scratch.mit.edu/download/scratch2) dont vous remarquerez dans l'adresse qu'il a été développé par le MIT (pour les enfants).
On pourra consulter le document ressource « Algorithme et programmation » des programmes du cycle 4.
On pourra consulter le document ressource « Algorithme et programmation » des programmes du cycle 4.
Figure à tracer :
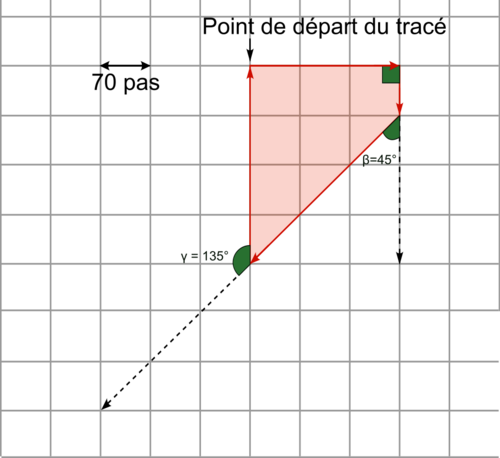 |
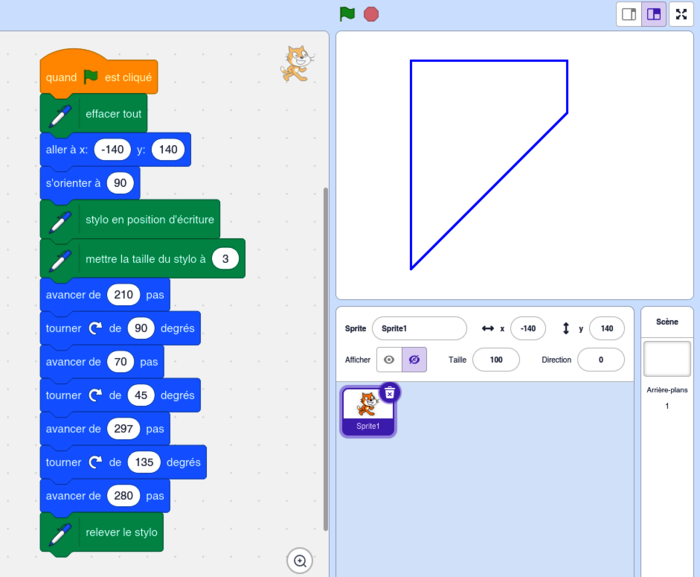
Voici ce que cela donne en couleurs, pour faciliter vos essais sur Scratch :
*Dans cette figure DE = EC = 3 × 70 pas = 210 pas. Par conséquent, avec un raisonnement analogue à la question 2. a. : DC² = 2 × 210² puis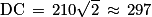 pas.
pas.
On obtient :
| L'exécution du programme débute lorsqu'on clique sur le drapeau vert | |
| Efface la partie de l'écran où est construite la figure | ||
| Le curseur va au point de coordonnées (−140 ; 140) de cet écran | ||
| S'oriente pour tracer un segment horizontal de gauche à droite | ||
| Le stylo écrira lors des déplacements | ||
| Réglage de l'épaisseur du tracé du crayon | ||
| Avance de 210 pas = 3 × 70 pas, traçant un segment horizontal | ||
| Tourne de 90° dans le sens des aiguilles d'une montre | ||
| Trace un segment vertical de 70 pas de haut en bas | ||
| Tourne de 45° dans le sens des aiguilles d'une montre, donc A = 45 | ||
Trace un segment oblique de 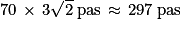 , donc B = 297* , donc B = 297* | ||
| Tourne de 135° dans le sens des aiguilles d'une montre, donc C = 135 | ||
| Trace un segment vertical de bas en haut de 280 pas | ||
| Relève le stylo pour les prochains déplacements |
*Dans cette figure DE = EC = 3 × 70 pas = 210 pas. Par conséquent, avec un raisonnement analogue à la question 2. a. : DC² = 2 × 210² puis
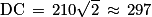 pas.
pas.On obtient :
 |
Sujet corrigé réalisé par Hélène Radzynski, professeure agrégée de mathématiques, ancienne formatrice de professeurs des écoles en mathématiques.
Document suivant
Sujet 2024 de mathématiques, groupement académique 2