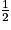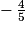Dernier essai le
- Score :
/20
En quoi consiste ce type de tests ?
• Dans les tests de raisonnement numérique, il s'agit :
- de résoudre des problèmes ;
- de réaliser des calculs de proportionnalité, de pourcentage, de TVA, de durée, de vitesse, etc. ;
- de calculer les surfaces et les volumes de formes géométriques simples ou associées (rectangle, carré, triangle, parallélogramme, trapèze, cube, parallélépipède, disque, sphère, etc.) ;
- de résoudre des équations du second degré.
• Un problème n'exige pas toujours un calcul numérique. Il peut privilégier l'esprit de déduction et une bonne logique. Il est donc important de lire attentivement les énoncés et de prendre le temps de la réflexion avant de se lancer dans des calculs complexes.
• Il faut aussi être rapide sans l'aide de la calculatrice.
Comment s'y préparer ?
• Revoir les diverses formules de calcul des aires et volumes.
• Mémoriser formules et définitions.
• S'exercer régulièrement et tirer profit des situations du quotidien, par exemple en recalculant la TVA sur les factures.
Astuces et rappels
• Le périmètre est une longueur dont l'unité principale est le mètre.
Calcul du périmètre
Périmètre d'un rectangle = 2 × (longueur + largeur).
Périmètre d'un carré = 4 × côté.
Périmètre d'un cercle = 2 π × rayon ou π × diamètre (π (pi) = 3,1416).
Calcul du périmètre
Périmètre d'un rectangle = 2 × (longueur + largeur).
Périmètre d'un carré = 4 × côté.
Périmètre d'un cercle = 2 π × rayon ou π × diamètre (π (pi) = 3,1416).
• La surface ou aire a pour unité principale le mètre carré.
Calcul de la surface
Surface d'un rectangle = longueur × largeur.
Surface d'un carré = côté × côté.
Surface d'un parallélogramme = base × hauteur.
Surface d'un trapèze =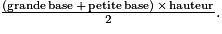
Surface d'un triangle =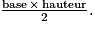
Surface d'un cercle = π × (rayon)2.
Calcul de la surface
Surface d'un rectangle = longueur × largeur.
Surface d'un carré = côté × côté.
Surface d'un parallélogramme = base × hauteur.
Surface d'un trapèze =
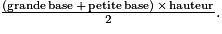
Surface d'un triangle =
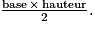
Surface d'un cercle = π × (rayon)2.
• Le volume a pour unité principale le mètre cube.
Calcul du volume
Volume d'un cube = (côté)3.
Volume d'un parallélépipède rectangle de cotés a, b, c = a × b × c.
Volume d'une sphère =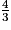 π × (rayon)3.
π × (rayon)3.
Volume d'un cylindre = π × (rayon)2 × hauteur.
Volume d'un cône =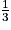 × π × (rayon)2 × hauteur.
× π × (rayon)2 × hauteur.
Volume d'une pyramide =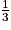 × aire de la base × hauteur.
× aire de la base × hauteur.
Calcul du volume
Volume d'un cube = (côté)3.
Volume d'un parallélépipède rectangle de cotés a, b, c = a × b × c.
Volume d'une sphère =
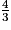 π × (rayon)3.
π × (rayon)3.Volume d'un cylindre = π × (rayon)2 × hauteur.
Volume d'un cône =
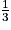 × π × (rayon)2 × hauteur.
× π × (rayon)2 × hauteur.Volume d'une pyramide =
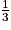 × aire de la base × hauteur.
× aire de la base × hauteur.• Vitesse
Formule : vitesse moyenne V sur une distance parcourue d pendant une durée t :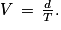
Mais aussi : d = V × t et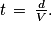
Formule : vitesse moyenne V sur une distance parcourue d pendant une durée t :
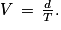
Mais aussi : d = V × t et
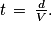
• Grandeurs proportionnelles
Deux grandeurs sont proportionnelles si l'une devient 2, 3, … fois plus grande (ou plus petite) quand l'autre devient 2, 3, … fois plus grande (ou plus petite).
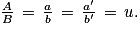
Deux grandeurs sont proportionnelles si l'une devient 2, 3, … fois plus grande (ou plus petite) quand l'autre devient 2, 3, … fois plus grande (ou plus petite).
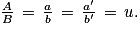
• Identités remarquables
(a + b)2 = a2 + 2ab + b2.
(a − b)2 = a2 − 2ab + b2.
(a + b)(a − b) = a2 − b2.
(a + b)2 = a2 + 2ab + b2.
(a − b)2 = a2 − 2ab + b2.
(a + b)(a − b) = a2 − b2.
• Pourcentage
Calcul du pourcentage d'une quantité N
x % de N = N ×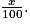
Calcul du pourcentage d'une quantité N
x % de N = N ×
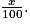
Question 1
Julie dessine un petit cercle de 16 cm de rayon à l'intérieur d'un plus grand disque de 38 cm de rayon. Elle veut peindre l'espace compris entre ces deux disques.
Calculer la surface qu'elle va colorier.
Calculer la surface qu'elle va colorier.
Écrivez la réponse dans la zone colorée.
Julie va colorier cm2.
Aire du petit cercle = π × (rayon)2 = π × 162 = 3,14 × 256 = 803,84 cm2.
Aire du grand cercle = π × (rayon)2 = π × 382 = 3,14 × 1 444 = 4 534,16 cm2.
Calcul de l'espace compris entre les deux disques : Aire du grand cercle − Aire du petit cercle = 4 534,16 − 803,84 = 3 730,32 cm2.
Aire du grand cercle = π × (rayon)2 = π × 382 = 3,14 × 1 444 = 4 534,16 cm2.
Calcul de l'espace compris entre les deux disques : Aire du grand cercle − Aire du petit cercle = 4 534,16 − 803,84 = 3 730,32 cm2.
Question 2
On taille dans un morceau de bois un cylindre de 12 cm de diamètre et de 18 cm de hauteur.
Quel est le volume du cylindre en fonction de π ?
Quel est le volume du cylindre en fonction de π ?
Cochez la bonne réponse.
| ||
| ||
|
Volume du cylindre = π × (rayon)2 × hauteur.
Calcul du rayon :
d = 2 × r
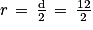 = 6 cm.
= 6 cm.
d = 2 × r
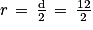 = 6 cm.
= 6 cm.Volume du cylindre = π × (rayon)2 × hauteur = π × 62 × 18 = 648 π cm3.
Question 3
Benoît part de Rennes à 8 h 12 et arrive à Paris à 11 h 45.
Quelle a été la durée de son voyage ?
Quelle a été la durée de son voyage ?
Cochez la bonne réponse.
| ||
| ||
|
11 h 45 − 8 h 12 = 3 h 33.
Question 4
Un potier vend des bols en faïence sur les marchés de Noël.
Sur le premier marché, il vend 22 bols.
Sur le deuxième marché, il vend 20 bols.
Sur le troisième marché, il vend 29 bols.
Sur le quatrième marché, il vend 25 bols.
Quel est le pourcentage de bols vendus lors du dernier marché ?
Sur le premier marché, il vend 22 bols.
Sur le deuxième marché, il vend 20 bols.
Sur le troisième marché, il vend 29 bols.
Sur le quatrième marché, il vend 25 bols.
Quel est le pourcentage de bols vendus lors du dernier marché ?
Cochez la bonne réponse.
| ||
| ||
|
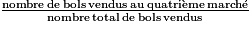 × 100
× 100=
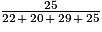 × 100
× 100=
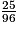 × 100
× 100= 0,26 × 100
= 26 %.
Question 5
Vous souhaitez assister à un concert. Au tarif plein, le billet coûte 40 €, mais vous bénéficiez d'une réduction de 30 %.
Combien allez-vous payer votre billet ?
Combien allez-vous payer votre billet ?
Écrivez la réponse dans la zone colorée.
Vous allez payer €.
Calcul du montant de la réduction : 30 % de 40 € = 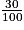 × 40 = 0,3 × 40 = 12 €.
× 40 = 0,3 × 40 = 12 €.
La place à tarif réduit coûte 40 € − 12 € = 28 €.
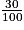 × 40 = 0,3 × 40 = 12 €.
× 40 = 0,3 × 40 = 12 €.La place à tarif réduit coûte 40 € − 12 € = 28 €.
Question 6
Un randonneur a parcouru 15 km en 1 heure, soit plus de 4 m à la seconde.
Cette affirmation est-elle vraie ou fausse ?
Cette affirmation est-elle vraie ou fausse ?
Cochez la bonne réponse.
| ||
|
En 1 heure, il a parcouru 15 000 m.
1 heure équivaut à 3 600 secondes.
Donc sa vitesse à la seconde est égale à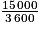 , soit 4,16 m/ s.
, soit 4,16 m/ s.
1 heure équivaut à 3 600 secondes.
Donc sa vitesse à la seconde est égale à
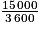 , soit 4,16 m/ s.
, soit 4,16 m/ s.Question 7
Une veste est vendue 96 € TTC.
Quel est son prix hors taxe, sachant que le taux de TVA est de 19,6 % ? (arrondir aux centimes)
Quel est son prix hors taxe, sachant que le taux de TVA est de 19,6 % ? (arrondir aux centimes)
Écrivez la réponse dans la zone colorée.
Son prix hors taxe est de €.
La TVA (taxe sur la valeur ajoutée), ici d'un pourcentage de 19,6 %, s'ajoute au prix HT (hors taxe) pour donner le prix TTC (toutes taxes comprises).
Prix TTC = prix HT + (prix HT ×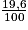 ) ou pTTC = pHT (1 +
) ou pTTC = pHT (1 + 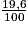 ),
),
soit 96 € = pHT (1 +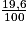 ),
),
pHT =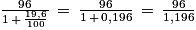 = 80,26 €.
= 80,26 €.
Prix TTC = prix HT + (prix HT ×
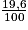 ) ou pTTC = pHT (1 +
) ou pTTC = pHT (1 + 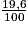 ),
), soit 96 € = pHT (1 +
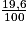 ),
),pHT =
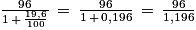 = 80,26 €.
= 80,26 €.Question 8
Un sac coûte 100 €. À la rentrée, on augmente son prix de 20 %, puis on le réduit de 20 % au moment des soldes.
Quel est son prix soldé ?
Quel est son prix soldé ?
Cochez la bonne réponse.
| ||
| ||
|
Calcul de l'augmentation de 20 % :
100 € ×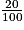 = 20 €.
= 20 €.
Le prix après augmentation est de 120 €.
100 € ×
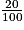 = 20 €.
= 20 €.Le prix après augmentation est de 120 €.
Calcul de la réduction de 20 % :
120 € ×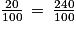 = 24 €.
= 24 €.
120 € ×
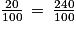 = 24 €.
= 24 €.Calcul du prix soldé :
120 € − 24 € = 96 €.
Attention au piège, il ne faut pas additionner ou soustraire des pourcentages.
120 € − 24 € = 96 €.
Attention au piège, il ne faut pas additionner ou soustraire des pourcentages.
Question 9
Quel résultat correspond à l'expression suivante ?
A = (3x + 2)2 − (5 − 2x)(3x + 2)
A = (3x + 2)2 − (5 − 2x)(3x + 2)
Cochez la bonne réponse.
| ||
| ||
|
Il s'agit de développer en utilisant l'identité remarquable (a + b)2 = a2 + 2ab + b2.
A = (3x + 2)2 − (5 − 2x)(3x + 2)
A = [(3x)2 + 2 × 2 × 3x + 22] − [(5 × 3x + 5 × 2 − 2x × 3x − 2x × 2)]
A = [9x2 + 12x + 4] − [15x + 10 − 6 x2 − 4x]
A = 9x2 + 12x + 4 − 15x − 10 + 6x2 + 4x
A = 15x2 + x − 6.
A = (3x + 2)2 − (5 − 2x)(3x + 2)
A = [(3x)2 + 2 × 2 × 3x + 22] − [(5 × 3x + 5 × 2 − 2x × 3x − 2x × 2)]
A = [9x2 + 12x + 4] − [15x + 10 − 6 x2 − 4x]
A = 9x2 + 12x + 4 − 15x − 10 + 6x2 + 4x
A = 15x2 + x − 6.
Question 10
Factoriser l'expression A = (2x − 1)2 + (2x − 1)(3x + 5).
Puis résoudre l'équation A = 0.
Quel est le bon résultat ?
Puis résoudre l'équation A = 0.
Quel est le bon résultat ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
|
Les deux réponses sont justes.
Factorisation :
On remarque qu'il existe un facteur commun (2x − 1).
A = (2x − 1)2 + (2x − 1)(3x + 5)
A = (2x − 1)(2x − 1) + (2x − 1)(3x + 5)
A = (2x − 1) [(2x − 1) + (3x + 5)]
A = (2x − 1) [2x − 1 + 3x + 5]
A = (2x − 1)(5x + 4).
On remarque qu'il existe un facteur commun (2x − 1).
A = (2x − 1)2 + (2x − 1)(3x + 5)
A = (2x − 1)(2x − 1) + (2x − 1)(3x + 5)
A = (2x − 1) [(2x − 1) + (3x + 5)]
A = (2x − 1) [2x − 1 + 3x + 5]
A = (2x − 1)(5x + 4).
Résolution de l'équation (2x − 1)(5x + 4) = 0 :
Pour qu'un produit de facteurs soit nul, il suffit qu'un seul des facteurs soit nul.
Soit :
2x − 1 = 0
2x = 1
x =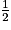 .
.
Soit :
5x + 4 = 0
5x = − 4
x =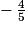 .
.
Pour qu'un produit de facteurs soit nul, il suffit qu'un seul des facteurs soit nul.
Soit :
2x − 1 = 0
2x = 1
x =
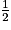 .
.Soit :
5x + 4 = 0
5x = − 4
x =
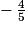 .
.
Document précédent
Calculs numériques