Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (4 points)
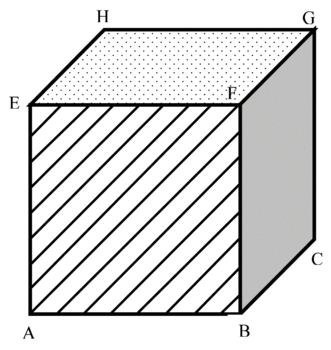
La figure 1 suivante représente un cube en bois ABCDHEFG dont les faces opposées sont décorées avec le même motif : hachures, points ou uni.
 |
Le volume de ce cube est 216 cm3.
1) Nommer chaque face cachée de ce cube et indiquer son motif.
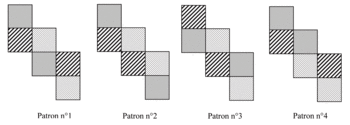
2) Parmi les patrons suivants quels sont ceux qui correspondent au cube ABCDHEFG ? Justifier la réponse.
 |
3) Le cube ABCDHEFG est scié en petits cubes identiques dont les arêtes sont 3 fois plus petites que celles du cube ABCDHEFG (cf. figure 2).
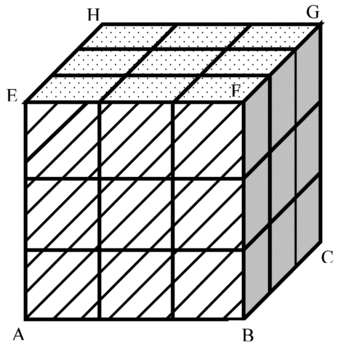 |
a. Combien de petits cubes obtient-on ?
b. Déterminer le volume d'un petit cube.
c. En déduire la longueur des arêtes d'un petit cube et du grand cube ABCDHEFG.
d. Ces petits cubes n'ont pas tous le même nombre de faces décorées. Reproduire et compléter le tableau suivant qui compte les cubes ayant le même nombre de faces décorées.
| Nombre de faces décorées | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Nombre de petits cubes | | | | | | | |
e. Quel est le nombre total de petites faces décorées ?
4) Par assemblage et collage, on reconstitue le gros cube initial auquel on retire un petit cube à chacun de ses 8 sommets ; on obtient ainsi un nouveau solide.
a. Calculer le volume de ce solide.
b. Calculer son aire.
Exercice 2 (4 points)
Deux villes A et B se situent du même côté d'une voie ferrée rectiligne (CD), comme l'indique le schéma suivant.
On cherche où construire une gare G pour que le trajet de la ville A à la ville B en passant par la gare G soit le plus court possible.
On cherche où construire une gare G pour que le trajet de la ville A à la ville B en passant par la gare G soit le plus court possible.
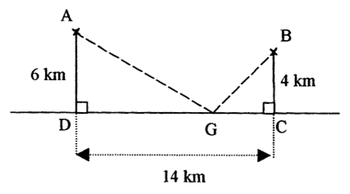 |
1) Représenter les points A, B, C et D sur une figure pour laquelle 1 cm correspond à 1 km. Quelle est l'échelle de cette représentation ? Justifier la réponse.
2) Construire le point E symétrique du point B par rapport à la droite (CD).
3) On appelle F le point d'intersection des droites (AE) et (CD).
Soit M un point quelconque du segment [DC] distinct du point F.
Démontrer que AM + MB > AF + FB.
Soit M un point quelconque du segment [DC] distinct du point F.
Démontrer que AM + MB > AF + FB.
4) En déduire l'endroit où l'on doit construire la gare G.
5) Démontrer que : 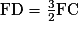 .
.
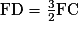 .
.6) En déduire que FC = 5,6 km.
7) Calculer, au mètre près, la longueur du trajet de la ville A à la ville B en passant par la gare G.
Question complémentaire : Étude des documents 1 et 2 de l'annexe 1 (5 points)
1) On considère d'abord le document 1.
a. Décrire deux procédures possibles des élèves en réponse à la question 1.
b. Quelle propriété le maître souhaite-t-il faire émerger en proposant cette situation ? Citer une difficulté qui peut faire obstacle à l'émergence de cette propriété ?
c. Pourquoi la consigne préalable aux questions 2, 3 et 4 précise-t-elle que la droite tracée ne doit pas être parallèle aux bords de la feuille ?
d. En prolongement de la question 4 du document 1, indiquer quel est l'ensemble constitué par tous les points situés à 7 cm de la droite ?
2) On considère maintenant le document 2 (copie d'écran).
Pour procéder à une synthèse de l'activité précédente, l'enseignant décide de projeter sur tableau blanc une figure réalisée avec un logiciel de géométrie dynamique. Le point P peut alors être déplacé sur la droite, et la distance AP s'afficher, comme sur la copie d'écran. Le point A et la droite peuvent également être déplacés.
Quel avantage peut apporter ce support, pour la connaissance visée, par rapport au dessin sur feuille des élèves ?
Exercice 3 (4 points)
1) On dispose de jetons bleus et de jetons rouges. Les jetons bleus ont pour valeur 3 points tandis que les jetons rouges ont pour valeur 7 points.
a. Pierre n'a que des jetons bleus et Jean n'a que des jetons rouges. Pierre doit donner 34 points à Jean. Comment Pierre et Jean peuvent-ils procéder ? Donner une solution.
b. Paul dit qu'il a 29 jetons qui représentent une valeur totale de 94 points. Que penser de l'affirmation de Paul ? Justifier la réponse.
c. Céline possède des jetons bleus et des jetons rouges pour une valeur totale de 34 points. Combien de jetons de chaque couleur possède-t-elle ? Trouver toutes les solutions.
2) Quel nombre maximum de rectangles de 3 cm de large et 7 cm de long peut-on effectivement obtenir en découpant une plaque rectangulaire de dimensions 21 cm et 34 cm ? Justifier la réponse.
On pourra utiliser le résultat de la question 1) c.
On pourra utiliser le résultat de la question 1) c.
Question complémentaire (3 points)
Observer les trois problèmes présentés dans l'annexe 2.
1) Dans quel cycle de l'école primaire ces problèmes pourraient-ils être traités ? Justifier la réponse.
2) Proposer deux erreurs différentes de procédure que pourraient commettre des élèves dans le problème n° 1.
3) Indiquer les principales étapes de la procédure que pourrait adopter un élève pour résoudre le problème n° 2.
4) Quelles connaissances supplémentaires par rapport aux deux problèmes précédents, la résolution du problème n° 3 suppose-t-elle ?
Annexes
Annexe 1
Document 1 Extrait d'un manuel de cycle 3 (Cap Maths, éd. Hatier, 2004.)
1) Place, sur la droite, le point qui est le plus proche du point A :
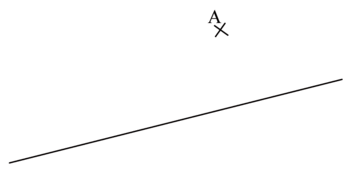 |
Pour les questions 2, 3 et 4, utilise à chaque fois une feuille de papier uni et trace une droite. La droite que tu traces ne doit pas être parallèle aux bords de la feuille.
2) Avec ton équipe, propose une méthode qui permet de placer, du premier coup, un point qui est exactement à 7 cm de la droite.
3) Place un point en dehors de la droite, nomme-le A.
Comment faire pour déterminer rapidement le point de la droite qui est le plus proche du point A ?
Comment faire pour déterminer rapidement le point de la droite qui est le plus proche du point A ?
4) Place rapidement et avec précision 24 points à 7 cm de la droite.
Document 2 Copie d'écran (logiciel de géométrie dynamique)
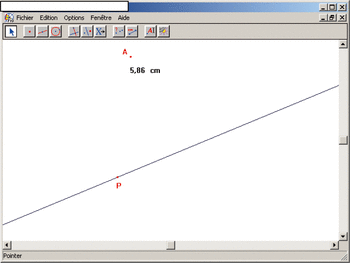 |
Annexe 2
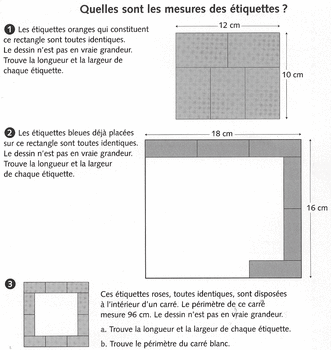
Extrait d'un manuel de la collection Cap maths éd. Hatier, 2004.
Les étiquettes mentionnées ci-dessous ne sont pas reproduites en couleur. Cela n'a aucune incidence dans le traitement des questions posées.
 |
Corrigé
Corrigé
Exercice 1 (4 points)
1) Les trois faces cachées du cube sont :
- HGCD qui est décorée avec des hachures ;
- EHDA qui est unie ;
- ADCB qui est décorée avec des points.
2) Les patrons n°1 et n°3 correspondent au cube ABCDHEFG.
Les patrons n°2 et n°4 ne correspondent pas au cube ABCDHEFG, les faces décorées avec les mêmes motifs étant adjacentes et non pas opposées.
Les patrons n°2 et n°4 ne correspondent pas au cube ABCDHEFG, les faces décorées avec les mêmes motifs étant adjacentes et non pas opposées.
3)
a. Si on considère les 3 « tranches » de 9 cubes chacune, on obtient 27 petits cubes contenus dans le grand.
b. Pour connaître le volume d'un petit cube, il suffit de diviser le volume du grand par le nombre de petits, soit : 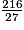 = 8.
= 8.
Chaque petit cube a un volume de 8 cm3.
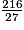 = 8.
= 8.Chaque petit cube a un volume de 8 cm3.
c. Puisqu'il s'agit de cubes, toutes les arêtes, a, sont isométriques. Le volume d'un petit cube est donc a3.
a3 = 8 d'où a = 2.
Chaque arête du petit cube mesure 2 cm.
Chaque arête du grand cube mesure 6 cm.
Vérification : le volume du grand cube est 63, soit 216 cm3.
On retrouve bien la valeur donnée dans l'énoncé.
a3 = 8 d'où a = 2.
Chaque arête du petit cube mesure 2 cm.
Chaque arête du grand cube mesure 6 cm.
Vérification : le volume du grand cube est 63, soit 216 cm3.
On retrouve bien la valeur donnée dans l'énoncé.
d.
| Nombre de faces décorées | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Nombre de petits cubes | 1 | 6 | 12 | 8 | 0 | 0 | 0 |
e. En utilisant le tableau précédent :
(6 × 1) + (12 × 2) + (8 × 3) = 54.
Il y a 54 petites faces décorées.
Cela correspond bien au nombre de faces de petits cubes sur les 6 faces du grand (9 × 6).
(6 × 1) + (12 × 2) + (8 × 3) = 54.
Il y a 54 petites faces décorées.
Cela correspond bien au nombre de faces de petits cubes sur les 6 faces du grand (9 × 6).
4)
a. Chaque petit cube a un volume de 8 cm3.
On retire 8 cubes de 8 cm3 au volume initial, soit 64 cm3.
216 − 64 = 152.
Le nouveau volume est de 152 cm3.
On retire 8 cubes de 8 cm3 au volume initial, soit 64 cm3.
216 − 64 = 152.
Le nouveau volume est de 152 cm3.
b. L'aire du cube amputé des petits cubes des sommets est la même que celle du cube entier, puisque les faces dégagées laissent apparaître d'autres faces, d'aire équivalente, qui étaient jusque-là cachées.
Par conséquent, l'aire du cube correspond à l'aire d'une face (36 cm2) multipliée par le nombre de faces.
36 × 6 = 216 cm2.
Par conséquent, l'aire du cube correspond à l'aire d'une face (36 cm2) multipliée par le nombre de faces.
36 × 6 = 216 cm2.
Exercice 2 (4 points)
1) Si on représente sur le schéma, 1 cm pour 1 km, cela veut dire que 1 cm sur le schéma représente 100 000 cm.
On dit que le schéma est à l'échelle 1/ 100 000.
On dit que le schéma est à l'échelle 1/ 100 000.
2)
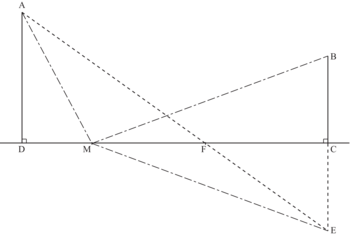 |
3) Soit E le symétrique de B par rapport à la droite (CD), et F l'intersection entre (AE) et (CD).
Les points A, F et E sont alignés. BF = FE.
Soit M, un point quelconque sur (CD) différent de F. Construisons le segment [ME].
On a alors ME = MB.
Comparons maintenant AM + MB et AF + FB.
AM + MB = AM + ME et AF + FB = AF + FE.
Les points A, F et E sont alignés, AE peut être considéré comme un côté du triangle AME et, d'après la définition de l'inégalité triangulaire, la longueur d'un côté d'un triangle est inférieure à la somme des longueurs des deux autres côtés. On a bien AE < AM + ME.
AF + FE < AM + ME
AF + FB < AM + MB ou AM + MB > AF + FB.
Les points A, F et E sont alignés. BF = FE.
Soit M, un point quelconque sur (CD) différent de F. Construisons le segment [ME].
On a alors ME = MB.
Comparons maintenant AM + MB et AF + FB.
AM + MB = AM + ME et AF + FB = AF + FE.
Les points A, F et E sont alignés, AE peut être considéré comme un côté du triangle AME et, d'après la définition de l'inégalité triangulaire, la longueur d'un côté d'un triangle est inférieure à la somme des longueurs des deux autres côtés. On a bien AE < AM + ME.
AF + FE < AM + ME
AF + FB < AM + MB ou AM + MB > AF + FB.
4) AF + FB étant la distance la plus courte pour relier A à B en passant par la droite (CD), c'est au point F que la gare sera construite.
G = F.
G = F.
5) Considérons les triangles AFD et ECF :
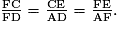
Sachant que CE = BC, on peut écrire :
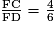 ;
;
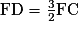 .
.
- AFD et ECF ont un sommet commun, F ;
- les points D, F et C sont alignés ;
- les points A, F et E sont alignés ;
- (AD) est parallèle à (EC).
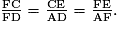
Sachant que CE = BC, on peut écrire :
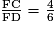 ;
;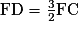 .
.6) FD = 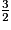 FC ;
FC ;
CD = 14 km ;
CD = FD + FC ;
14 =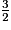 FC + FC ;
FC + FC ;
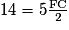 ;
;
5FC = 28 ;
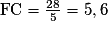 ;
;
FC = 5,6 km.
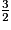 FC ;
FC ;CD = 14 km ;
CD = FD + FC ;
14 =
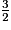 FC + FC ;
FC + FC ;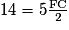 ;
;5FC = 28 ;
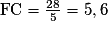 ;
;FC = 5,6 km.
7) Nous cherchons les mesures de FB et AF. Or, d'après le théorème de Pythagore, dans le triangle FCB, rectangle en C :
FB2 = FC2 + BC2 et AF2 = DF2 + AD2 ;
FB2 = (5,6)2 + 42 et AF2 = (14 − 5,6)2 + 62 ;
FB2 = 31,36 + 16 et AF2 = 70,56 + 36 ;
FB2 = 47,36 et AF2 = 106,56 ;
FB = 6,882 km et AF = 10,323 km ;
FB + AF = 6,882 + 10,323 ;
FB + AF = 17,205.
La longueur de la ville A à la ville B en passant par la gare G est 17,205 km.
FB2 = FC2 + BC2 et AF2 = DF2 + AD2 ;
FB2 = (5,6)2 + 42 et AF2 = (14 − 5,6)2 + 62 ;
FB2 = 31,36 + 16 et AF2 = 70,56 + 36 ;
FB2 = 47,36 et AF2 = 106,56 ;
FB = 6,882 km et AF = 10,323 km ;
FB + AF = 6,882 + 10,323 ;
FB + AF = 17,205.
La longueur de la ville A à la ville B en passant par la gare G est 17,205 km.
Question complémentaire (5 points)
1)
a. La première procédure pourrait être une démarche de tâtonnement, avec une règle graduée. Les élèves procéderaient en essayant plusieurs positions de la règle et en cherchant celle qui leur donne la plus petite distance entre le point et la droite en gardant chaque fois la mesure en tête.
La seconde peut consister à tracer plusieurs segments qui semblent adéquats, puis de les mesurer afin de déterminer lequel est le plus court.
Ils peuvent aussi travailler avec une bande de papier qu'ils déplacent et sur laquelle ils marquent les différentes mesures effectuées. Ils positionnent alors « définitivement« celle qui montre la mesure la plus courte.
[Si les élèves connaissent les propriétés de la mesure d'un point par rapport à une droite, ils utiliseront l'équerre et traceront le segment perpendiculaire à la droite passant par le point.
Ils peuvent aussi chercher le symétrique du point A par rapport à la droite, relieront les deux points, et trouveront leur distance par rapport à la droite. Il semblerait que cette démarche ne soit pas demandée, puisque cette solution experte devrait émerger des procédures personnelles des élèves, suivies à l'occasion des questions suivantes.]
La seconde peut consister à tracer plusieurs segments qui semblent adéquats, puis de les mesurer afin de déterminer lequel est le plus court.
Ils peuvent aussi travailler avec une bande de papier qu'ils déplacent et sur laquelle ils marquent les différentes mesures effectuées. Ils positionnent alors « définitivement« celle qui montre la mesure la plus courte.
[Si les élèves connaissent les propriétés de la mesure d'un point par rapport à une droite, ils utiliseront l'équerre et traceront le segment perpendiculaire à la droite passant par le point.
Ils peuvent aussi chercher le symétrique du point A par rapport à la droite, relieront les deux points, et trouveront leur distance par rapport à la droite. Il semblerait que cette démarche ne soit pas demandée, puisque cette solution experte devrait émerger des procédures personnelles des élèves, suivies à l'occasion des questions suivantes.]
b. Le maître souhaite faire émerger la propriété suivante : si A est un point extérieur à (d), H un point de (d) et [AH] perpendiculaire à (d) alors AH est la plus courte distance de A à un point de (d).
Les élèves peuvent ne pas repérer que le segment le plus court est perpendiculaire à la droite. Ils peuvent ne pas l'avoir tracé lors de la question 1, en ayant tracé d'autres segments. Ils peuvent n'avoir tracé aucun segment, puisque cela n'était pas demandé.
Ils peuvent aussi avoir des difficultés à construire une perpendiculaire qui passe par un point non situé sur la droite.
Les élèves peuvent ne pas repérer que le segment le plus court est perpendiculaire à la droite. Ils peuvent ne pas l'avoir tracé lors de la question 1, en ayant tracé d'autres segments. Ils peuvent n'avoir tracé aucun segment, puisque cela n'était pas demandé.
Ils peuvent aussi avoir des difficultés à construire une perpendiculaire qui passe par un point non situé sur la droite.
c. Il s'agit surtout de montrer que la règle existe quelle que soit l'orientation de la droite, les élèves ayant souvent tendance à assimiler verticale et perpendiculaire.
Toutefois, cette consigne n'a que peu d'influence sur les exercices, sauf, évidemment, pour le cas où la droite est parallèle ET à 7 cm du bord de la feuille. La recherche de la perpendiculaire est indépendante du parallélisme avec le bord de la feuille.
En revanche, il serait utile de préciser que la droite doit être tracée au milieu de la feuille afin que les 7 cm puissent être réellement mesurés.
Toutefois, cette consigne n'a que peu d'influence sur les exercices, sauf, évidemment, pour le cas où la droite est parallèle ET à 7 cm du bord de la feuille. La recherche de la perpendiculaire est indépendante du parallélisme avec le bord de la feuille.
En revanche, il serait utile de préciser que la droite doit être tracée au milieu de la feuille afin que les 7 cm puissent être réellement mesurés.
d. L'ensemble constitué par les 24 points situés à 7 cm de la droite est une autre droite qui lui est parallèle.
2) La première méthode employée par le maître était la construction par les élèves, d'une solution experte à partir de leurs solutions personnelles. Cette construction se faisait par groupes, les élèves étaient en activité de découverte par manipulation.
Dans le second cas, on est davantage dans une situation frontale d'enseignement, avec démonstration. C'est une autre entrée pédagogique, qui peut parfois sécuriser certains élèves, leur apporter les éléments qui leur manquaient pour progresser.
L'avantage de ce logiciel est de montrer de manière dynamique les relations qui existent entre la position du point P et la distance AP. On est dans la même situation que les élèves qui procédaient par essai au début, mais avec bien plus de latitude, puisque le logiciel offre la possibilité de retours en arrière.
Ensuite, le logiciel doit permettre de faire apparaître l'angle du segment [AP] et de la droite, ainsi que sa relation avec la distance entre A et P. Il s'agit de l'étape classique de mise en commun, non pas de productions figées, mais mais dynamiques, qui permettent de comprendre non seulement un résultat, mais une démarche.
Dans le second cas, on est davantage dans une situation frontale d'enseignement, avec démonstration. C'est une autre entrée pédagogique, qui peut parfois sécuriser certains élèves, leur apporter les éléments qui leur manquaient pour progresser.
L'avantage de ce logiciel est de montrer de manière dynamique les relations qui existent entre la position du point P et la distance AP. On est dans la même situation que les élèves qui procédaient par essai au début, mais avec bien plus de latitude, puisque le logiciel offre la possibilité de retours en arrière.
Ensuite, le logiciel doit permettre de faire apparaître l'angle du segment [AP] et de la droite, ainsi que sa relation avec la distance entre A et P. Il s'agit de l'étape classique de mise en commun, non pas de productions figées, mais mais dynamiques, qui permettent de comprendre non seulement un résultat, mais une démarche.
Exercice 3 (4 points)
1)
a. La question est peu précise et mérite d'être reformulée. En effet, Pierre ne peut pas « donner 34 points à Jean » avec ses seuls jetons bleus.
Il s'agit en fait de savoir comment faire pour que Jean ait 34 points avec les jetons rouges qu'il possède déjà et les jetons bleus que Pierre va lui donner.
On peut procéder en postulant que Jean a un maximum de jetons rouges, et que Pierre complète. Ainsi, Pour 34 points, Jean ne peut avoir plus de 4 jetons, (à partir de 5 jetons, il aurait 35 points).
Si Jean a 4 jetons rouges, il possède 28 points, il lui en manque donc 6 pour en avoir 34, soit 2 × 3.
Pierre lui donnera donc 2 jetons, soient 6 points (et pas « 34 » comme l'indique l'énoncé).
C'est une solution possible, il peut y en avoir d'autres.
Il s'agit en fait de savoir comment faire pour que Jean ait 34 points avec les jetons rouges qu'il possède déjà et les jetons bleus que Pierre va lui donner.
On peut procéder en postulant que Jean a un maximum de jetons rouges, et que Pierre complète. Ainsi, Pour 34 points, Jean ne peut avoir plus de 4 jetons, (à partir de 5 jetons, il aurait 35 points).
Si Jean a 4 jetons rouges, il possède 28 points, il lui en manque donc 6 pour en avoir 34, soit 2 × 3.
Pierre lui donnera donc 2 jetons, soient 6 points (et pas « 34 » comme l'indique l'énoncé).
C'est une solution possible, il peut y en avoir d'autres.
b. Posons les deux équations correspondant à cette affirmation.
Si x est le nombre de jetons rouges et y le nombre de jetons bleus :
x + y = 29 ;
7x + 3y = 94.
x = 29 − y ;
7 (29 − y) + 3y = 94 ;
203 − 7y + 3y = 94 ;
109 = 4y ;
y = 27, 25.
Ce résultat n'est pas un nombre entier. Il ne peut donc correspondre à un nombre de jetons.
Si x est le nombre de jetons rouges et y le nombre de jetons bleus :
x + y = 29 ;
7x + 3y = 94.
x = 29 − y ;
7 (29 − y) + 3y = 94 ;
203 − 7y + 3y = 94 ;
109 = 4y ;
y = 27, 25.
Ce résultat n'est pas un nombre entier. Il ne peut donc correspondre à un nombre de jetons.
c. Partant de la démarche de la question 1) a. nous déterminerons les solutions en débutant par le nombre maximum possible de jetons rouges.
Si Céline a 4 jetons rouges, (4 × 7 = 28), il lui manque 6 points, soient 2 jetons bleus.
Si Céline a 3 jetons rouges, (3 × 7 = 21) il lui manque 13 points, mais 13 n'est pas un multiple de 3.
Si Céline a 2 jetons rouges, (2 × 7 = 14) il lui manque 20 points, mais 20 n'est pas un multiple de 3.
Si Céline a 1 jeton rouge, (1 × 7 = 7) il lui manque 27 points, soient 9 jetons bleus (3 × 9).
Si Céline a 0 jeton rouge, (0 × 7 = 0) il lui manque 34 points, mais 34 n'est pas un multiple de 3.
Les deux solutions possibles sont donc :
Si Céline a 4 jetons rouges, (4 × 7 = 28), il lui manque 6 points, soient 2 jetons bleus.
Si Céline a 3 jetons rouges, (3 × 7 = 21) il lui manque 13 points, mais 13 n'est pas un multiple de 3.
Si Céline a 2 jetons rouges, (2 × 7 = 14) il lui manque 20 points, mais 20 n'est pas un multiple de 3.
Si Céline a 1 jeton rouge, (1 × 7 = 7) il lui manque 27 points, soient 9 jetons bleus (3 × 9).
Si Céline a 0 jeton rouge, (0 × 7 = 0) il lui manque 34 points, mais 34 n'est pas un multiple de 3.
Les deux solutions possibles sont donc :
- 4 jetons rouges et 2 jetons bleus ;
- et 1 jeton rouge et 9 jetons bleus.
2) On s'aidera de la question 1) c. Pour répondre à cette question, deux configurations sont possibles :
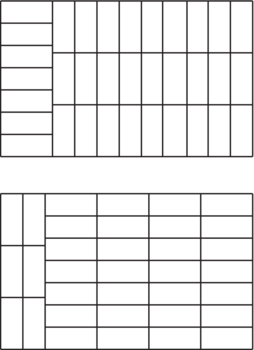 |
Dans les deux cas, nous aurons 34 rectangles, puisque l'aire du grand rectangle (A = 34 × 21) divisée par l'aire des petits (A1 = 3 × 7) est égale à 34.
34 × 21 = 714
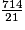 = 34 ;
= 34 ;
3 × 7 = 21.
34 × 21 = 714
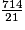 = 34 ;
= 34 ;3 × 7 = 21.
Question complémentaire (3 points)
1) Cette question trouve sa place au cycle 3 où, dans le domaine grandeurs et mesures, il est demandé « d'utiliser le calcul pour obtenir la mesure d'une grandeur et d'effectuer des calculs simples sur les mesures […] en particulier [dans le but de] calculer le périmètre d'un polygone ».
La combinaison de ces deux champs de compétences correspond aux exercices proposés.
La combinaison de ces deux champs de compétences correspond aux exercices proposés.
2) La donnée « 10 cm » n'est pas nécessaire pour résoudre le problème, puisque l'indication « 12 cm » suffit. Elle peut même constituer un piège, pour l'élève qui l'utilise à mauvais escient et déduit que la largeur du petit rectangle correspond à la moitié de la largeur du grand, soit 5 cm.
Il est possible aussi que, commettant une erreur d'appréciation, l'élève ne pense pas à diviser 12 par 3. Comptant 3 rectangles, il cherche alors un multiple de 3 et propose 3 cm comme largeur des petits rectangles.
Il est peu probable qu'une erreur soit commise sur les 6 cm, la figure faisant apparaître de façon claire le rapport entre la longueur du grand rectangle, mentionnée en haut et les longueurs des petits rectangles situés juste au-dessous.
Il est possible aussi que, commettant une erreur d'appréciation, l'élève ne pense pas à diviser 12 par 3. Comptant 3 rectangles, il cherche alors un multiple de 3 et propose 3 cm comme largeur des petits rectangles.
Il est peu probable qu'une erreur soit commise sur les 6 cm, la figure faisant apparaître de façon claire le rapport entre la longueur du grand rectangle, mentionnée en haut et les longueurs des petits rectangles situés juste au-dessous.
3) L'élève peut d'abord chercher la longueur de chaque étiquette, sachant que 3 longueurs correspondent à 18 cm. Il trouve donc 6 cm.
Ensuite, il calculera la mesure de deux longueurs d'étiquettes afin de les soustraire à la largeur du grand rectangle.
2 × 6 = 12 ;
16 − 12 = 4.
Il en déduira que deux largeurs d'étiquette mesurent 4 cm et qu'une largeur en mesure 2.
Ensuite, il calculera la mesure de deux longueurs d'étiquettes afin de les soustraire à la largeur du grand rectangle.
2 × 6 = 12 ;
16 − 12 = 4.
Il en déduira que deux largeurs d'étiquette mesurent 4 cm et qu'une largeur en mesure 2.
4) Dans la dernière question, l'élève doit connaître les propriétés du périmètre d'un carré, puisqu'on ne lui donne pas la valeur des longueurs des côtés.
Par ailleurs, le tour du carré étant complet, se fait jour une difficulté supplémentaire pour l'élève, qui doit déterminer « par où commencer », ce qui n'est pas le cas à l'exercice précédent, guidé.
La résolution de l'exercice 3 sera facilité pour l'élève, si celui-ci a d'abord effectué l'exercice n°2, qui lui permet d'avoir une méthode à appliquer.
Par ailleurs, le tour du carré étant complet, se fait jour une difficulté supplémentaire pour l'élève, qui doit déterminer « par où commencer », ce qui n'est pas le cas à l'exercice précédent, guidé.
La résolution de l'exercice 3 sera facilité pour l'élève, si celui-ci a d'abord effectué l'exercice n°2, qui lui permet d'avoir une méthode à appliquer.
