Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (3 points)
Pour la fête de l'école, des parents d'élèves ont confectionné des flans pâtissiers et des tartes aux pommes.
1)
Une part de flan pâtissier est vendue 1,50 € et une part de tarte aux pommes 2,00 €. Dans l'après-midi, 72 parts de gâteaux ont été vendues pour une recette totale de 122,00 €.
Déterminer le nombre de parts de chaque sorte qui ont été vendues :
Déterminer le nombre de parts de chaque sorte qui ont été vendues :
a. par une méthode algébrique ;
b. par un raisonnement de type arithmétique.
2) À la fin de l'après-midi, il reste une tarte aux pommes entière. Quatre enfants se partagent ce gâteau de la façon suivante : Jean-Marc se sert en premier et en prend un tiers ; Sophie prend trois huitièmes de ce qu'a laissé Jean-Marc ; enfin, Antoine et Rémi se partagent le reste de façon équitable.
À quelle fraction de tarte correspond la portion de chaque enfant ?
À quelle fraction de tarte correspond la portion de chaque enfant ?
Question complémentaire (4 points)
L'annexe 1 présente l'énoncé d'un problème ainsi que les productions écrites de quatre élèves A, B, C et D.
1) Dans quel cycle de l'école primaire cette situation peut-elle être proposée ? Justifier la réponse.
2) Pour chaque élève, décrire la procédure utilisée et analyser les erreurs éventuelles en formulant des hypothèses sur leurs origines.
3) En référence aux documents d'application des programmes dont un extrait est reproduit en annexe 2, indiquer à quel type d'écrits correspondent les productions des quatre élèves. Justifier la réponse.
Exercice 2 (5 points)
Un horticulteur envisage la construction d'une serre ayant la forme d'un parallélépipède rectangle surmonté d'une pyramide comme l'indique la figure ci-après.
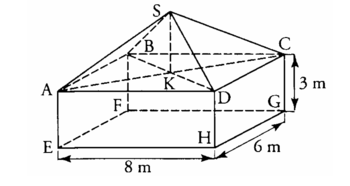 |
On désigne par x la mesure de la hauteur SK (exprimée en mètres) de la pyramide SABCD.
1) Montrer que la mesure V du volume (en m3) de la serre est donnée par la formule V = 144 + 16x.
2) Calculer ce volume pour x = 1,5.
3) Pour quelle valeur de x la serre a-t-elle un volume de 200 m3 ?
On s'intéresse maintenant à la surface vitrée de la serre (surface constituée des quatre faces latérales et du toit).
Le graphique ci-après donne l'aire de la surface vitrée en fonction de la hauteur x de la pyramide.
Le graphique ci-après donne l'aire de la surface vitrée en fonction de la hauteur x de la pyramide.
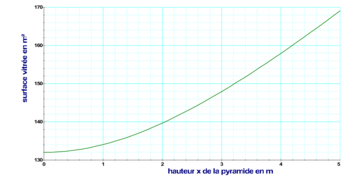 |
4) Par lecture graphique, donner l'aire de la surface vitrée correspondant à x = 4,20.
5) Pour des raisons de coût, l'horticulteur souhaite limiter l'aire de la surface vitrée à 150 m2. Quelle est, dans ce cas, la hauteur maximum de la pyramide indiquée par le graphique ?
6) Dans le cas où x = 0, préciser la forme de la serre. Quelle aire de la surface vitrée le graphique indique-t-il ? Retrouver ce résultat par le calcul.
Pour toutes les questions suivantes, on prendra SK = 3 m (c'est-à-dire x = 3).
7) Calculer la hauteur issue de S du triangle SDC.
8)
a. En utilisant le quadrillage de la feuille de copie, reproduire le triangle SDC à l'échelle 1/200.
b. En utilisant le côté [SD] de la figure précédente, construire à la règle et au compas une reproduction à l'échelle 1/200 du triangle SAD. Laisser apparents les traits de construction.
Exercice 3 (4 points)
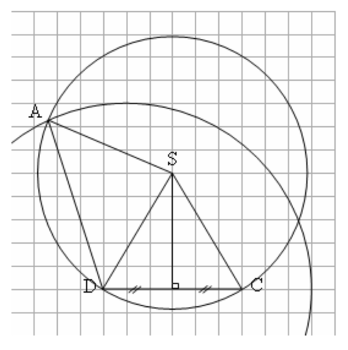
ABC est un triangle isocèle rectangle en B. Le côté [AC] mesure 15 cm.
I désigne le milieu du segment [BC] et J celui du segment [BA].
I désigne le milieu du segment [BC] et J celui du segment [BA].
1) Tracer, en utilisant le quadrillage de la feuille de copie, le segment [AC] puis construire à la règle et au compas le triangle ABC ainsi que les points I et J. Laisser apparents les traits de construction.
2)
a. Calculer l'aire du triangle ABC.
b. En déduire l'aire du triangle AIC. Justifier la réponse.
3)
On appelle D l'intersection des droites (AI) et (CJ). On nomme K le milieu du segment [AC].
a. Montrer que les points B, D et K sont alignés.
b. Calculer la longueur du segment [DK].
c. Calculer l'aire du triangle ADC.
d. Calculer l'aire du quadrilatère ABCD.
Question complémentaire (4 points)
Cette question s'appuie sur le document proposé en annexe 3, extrait du manuel Euromaths CM2 (Hatier). Il s'agit d'un extrait de la leçon 55, en fin de période 3. Les fractions et les nombres décimaux ont été travaillés en période 1.
1)
On s'intéresse à la question 1 du document.
a. Indiquer et décrire deux procédures que peut utiliser un élève pour répondre correctement à la question 1.
b. Un élève ne voit pas que les figures C, D et F ont la même aire. Indiquer une raison possible de cette difficulté. Quelle aide peut lui être apportée ?
c. Après cette activité, que peut faire noter le maître dans le cahier de leçon concernant deux surfaces de même aire ?
2)
On s'intéresse à la question 3 du document.
a. Décrire la procédure qu'un élève peut utiliser pour répondre à la question.
b. Choisir une autre unité d'aire afin que les réponses des élèves à cette question ne fassent appel qu'à des nombres entiers. Justifier la réponse.
Annexe 1
Arnaud est allé voir les poules et les lapins de son voisin. En revenant, il pose à son frère la devinette suivante : « J'ai compté les têtes de tous les animaux et j'ai trouvé 4. J'ai ensuite compté les pattes et j'ai trouvé 14. Peux-tu me dire combien il y a d'animaux de chaque sorte ? »
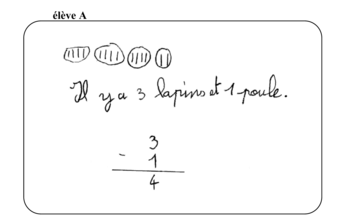 |
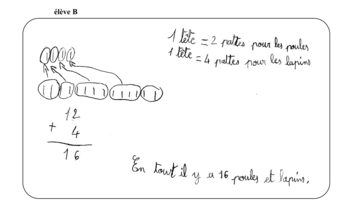 |
 |
 |
Annexe 2
Écrire en mathématiques« Les élèves sont fréquemment placés en situation de production d'écrits. Il convient à cet égard de développer et de bien distinguer trois types d'écrits dont les fonctions sont différentes :
- les écrits de type « recherche » correspondent au travail privé de l'élève. Ils ne sont pas destinés à être communiqués, ils peuvent comporter des dessins, des schémas, des figures, des calculs. Ils sont un support pour essayer, se rendre compte d'une erreur, reprendre, rectifier, organiser sa recherche. Ils peuvent également être utilisés comme mémoire transitoire au cours de la résolution du problème. Si l'enseignant est amené à les consulter pour étudier le cheminement de l'élève, il ne doit ni les critiquer, ni les corriger ;
- les écrits destinés à être communiqués et discutés peuvent prendre des formes diverses (par exemple, affiche, transparent). Ils doivent faire l'objet d'un souci de présentation, de lisibilité, d'explicitation, tout en sachant que, le plus souvent, ils seront l'objet d'un échange entre les élèves au cours duquel des explications complémentaires seront apportées ;
- les écrits de référence sont élaborés en vue de constituer une mémoire du travail de l'élève ou de la classe. Ils sont donc destinés à être conservés et doivent être rédigés dans une forme correcte.
Ministère de l'Éducation nationale, Document d'application des programmes, extrait, éd. CNDP, juillet 2002
Annexe 3
 |
Corrigé
Corrigé
Exercice 1 (3 points)
1)
a. Soit x le nombre de parts de flan et soit y le nombre de parts de tarte.
On résout le système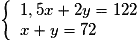 .
.
On multiplie par 2 les membres de la 2e équation : 2x + 2y = 144.
On soustrait les membres de cette équation à la 1re équation :
2x + 2y − 1,5x − 2y = 144 − 122
0,5x = 22
x = 44.
On remplace la valeur de x dans la 1re équation pour trouver y :
1,5 × 44 + 2y = 122
2y = 122 − 66
y = 28.
Donc il a été vendu 44 parts de flan et 28 parts de tarte aux pommes.
On résout le système
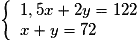 .
.On multiplie par 2 les membres de la 2e équation : 2x + 2y = 144.
On soustrait les membres de cette équation à la 1re équation :
2x + 2y − 1,5x − 2y = 144 − 122
0,5x = 22
x = 44.
On remplace la valeur de x dans la 1re équation pour trouver y :
1,5 × 44 + 2y = 122
2y = 122 − 66
y = 28.
Donc il a été vendu 44 parts de flan et 28 parts de tarte aux pommes.
b. Sur 72 parts vendues, supposons que la moitié des parts, c'est-à-dire 36 parts, soient des parts de flan et 36 soient des parts de tarte aux pommes. Calculons alors la recette : 36 × 1,5 + 36 × 2 = 126.
Or la recette est de 122 €, donc il a été vendu plus de 36 parts de flan, étant donné que ce sont les parts les moins chères.
Calculons la recette pour 38 parts de flan : 36 × 1,5 + 34 × 2 = 125.
Par tâtonnements successifs, on trouve 44 parts de flan et 28 parts de tarte aux pommes.
Or la recette est de 122 €, donc il a été vendu plus de 36 parts de flan, étant donné que ce sont les parts les moins chères.
Calculons la recette pour 38 parts de flan : 36 × 1,5 + 34 × 2 = 125.
Par tâtonnements successifs, on trouve 44 parts de flan et 28 parts de tarte aux pommes.
2) Jean-Marc en prend 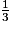 , donc il reste les
, donc il reste les 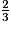 de la tarte.
de la tarte.
Sophie prend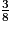 de
de 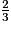 . On calcule
. On calcule 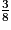 ×
× 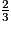 =
= 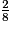 =
= 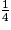 .
.
Elle a donc pris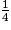 de la tarte.
de la tarte.
Calculons ce qu'ont pris Jean-Marc et Sophie :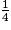 +
+ 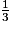 =
= 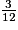 +
+ 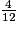 =
= 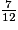 .
.
Il reste après eux : 1 −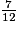 =
= 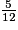 .
.
Antoine et Rémi ont donc pris chacun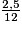 , soit
, soit 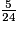 de la tarte.
de la tarte.
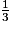 , donc il reste les
, donc il reste les 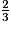 de la tarte.
de la tarte.Sophie prend
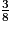 de
de 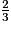 . On calcule
. On calcule 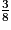 ×
× 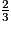 =
= 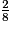 =
= 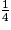 .
.Elle a donc pris
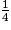 de la tarte.
de la tarte.Calculons ce qu'ont pris Jean-Marc et Sophie :
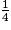 +
+ 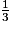 =
= 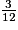 +
+ 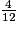 =
= 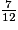 .
.Il reste après eux : 1 −
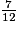 =
= 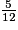 .
.Antoine et Rémi ont donc pris chacun
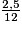 , soit
, soit 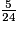 de la tarte.
de la tarte.Question complémentaire (4 points)
1) Cette situation peut être proposée en début de cycle 3 car elle nécessite un dénombrement différencié sans support. En effet, c'est aux élèves eux-mêmes de se représenter cette situation, et l'objectif à atteindre est double : avoir 4 animaux et 14 pattes.
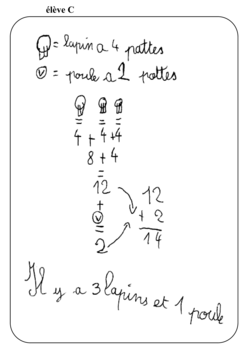
2) L'élève A dessine des bâtons qui représentent les pattes et regarde combien de paquets de 4 il peut faire dans 14 pour trouver le nombre de lapins. Il fait 3 paquets de 4 bâtons et complète avec un paquet de 2. Il trouve la bonne réponse : 3 lapins et 1 poule. Seule l'opération qu'il pose, 3 − 1, n'a pas de sens.
L'élève B commence par faire 2 paquets de 2 pattes (c'est-à-dire 2 poules), puis se rend compte que le nombre de pattes est très insuffisant pour arriver à 14, donc il ajoute 2 paquets de 4 pattes (afin de représenter 2 lapins), et il rajoute enfin 1 paquet de 2 pattes pour arriver à 14.
Ensuite, avec un système de flèches, il ne sélectionne que les 4 premiers paquets pour avoir 4 et non 5 animaux au total. Il n'arrive pas à voir qu'il doit enlever une poule et la remplacer par un lapin. Enfin, il pose une addition d'un nombre de pattes et d'un nombre d'animaux, ce qui est faux.
L'élève C a un raisonnement analogue à l'élève A, il écrit toutes ses recherches et trouve la bonne réponse.
L'élève D dessine 4 têtes de lapins pour avoir les 4 animaux demandés, puis il dessine 7 paquets de 2 bâtons qui représentent pour lui les 14 pattes de 7 poules. Il n'arrive pas à travailler sur les deux objectifs (4 animaux et 14 pattes) en même temps.
L'élève B commence par faire 2 paquets de 2 pattes (c'est-à-dire 2 poules), puis se rend compte que le nombre de pattes est très insuffisant pour arriver à 14, donc il ajoute 2 paquets de 4 pattes (afin de représenter 2 lapins), et il rajoute enfin 1 paquet de 2 pattes pour arriver à 14.
Ensuite, avec un système de flèches, il ne sélectionne que les 4 premiers paquets pour avoir 4 et non 5 animaux au total. Il n'arrive pas à voir qu'il doit enlever une poule et la remplacer par un lapin. Enfin, il pose une addition d'un nombre de pattes et d'un nombre d'animaux, ce qui est faux.
L'élève C a un raisonnement analogue à l'élève A, il écrit toutes ses recherches et trouve la bonne réponse.
L'élève D dessine 4 têtes de lapins pour avoir les 4 animaux demandés, puis il dessine 7 paquets de 2 bâtons qui représentent pour lui les 14 pattes de 7 poules. Il n'arrive pas à travailler sur les deux objectifs (4 animaux et 14 pattes) en même temps.
3) L'écrit de l'élève A est uniquement de type recherche. Ce qu'il dessine et écrit est très court. On peut donc imaginer que cet élève comprend vite et bien. Sa production n'est pas du tout destinée à être communiquée à d'autres élèves.
Par contre, les écrits des élèves B et C sont des traces de recherche qui ont aussi pour but d'être communiquées. En effet, tous les deux utilisent un système de légende pour se faire comprendre des autres et écrivent des calculs plus ou moins détaillés.
La production de l'élève D ne montre aucune recherche, aucun calcul. Cet élève s'est appliqué à faire de beaux dessins de têtes de lapins, ce qui sans doute parasite son raisonnement : son écrit a pour but d'être beau et d'être communiqué.
Par contre, les écrits des élèves B et C sont des traces de recherche qui ont aussi pour but d'être communiquées. En effet, tous les deux utilisent un système de légende pour se faire comprendre des autres et écrivent des calculs plus ou moins détaillés.
La production de l'élève D ne montre aucune recherche, aucun calcul. Cet élève s'est appliqué à faire de beaux dessins de têtes de lapins, ce qui sans doute parasite son raisonnement : son écrit a pour but d'être beau et d'être communiqué.
Exercice 2 (5 points)
1) V = V pavé + V pyramide
V = 8 × 6 × 3 + 8 × 6 ×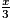
V = 144 + 16x.
V = 8 × 6 × 3 + 8 × 6 ×
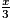
V = 144 + 16x.
2) Pour x = 1,5, V = 144 + 16 × 1,5 = 168 m3.
3) On résout l'équation 144 + 16x = 200
16x = 200 − 144
16x = 56
x = 3,5.
16x = 200 − 144
16x = 56
x = 3,5.
4) Pour x = 4,2, l'aire de la surface vitrée est égale à 160 m2.
5) Pour limiter l'aire de la surface vitrée à 150 m2, la hauteur maximum de la pyramide est 3,2 m.
6) Pour x = 0, la serre a la forme d'un pavé droit, et graphiquement on lit que l'aire de la surface vitrée est 132 m2.
Par le calcul : Aire totale des 5 faces du pavé = (8 × 3) × 2 + (6 × 3) × 2 + 8 × 6 = 132 m2.
Par le calcul : Aire totale des 5 faces du pavé = (8 × 3) × 2 + (6 × 3) × 2 + 8 × 6 = 132 m2.
7) On applique le théorème de Pythagore dans le triangle ABC pour trouver d'abord AC :
AC2 = AB2 + BC2
AC2 = 82 + 62
AC2 = 100, donc AC =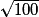 = 10 m.
= 10 m.
ABCD est un rectangle, donc ses diagonales se coupent en leur milieu, donc KD =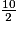 = 5 m.
= 5 m.
On calcul SD dans le triangle SKD en appliquant le théorème de Pythagore :
SD2 = 32 + 52
SD2 = 34, donc SD =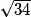 m.
m.
SDC est un triangle isocèle en S : hauteur de SDC =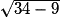 = 5 m.
= 5 m.
AC2 = AB2 + BC2
AC2 = 82 + 62
AC2 = 100, donc AC =
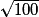 = 10 m.
= 10 m.ABCD est un rectangle, donc ses diagonales se coupent en leur milieu, donc KD =
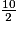 = 5 m.
= 5 m.On calcul SD dans le triangle SKD en appliquant le théorème de Pythagore :
SD2 = 32 + 52
SD2 = 34, donc SD =
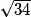 m.
m.SDC est un triangle isocèle en S : hauteur de SDC =
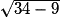 = 5 m.
= 5 m.8)
a. L'échelle 1/200 signifie que 1 cm sur le dessin représente 200 cm en réalité, soit 2 m.
DC = 6 m = 600 cm et hauteur issue de S dans SDC = 5 m = 500 cm.
On construit donc le triangle SDC avec DC = 3 cm et on trace la hauteur issue de S égale à 2,5 cm.
| Dimensions en réalité (en cm) | 600 | 500 |
| Dimensions sur le dessin (en cm) | 3 | 2,5 |
DC = 6 m = 600 cm et hauteur issue de S dans SDC = 5 m = 500 cm.
On construit donc le triangle SDC avec DC = 3 cm et on trace la hauteur issue de S égale à 2,5 cm.
 |
b. À l'échelle 1/200, AD est égale à 4 cm sur le dessin.
 |
Exercice 3 (4 points)
1)
 |
2)
a. On calcule AB en appliquant le théorème de Pythagore dans le triangle ABC : AC2 = AB2 + BC2.
Or ABC est isocèle en B, donc BC = AB.
Donc AC2 = 2 x AB2
152 = 2AB2
AB2 =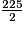 , d'où AB =
, d'où AB = 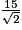 cm.
cm.
Aire de ABC =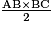 =
= 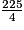 cm2, soit 56,25 cm2.
cm2, soit 56,25 cm2.
Or ABC est isocèle en B, donc BC = AB.
Donc AC2 = 2 x AB2
152 = 2AB2
AB2 =
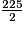 , d'où AB =
, d'où AB = 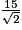 cm.
cm.Aire de ABC =
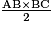 =
= 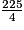 cm2, soit 56,25 cm2.
cm2, soit 56,25 cm2.b. Aire de AIC = Aire de ABC − Aire de AIB.
On calcule l'aire du triangle AIB :
Aire de AIB =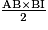 = (
= (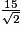 ×
× 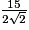 ) / 2 =
) / 2 = 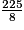 cm2, soit 28,125 cm2.
cm2, soit 28,125 cm2.
Donc Aire de AIC = 56,25 − 28,125 = 28,125 cm2.
On calcule l'aire du triangle AIB :
Aire de AIB =
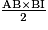 = (
= (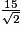 ×
× 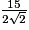 ) / 2 =
) / 2 = 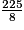 cm2, soit 28,125 cm2.
cm2, soit 28,125 cm2.Donc Aire de AIC = 56,25 − 28,125 = 28,125 cm2.
3)
a. D est le centre de gravité du triangle ABC, le point d'intersection des médianes (AI) et (BJ) ; K est le milieu de [AC], donc la droite (BK) est la 3e médiane du triangle ABC.
Donc D, B et K sont alignés.
Donc D, B et K sont alignés.
b. ABC est isocèle en B, donc la médiane et la hauteur issue de B sont confondues.
Aire de ABC =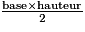
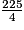 =
= 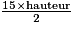
donc hauteur = BK =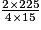 = 7,5 cm.
= 7,5 cm.
D étant le centre de gravité du triangle ABC, on a : DK =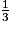 BK =
BK = 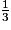 × 7,5 = 2,5 cm.
× 7,5 = 2,5 cm.
Aire de ABC =
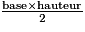
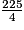 =
= 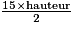
donc hauteur = BK =
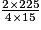 = 7,5 cm.
= 7,5 cm.D étant le centre de gravité du triangle ABC, on a : DK =
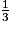 BK =
BK = 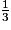 × 7,5 = 2,5 cm.
× 7,5 = 2,5 cm.c. Aire de ADC = 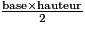 =
= 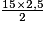 = 18,75 cm2.
= 18,75 cm2.
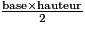 =
= 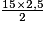 = 18,75 cm2.
= 18,75 cm2.d. Aire de ABCD = Aire de ABC − Aire de ADC = 56,25 − 18,75 = 37,5 cm2.
Question complémentaire (4 points)
1)
a. En positionnant la pièce A sur la pièce B, l'élève se rend compte que les pièces A et B ont la même aire. De la même façon, il trouve que les pièces E et G ont la même aire.
Il peut découper la pièce D en deux parties égales et constater que les pièces E, F et la moitié de la pièce D permettent de former en puzzle la pièce A. De même, les pièces G, C et la moitié de la pièce D permettent de former en puzzle la pièce A.
On a Aire A = Aire E + Aire F + Aire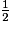 D = Aire G + Aire C + Aire
D = Aire G + Aire C + Aire 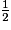 D.
D.
On en déduit, comme Aire E = Aire G, que Aire F = Aire C.
Par ailleurs, les deux triangles isométriques obtenus de la découpe de D permettent par recollement différent d'obtenir F et donc de voir que Aire D = Aire F.
Il peut découper la pièce D en deux parties égales et constater que les pièces E, F et la moitié de la pièce D permettent de former en puzzle la pièce A. De même, les pièces G, C et la moitié de la pièce D permettent de former en puzzle la pièce A.
On a Aire A = Aire E + Aire F + Aire
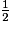 D = Aire G + Aire C + Aire
D = Aire G + Aire C + Aire 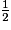 D.
D.On en déduit, comme Aire E = Aire G, que Aire F = Aire C.
Par ailleurs, les deux triangles isométriques obtenus de la découpe de D permettent par recollement différent d'obtenir F et donc de voir que Aire D = Aire F.
b. C, F et D n'ont pas la même forme, donc l'élève ne voit pas immédiatement que ces pièces ont la même aire. L'aide à apporter consiste à tracer dans D et dans C deux triangles identiques : on constate que les deux triangles ainsi obtenus permettent après découpage de reconstituer le carré F.
c. Après cette activité, le maître pourra faire noter dans le cahier de leçon que deux figures différentes peuvent avoir la même aire.
2)
a. L'aire du carré est 8 × 8 = 64 cm2.
Donc les pièces A et B ont une aire de 32 cm2, F, D et C de 16 cm2, E et G de 8 cm2.
L'élève va utiliser les pièces du puzzle pour trouver les figures proposées :
T aura donc une aire de 24 cm2, V de 40 cm2 et W de 64 cm2.
Donc les pièces A et B ont une aire de 32 cm2, F, D et C de 16 cm2, E et G de 8 cm2.
L'élève va utiliser les pièces du puzzle pour trouver les figures proposées :
- pour T, il va juxtaposer les pièces F et E ;
- pour V, il va juxtaposer les pièces D, C et E ;
- pour W, il va juxtaposer les pièces C, A et F.
T aura donc une aire de 24 cm2, V de 40 cm2 et W de 64 cm2.
b. On peut choisir comme unité d'aire celle de la pièce E.
On aura alors :
On aura alors :
- aire de T = 3 × aire de E = 3u ;
- aire de V = 5 × aire de E = 5u ;
- aire de W = 8 × aire de E = 8u.
