Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (5 points)
ABCD est un rectangle tel que AB = 6,5 et AD = 4, l'unité de mesure étant le centimètre.
M, N, P et Q sont des points respectivement sur les segments [AB], [BC], [CD] et [AD], et tels que AM = BN = CP = DQ.
On s'intéresse dans cet exercice à la variation de l'aire du quadrilatère MNPQ en fonction de la position du point M.
M, N, P et Q sont des points respectivement sur les segments [AB], [BC], [CD] et [AD], et tels que AM = BN = CP = DQ.
On s'intéresse dans cet exercice à la variation de l'aire du quadrilatère MNPQ en fonction de la position du point M.
Toute réponse devra être justifiée.
On pose AM = x.
1. Construire la figure dans le cas x = 4. Démontrer que MNPQ est un parallélogramme. Calculer son aire.
2. Choisir une valeur de x dans l'intervalle ]0, 4[ et construire la figure correspondante. Quelle est la nature du quadrilatère MNPQ ?
3. a) On suppose que 0 < x < 4. Exprimer l'aire de MNPQ en fonction de x.
b) La formule obtenue en a) fournit-elle le bon résultat si on l'applique à x = 0 ? à x = 4 ?
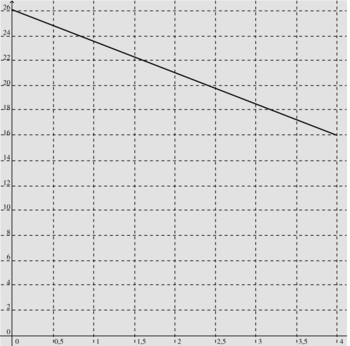
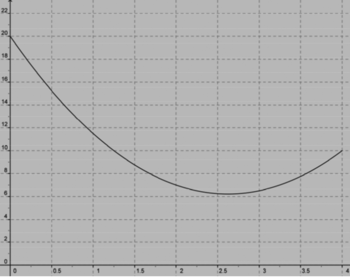
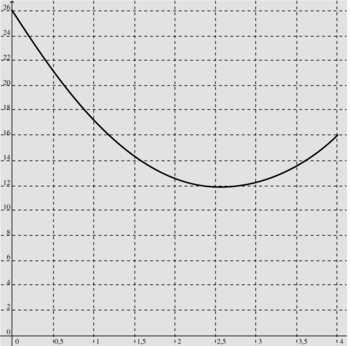
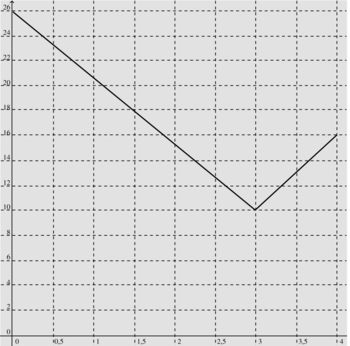
4. L'une des quatre courbes ci-dessous représente la variation de l'aire de MNPQ en fonction de x. Laquelle ?
 |
 |
 |
 |
5. Déterminer par lecture graphique sur cette courbe :
a) Au demi-centimètre près, la valeur de x pour laquelle l'aire de MNPQ est minimale.
b) Au centimètre carré près, la valeur de l'aire minimale.
6. Dans cette question on utilise un tableur pour étudier l'aire du quadrilatère MNPQ en fonction de x. Différentes valeurs de x sont inscrites sur la ligne 1.
 |
a) Donner une formule qui, entrée dans la cellule B2, puis recopiée vers la droite, a pu permettre de compléter la ligne 2.
b) Expliquer pourquoi on ne peut pas conclure de façon certaine que 12,22 cm2 est une valeur approchée de l'aire minimale à 0,1 cm2 près.
7. Montrer que l'on peut exprimer l'aire de MNPQ trouvée à la question 3. sous la forme :
Aire(MNPQ) =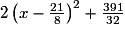
En déduire la valeur de l'aire minimale de MNPQ et la valeur de x à laquelle elle correspond.
Aire(MNPQ) =
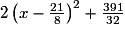
En déduire la valeur de l'aire minimale de MNPQ et la valeur de x à laquelle elle correspond.
Exercice 2 (4 points)
Dans cet exercice, sept affirmations sont proposées. Pour chacune d'elles, dire si elle est vraie ou fausse et justifier la réponse.
Une réponse exacte mais non justifiée ne rapporte aucun point.
Une réponse fausse n'enlève pas de point.
Une réponse exacte mais non justifiée ne rapporte aucun point.
Une réponse fausse n'enlève pas de point.
1. Depuis 5 ans, les prix augmentent de 10 % par an.
Affirmation 1 : « En 5 ans, les prix ont augmenté de 50 %. »
Affirmation 1 : « En 5 ans, les prix ont augmenté de 50 %. »
2. Affirmation 2 : « En versant 5 volumes de sirop de fraise dans 9 volumes d'eau, on aura une boisson plus sucrée que si l'on verse 4 volumes du même sirop dans 7 volumes d'eau. »
3. On utilise une roulette (de type casino) avec 5 cases numérotées 1 ; 2 ; 3 ; 4 ; 5. Cette roulette est truquée. Le tableau ci-dessous précise la probabilité d'obtenir chacun des numéros (où p est un nombre positif).
Affirmation 3 : « On a autant de chances d'obtenir un nombre pair qu'un nombre impair. »
| Nombre obtenu | 1 | 2 | 3 | 4 | 5 |
| Probabilité | 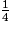 | p | p | 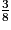 | p |
Affirmation 3 : « On a autant de chances d'obtenir un nombre pair qu'un nombre impair. »
4. Affirmation 4 : « La différence entre les carrés de deux nombres entiers naturels consécutifs est égale à la somme de ces deux nombres entiers. »
5. Affirmation 5 : « Si on augmente l'arête d'un cube de 10 %, alors le volume de ce cube augmente de 33,1 %. »
6. En position dite de « l'œuf », un skieur augmente de 50 % sa vitesse moyenne et descend ainsi la piste à 120 km/h.
Affirmation 6 : « Sans cette technique, sa vitesse moyenne n'est donc que de 60 km/h. »
Affirmation 6 : « Sans cette technique, sa vitesse moyenne n'est donc que de 60 km/h. »
7. Sur la figure ci-dessous, C est un point du demi-cercle de diamètre [AB].
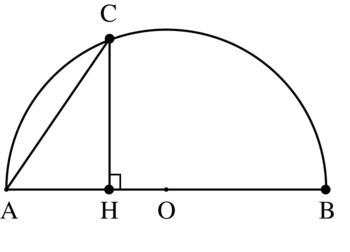 |
Affirmation 7 : « Si AB = n et AH = 1, alors AC = 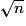 . »
. »
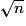 . »
. »Exercice 3 (3 points)
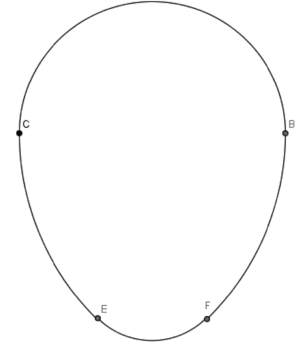
L'ove est une figure géométrique, constituée de quatre arcs de cercle, dont la forme fait penser à un œuf.
On a représenté ci-dessous un ove BCEF (la figure n'est pas en vraie grandeur).
Pour cet ove on sait que :
On a représenté ci-dessous un ove BCEF (la figure n'est pas en vraie grandeur).
Pour cet ove on sait que :
- la partie supérieure de l'ove est un demi-cercle de diamètre [BC] avec BC = 10 cm et le reste de la figure est dans le demi-plan de frontière (BC) ne contenant pas ce demi-cercle ;
- D est le point de ce demi-plan tel que le triangle BCD soit isocèle et rectangle en D ;
- l'arc de cercle
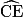 a pour centre B avec BDE alignés ;
a pour centre B avec BDE alignés ; - l'arc de cercle
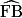 a pour centre C avec CDF alignés ;
a pour centre C avec CDF alignés ; - l'arc de cercle
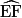 a pour centre D.
a pour centre D.
 |
1. Construire en vraie grandeur l'ove ainsi défini.
2. Calculer le périmètre de l'ove construit à la question précédente (on donnera le résultat arrondi au millimètre).
Corrigé
Corrigé
Exercice 1
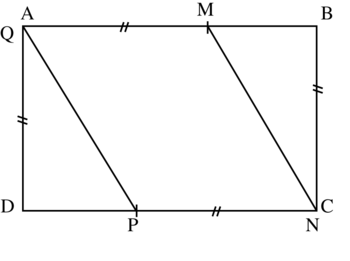
1. Construction de la figure lorsque x = 4.
 |
Montrons que MNPQ est un parallélogramme.
Lorsque x = 4, A et Q sont confondus, tout comme N et C. Il s'agit donc de montrer que MCPA est un parallélogramme.
Nous savons que M est sur le segment [AB] et que P est sur le segment [CD] ; or, ABCD étant un rectangle, ces segments sont parallèles. On en déduit que les segments [AM] et [CP] sont parallèles. Comme par ailleurs AM = CP, les côtés [AM] et [CP] du quadrilatère AMCP sont parallèles et de même longueur.
Un quadrilatère dont deux côtés sont de même longueur et parallèles est un parallélogramme, donc AMCP (autrement dit ici : MNPQ) est un parallélogramme.
Lorsque x = 4, A et Q sont confondus, tout comme N et C. Il s'agit donc de montrer que MCPA est un parallélogramme.
Nous savons que M est sur le segment [AB] et que P est sur le segment [CD] ; or, ABCD étant un rectangle, ces segments sont parallèles. On en déduit que les segments [AM] et [CP] sont parallèles. Comme par ailleurs AM = CP, les côtés [AM] et [CP] du quadrilatère AMCP sont parallèles et de même longueur.
Un quadrilatère dont deux côtés sont de même longueur et parallèles est un parallélogramme, donc AMCP (autrement dit ici : MNPQ) est un parallélogramme.
Calcul de l'aire de MNPQ.
AMNPQ = base × hauteur = MQ × AD = AM × AD = 4 × 4 = 16 cm2.
AMNPQ = base × hauteur = MQ × AD = AM × AD = 4 × 4 = 16 cm2.
2. Construction de la figure pour une valeur quelconque de x de l'intervalle ]0 ; 4[.
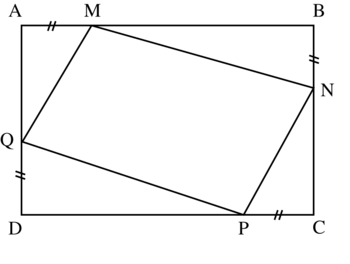 |
Nature du quadrilatère MNPQ.
Je sais que : AM = PC, que AB = CD (car ABCD est un rectangle) et que : M [AB] et P
[AB] et P [CD] ; j'en déduis que : BM = PD.
[CD] ; j'en déduis que : BM = PD.
De même, je sais que : BN = DQ, que BC = DA (car ABCD est un rectangle) et que : N [BC] et Q
[BC] et Q [DA] ; j'en déduis que : NC = AQ.
[DA] ; j'en déduis que : NC = AQ.
Les triangles AMQ et CPN sont rectangles et tels que : AM = CP et AQ = CN. Ces triangles sont donc isométriques (superposables) ; j'en déduis que : MQ = NP.
De même, les triangles BMN et DPQ sont rectangles et tels que : BM = DP et DQ = BN. Ces triangles sont donc isométriques (superposables) ; j'en déduis que : QP = MN.
Les côtés opposés du quadrilatère MNPQ sont deux à deux de même longueur, donc MNPQ est un parallélogramme.
Je sais que : AM = PC, que AB = CD (car ABCD est un rectangle) et que : M
 [AB] et P
[AB] et P [CD] ; j'en déduis que : BM = PD.
[CD] ; j'en déduis que : BM = PD.De même, je sais que : BN = DQ, que BC = DA (car ABCD est un rectangle) et que : N
 [BC] et Q
[BC] et Q [DA] ; j'en déduis que : NC = AQ.
[DA] ; j'en déduis que : NC = AQ.Les triangles AMQ et CPN sont rectangles et tels que : AM = CP et AQ = CN. Ces triangles sont donc isométriques (superposables) ; j'en déduis que : MQ = NP.
De même, les triangles BMN et DPQ sont rectangles et tels que : BM = DP et DQ = BN. Ces triangles sont donc isométriques (superposables) ; j'en déduis que : QP = MN.
Les côtés opposés du quadrilatère MNPQ sont deux à deux de même longueur, donc MNPQ est un parallélogramme.
3. a) Aire de MNPQ en fonction de x.
AMNPQ = AABCD − AAMQ − AMBN − ANCP − APDQ = AABCD − 2AAMQ − 2AMBN, d'où :
AMNPQ = 6,5 × 4 − 2 ×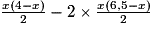 = 26 − (4x − x2) − (6,5x − x2) = 26 − 10,5x + 2x2.
= 26 − (4x − x2) − (6,5x − x2) = 26 − 10,5x + 2x2.
AMNPQ = AABCD − AAMQ − AMBN − ANCP − APDQ = AABCD − 2AAMQ − 2AMBN, d'où :
AMNPQ = 6,5 × 4 − 2 ×
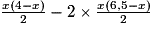 = 26 − (4x − x2) − (6,5x − x2) = 26 − 10,5x + 2x2.
= 26 − (4x − x2) − (6,5x − x2) = 26 − 10,5x + 2x2.b) Cas où x = 0, puis où x = 4.
Si x = 0, MNPQ est confondu avec ABCD ; son aire est donc 4 × 6,5 = 26 cm2.
La formule précédente fournit le même résultat.
Si x = 4, l'aire de MNPQ est de 16 cm2 d'après la question 1.
La formule précédente fournit : 26 − 10,5 × 4 + 2 × 16 = 26 − 42 + 32 = 16 cm2, soit le même résultat.
Si x = 0, MNPQ est confondu avec ABCD ; son aire est donc 4 × 6,5 = 26 cm2.
La formule précédente fournit le même résultat.
Si x = 4, l'aire de MNPQ est de 16 cm2 d'après la question 1.
La formule précédente fournit : 26 − 10,5 × 4 + 2 × 16 = 26 − 42 + 32 = 16 cm2, soit le même résultat.
4. Courbe représentative de l'aire de MNPQ en fonction de x.
Les valeurs de l'aire de MNPQ pour x = 0 et x = 4, à savoir respectivement 26 cm2 et 16 cm2, permettent d'exclure la figure 2.
Par ailleurs, les figures 1 et 4 correspondent à des représentations graphiques de fonctions affines ou affines par morceaux, dont l'expression du premier degré en x (du type : ax + b), ce qui n'est pas le cas de l'expression de l'aire trouvée en 3. a).
La courbe cherchée est donc fournie par la figure 3.
Les valeurs de l'aire de MNPQ pour x = 0 et x = 4, à savoir respectivement 26 cm2 et 16 cm2, permettent d'exclure la figure 2.
Par ailleurs, les figures 1 et 4 correspondent à des représentations graphiques de fonctions affines ou affines par morceaux, dont l'expression du premier degré en x (du type : ax + b), ce qui n'est pas le cas de l'expression de l'aire trouvée en 3. a).
La courbe cherchée est donc fournie par la figure 3.
5. Lecture graphique de l'aire minimale et de la valeur de x correspondante.
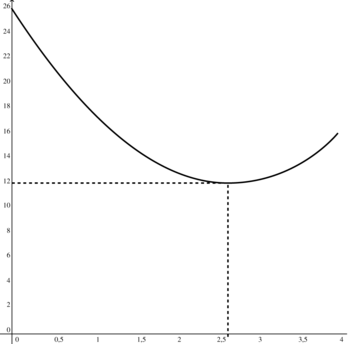 |
Sur le graphique, on lit que l'aire minimale est de 12 cm2, au centimètre carré près, et que la valeur de x correspondante est de 2,5 cm, au demi-centimètre près.
La lecture graphique permet de dire que l'aire minimale est comprise entre 12 cm2 et 13 cm2, on peut donc dire que l'aire vaut 12 ou 13, au centimètre carré près.
De même, on lit sur le graphique que la valeur de x correspondante est comprise entre 2,5 cm et 3 cm, on peut donc répondre en donnant les valeurs 2,5 ou 3, au choix.
L'usage (et le souci de précision) veut que l'on donne la valeur qui semble la plus proche, mais les deux réponses sont valides, au vu de la question.
La lecture graphique permet de dire que l'aire minimale est comprise entre 12 cm2 et 13 cm2, on peut donc dire que l'aire vaut 12 ou 13, au centimètre carré près.
De même, on lit sur le graphique que la valeur de x correspondante est comprise entre 2,5 cm et 3 cm, on peut donc répondre en donnant les valeurs 2,5 ou 3, au choix.
L'usage (et le souci de précision) veut que l'on donne la valeur qui semble la plus proche, mais les deux réponses sont valides, au vu de la question.
6. a) Formule pour la cellule B2.
Il est tout d'abord à noter que les points de suspension mentionnés en colonne O n'ont aucun sens dans un environnement « tableur ». Ce qu'il faut en comprendre, c'est qu'après la colonne N, on poursuit en faisant augmenter x de 0,1 par colonne.
La colonne correspondant à la valeur x = 3,8 ne sera pas la colonne P…
De notre point de vue, il eut mieux valu laisser le tableau ouvert sur la droite en ne mentionnant plus de référence aux colonnes.
Pour pouvoir compléter la ligne 2 en recopiant la cellule B2 vers la droite, on peut entrer la formule suivante en B2 : « =25−10*B1+2*B1(accent circonflexe)2 » ou : « =25−10*B1+2*B1*B1 ».
Il est tout d'abord à noter que les points de suspension mentionnés en colonne O n'ont aucun sens dans un environnement « tableur ». Ce qu'il faut en comprendre, c'est qu'après la colonne N, on poursuit en faisant augmenter x de 0,1 par colonne.
La colonne correspondant à la valeur x = 3,8 ne sera pas la colonne P…
De notre point de vue, il eut mieux valu laisser le tableau ouvert sur la droite en ne mentionnant plus de référence aux colonnes.
Pour pouvoir compléter la ligne 2 en recopiant la cellule B2 vers la droite, on peut entrer la formule suivante en B2 : « =25−10*B1+2*B1(accent circonflexe)2 » ou : « =25−10*B1+2*B1*B1 ».
b) Valeur approchée de l'aire minimale à 0,1 cm2 près.
La réponse attendue était certainement la suivante :
Dire que la valeur minimale de l'aire à 0,1 cm2 est 12,22 signifie que cette aire est comprise entre 12,12 et 12,32. Les valeurs fournies par le tableau ne permettent pas d'exclure la possibilité que pour une (des) valeur(s) de x comprise(s) entre 2,5 et 2,6 ou entre 2,6 et 2,7 l'aire prenne une (des) valeur(s) inférieure(s) à 12,12.
La réponse attendue était certainement la suivante :
Dire que la valeur minimale de l'aire à 0,1 cm2 est 12,22 signifie que cette aire est comprise entre 12,12 et 12,32. Les valeurs fournies par le tableau ne permettent pas d'exclure la possibilité que pour une (des) valeur(s) de x comprise(s) entre 2,5 et 2,6 ou entre 2,6 et 2,7 l'aire prenne une (des) valeur(s) inférieure(s) à 12,12.
7. Montrons que l'on peut exprimer l'aire sous la forme : 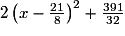 .
.
Lorsqu'il faut démontrer une égalité, on part du membre le plus complexe, que l'on réduit et simplifie jusqu'à obtenir le membre le plus simple. Si les deux membres de l'égalité sont complexes, on les réduit et simplifie séparément, jusqu'à converger vers un résultat commun.
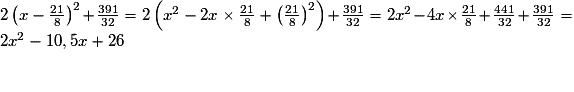
Ceci correspond à l'expression de l'aire trouvée en 3.
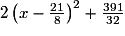 .
.Lorsqu'il faut démontrer une égalité, on part du membre le plus complexe, que l'on réduit et simplifie jusqu'à obtenir le membre le plus simple. Si les deux membres de l'égalité sont complexes, on les réduit et simplifie séparément, jusqu'à converger vers un résultat commun.
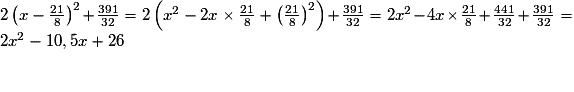
Ceci correspond à l'expression de l'aire trouvée en 3.
Calcul de l'aire minimale et de la valeur de x correspondante.
L'expression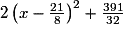 est toujours positive et est la somme de deux termes toujours positifs, dont le deuxième est constant.
est toujours positive et est la somme de deux termes toujours positifs, dont le deuxième est constant.
Cette expression sera minimale lorsque le premier terme est nul, ce qui est le cas lorsque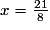 , c'est-à-dire : 2,625 (cm).
, c'est-à-dire : 2,625 (cm).
L'aire vaut alors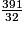 , soit : 12,21875 (cm2).
, soit : 12,21875 (cm2).
L'expression
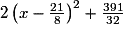 est toujours positive et est la somme de deux termes toujours positifs, dont le deuxième est constant.
est toujours positive et est la somme de deux termes toujours positifs, dont le deuxième est constant.Cette expression sera minimale lorsque le premier terme est nul, ce qui est le cas lorsque
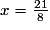 , c'est-à-dire : 2,625 (cm).
, c'est-à-dire : 2,625 (cm).L'aire vaut alors
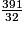 , soit : 12,21875 (cm2).
, soit : 12,21875 (cm2).Exercice 2
Dans cet exercice, il est demandé au candidat d'indiquer, en justifiant, si des affirmations sont vraies ou fausses. Certaines de ces affirmations sont contextualisées ; il faut donc bien prendre le temps de lire attentivement les indications fournies.
Pour justifier qu'une affirmation est fausse, on peut, selon les cas : résoudre l'exercice et trouver un résultat autre que celui qui est annoncé, fournir un contre-exemple, démontrer que la proposition est fausse en prouvant un résultat incompatible avec celui proposé.
Pour prouver qu'une proposition est vraie, on peut résoudre l'exercice et trouver le résultat annoncé ou démontrer la vérité générale de la proposition, en utilisant des propriétés connues.
Pour justifier qu'une affirmation est fausse, on peut, selon les cas : résoudre l'exercice et trouver un résultat autre que celui qui est annoncé, fournir un contre-exemple, démontrer que la proposition est fausse en prouvant un résultat incompatible avec celui proposé.
Pour prouver qu'une proposition est vraie, on peut résoudre l'exercice et trouver le résultat annoncé ou démontrer la vérité générale de la proposition, en utilisant des propriétés connues.
1. Affirmation 1 : En 5 ans, les prix ont augmenté de 50 %.
Si n est le prix initial, au bout d'un an, le prix est :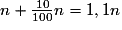 .
.
La deuxième année, le prix devient : (1,1n) × 1,1 = 1,12n.
Au bout de cinq années de cette même augmentation, le prix est devenu : 1,15n = 1,61051n ce qui correspond à une augmentation de plus de 61 %.
L'affirmation 1 est fausse.
Si n est le prix initial, au bout d'un an, le prix est :
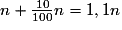 .
.La deuxième année, le prix devient : (1,1n) × 1,1 = 1,12n.
Au bout de cinq années de cette même augmentation, le prix est devenu : 1,15n = 1,61051n ce qui correspond à une augmentation de plus de 61 %.
L'affirmation 1 est fausse.
2. Affirmation 2 : Une boisson comportant 5 volumes de sirop de fraise pour 9 volumes d'eau est plus sucrée qu'une boisson comportant 4 volumes de sirop de fraise pour 7 volumes d'eau.
Cette question relève d'une catégorie de problème appelé : « comparaison de proportions ». Nous mentionnons ici deux procédures possibles de résolution, parmi d'autres…
Cette question relève d'une catégorie de problème appelé : « comparaison de proportions ». Nous mentionnons ici deux procédures possibles de résolution, parmi d'autres…
1ère procédure : j'exprime la fraction de sirop de fraise par rapport au volume total dans les deux cas, puis je compare les fractions.
Le premier mélange comporte 5 volumes de sirop de fraise pour 9 volumes d'eau ; le volume de sirop de fraise représente donc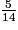 du total.
du total.
Le deuxième mélange comporte 4 volumes de sirop de fraise pour 7 volumes d'eau ; le volume de sirop de fraise représente donc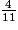 du total.
du total.
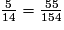 et
et 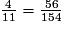 donc
donc 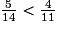 . Le second mélange est plus sucré.
. Le second mélange est plus sucré.
L'affirmation 2 est fausse.
Le premier mélange comporte 5 volumes de sirop de fraise pour 9 volumes d'eau ; le volume de sirop de fraise représente donc
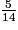 du total.
du total.Le deuxième mélange comporte 4 volumes de sirop de fraise pour 7 volumes d'eau ; le volume de sirop de fraise représente donc
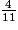 du total.
du total.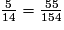 et
et 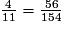 donc
donc 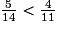 . Le second mélange est plus sucré.
. Le second mélange est plus sucré.L'affirmation 2 est fausse.
2e procédure : je compare les deux mélanges à volume d'eau égal.
9 et 7 ont pour multiple commun 63. Je calcule, dans les deux cas, le volume de sirop de fraise pour 63 volumes d'eau.
Pour le premier mélange, pour 63 = 9 × 7 volumes d'eau, il faudra : 5 × 7 = 35 volumes de sirop de fraise ; pour le second mélange, pour 63 = 7 × 9 volumes d'eau, il faudra : 4 × 9 = 36 volumes de sirop de fraise. Le second mélange est donc plus sucré que le premier.
L'affirmation 2 est fausse.
9 et 7 ont pour multiple commun 63. Je calcule, dans les deux cas, le volume de sirop de fraise pour 63 volumes d'eau.
Pour le premier mélange, pour 63 = 9 × 7 volumes d'eau, il faudra : 5 × 7 = 35 volumes de sirop de fraise ; pour le second mélange, pour 63 = 7 × 9 volumes d'eau, il faudra : 4 × 9 = 36 volumes de sirop de fraise. Le second mélange est donc plus sucré que le premier.
L'affirmation 2 est fausse.
3. Affirmation 3 : On a autant de chances d'obtenir un nombre pair qu'un nombre impair.
Calculons la valeur de p. Le total des probabilités de toutes les issues d'un événement vaut toujours 1.
On a donc :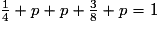 d'où
d'où 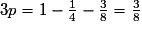 et
et 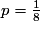 .
.
La probabilité d'obtenir un nombre pair est : p(2) + p(4) =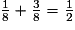 .
.
Celle d'obtenir un nombre impair vaut donc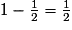 .
.
L'affirmation 3 est vraie.
Calculons la valeur de p. Le total des probabilités de toutes les issues d'un événement vaut toujours 1.
On a donc :
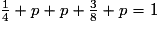 d'où
d'où 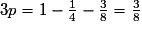 et
et 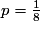 .
.La probabilité d'obtenir un nombre pair est : p(2) + p(4) =
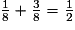 .
.Celle d'obtenir un nombre impair vaut donc
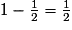 .
.L'affirmation 3 est vraie.
4. Affirmation 4 : La différence entre les carrés de deux nombres entiers naturels consécutifs est égale à la somme de ces deux nombres entiers.
Soient n et n + 1 deux nombres entiers naturels consécutifs.
La différence des carrés de ces deux nombres est : (n + 1)2 − n2.
On admet que la différence est forcément positive, c'est-à-dire que l'on soustrait le plus petit des deux nombres au plus grand.
Or (n + 1)2 − n2 = n2 + 2n + 1 − n2 = 2n + 1 = n + (n + 1).
L'affirmation 4 est vraie.
Soient n et n + 1 deux nombres entiers naturels consécutifs.
La différence des carrés de ces deux nombres est : (n + 1)2 − n2.
On admet que la différence est forcément positive, c'est-à-dire que l'on soustrait le plus petit des deux nombres au plus grand.
Or (n + 1)2 − n2 = n2 + 2n + 1 − n2 = 2n + 1 = n + (n + 1).
L'affirmation 4 est vraie.
5. Affirmation 5 : Si on augmente l'arête d'un cube de 10 %, alors le volume de ce cube augmente de 33,1 %.
Rappel : Par agrandissement ou réduction de rapport k, les distances sont multipliées par k, les aires par k2 et les volumes par k3.
Si on augmente l'arête d'un cube de 10, cela signifie que l'on multiplie la longueur de l'arête par 1,1. Le volume est donc multiplié par 1,13 = 1,331. Cela correspond à une augmentation du volume de 33,1 %.
L'affirmation 5 est vraie.
Rappel : Par agrandissement ou réduction de rapport k, les distances sont multipliées par k, les aires par k2 et les volumes par k3.
Si on augmente l'arête d'un cube de 10, cela signifie que l'on multiplie la longueur de l'arête par 1,1. Le volume est donc multiplié par 1,13 = 1,331. Cela correspond à une augmentation du volume de 33,1 %.
L'affirmation 5 est vraie.
6. Affirmation 6 : Sans la technique « de l'œuf », la vitesse moyenne du skieur est de 60 km/h.
Supposons que la vitesse moyenne du skieur soit de 60 km/h. La position « de l'œuf » permet d'accroître cette vitesse de 50 %, ce qui signifie que le skieur atteindra une vitesse de 60 × 1,5 = 90 km/h, et non pas 120 km/h.
Un skieur qui atteint une vitesse de 120 km/h en position « de l'œuf » a donc une vitesse supérieure à 60 km/h en position « normale »…
L'affirmation 6 est fausse.
Supposons que la vitesse moyenne du skieur soit de 60 km/h. La position « de l'œuf » permet d'accroître cette vitesse de 50 %, ce qui signifie que le skieur atteindra une vitesse de 60 × 1,5 = 90 km/h, et non pas 120 km/h.
Un skieur qui atteint une vitesse de 120 km/h en position « de l'œuf » a donc une vitesse supérieure à 60 km/h en position « normale »…
L'affirmation 6 est fausse.
On procède ici à un raisonnement par l'absurde : on part de la conclusion pour montrer qu'elle mène à une contradiction avec les données de l'énoncé.
7. Affirmation 7 : Si AB = n et AH = 1, alors AC = 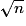 .
.
Le triangle BHC est rectangle en H, donc d'après le théorème de Pythagore : BH2 + HC2 = BC2 d'où BC2 = (n − 1)2 + HC2.
Le triangle AHC est rectangle en H, donc d'après le théorème de Pythagore : AH2 + HC2 = AC2 d'où HC2 = AC2 − 1.
En remplaçant dans l'égalité précédente, il vient : BC2 = (n − 1)2 + HC2 = (n − 1)2 + AC2 − 1.
Comme C est sur le demi-cercle de diamètre [AB], le triangle ABC est rectangle en C. On a donc, d'après le théorème de Pythagore : AB2 = AC2 + CB2.
En remplaçant CB2 par l'expression obtenue ci-dessus, il vient : AB2 = AC2 + (n − 1)2 + AC2 − 1 d'où n2 = 2AC2 + n2 − 2n + 1 − 1 et donc 2AC2 = 2n.
Finalement : AC =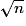 .
.
L'affirmation 7 est vraie.
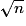 .
.Le triangle BHC est rectangle en H, donc d'après le théorème de Pythagore : BH2 + HC2 = BC2 d'où BC2 = (n − 1)2 + HC2.
Le triangle AHC est rectangle en H, donc d'après le théorème de Pythagore : AH2 + HC2 = AC2 d'où HC2 = AC2 − 1.
En remplaçant dans l'égalité précédente, il vient : BC2 = (n − 1)2 + HC2 = (n − 1)2 + AC2 − 1.
Comme C est sur le demi-cercle de diamètre [AB], le triangle ABC est rectangle en C. On a donc, d'après le théorème de Pythagore : AB2 = AC2 + CB2.
En remplaçant CB2 par l'expression obtenue ci-dessus, il vient : AB2 = AC2 + (n − 1)2 + AC2 − 1 d'où n2 = 2AC2 + n2 − 2n + 1 − 1 et donc 2AC2 = 2n.
Finalement : AC =
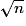 .
.L'affirmation 7 est vraie.
Exercice 3
1. Construction de l'ove.
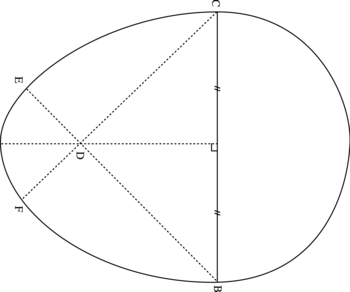 |
2. Calcul du périmètre de l'ove.
Observons tout d'abord la figure. L'ove est constitué :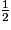 π × 10 = 5π ;
π × 10 = 5π ;
p2 = p3 =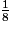 π × 20 = 2,5π et p4 =
π × 20 = 2,5π et p4 = 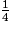 π × 2 × (10 −
π × 2 × (10 − 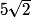 ) = 5π −
) = 5π − 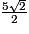 π.
π.
On obtient : p = 5π + 2 × 2,5π + 5π −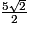 π = 15π −
π = 15π − 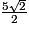 π.
π.
P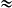 36 cm à 0,1 cm près.
36 cm à 0,1 cm près.
Observons tout d'abord la figure. L'ove est constitué :
- d'un demi-cercle de longueur p1 de diamètre BC = 10 cm ;
- d'un arc de cercle de rayon BC et de centre B tel que l'angle au centre soit égal à 45°. En effet, le triangle BDC étant rectangle et isocèle en D, on a :
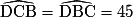 . Il s'agit donc d'un huitième de cercle ; notons p2 sa longueur ;
. Il s'agit donc d'un huitième de cercle ; notons p2 sa longueur ; - d'un arc de cercle de rayon BC et de centre C tel que l'angle au centre soit égal à 45°. La longueur p3 de cet arc est égale à p2 ;
- d'un quart de cercle de centre D et de rayon DE, de longueur notée p4. On remarque que B, D et E étant alignés dans cet ordre, DE = BE − BD. Or BE = BC = 10 et BD est le côté d'un triangle isocèle et rectangle d'hypoténuse 10 ; le théorème de Pythagore permet d'établir que
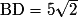 ; d'où :
; d'où : 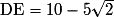 .
.
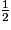 π × 10 = 5π ;
π × 10 = 5π ;p2 = p3 =
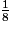 π × 20 = 2,5π et p4 =
π × 20 = 2,5π et p4 = 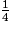 π × 2 × (10 −
π × 2 × (10 − 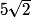 ) = 5π −
) = 5π − 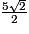 π.
π.On obtient : p = 5π + 2 × 2,5π + 5π −
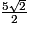 π = 15π −
π = 15π − 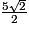 π.
π.P
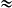 36 cm à 0,1 cm près.
36 cm à 0,1 cm près.