Dernier essai le
- Score :
/20
Angle
Soit un point O et deux demi-droites [Ox) et [Oy) issues de ce point. Ces deux demi-droites définissent deux secteurs angulaires ou plus simplement deux angles : un angle saillant 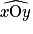 et un angle rentrant
et un angle rentrant 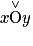 . Ceux-ci ont pour sommet O et pour côtés [Ox) et [Oy).
. Ceux-ci ont pour sommet O et pour côtés [Ox) et [Oy).
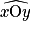
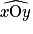 et un angle rentrant
et un angle rentrant 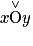 . Ceux-ci ont pour sommet O et pour côtés [Ox) et [Oy).
. Ceux-ci ont pour sommet O et pour côtés [Ox) et [Oy).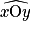
Remarque
Le mot angle désigne également la grandeur du secteur angulaire (sa plus ou moins grande ouverture). L'unité d'angle la plus utilisée au collège est le degré.
Angle inscrit
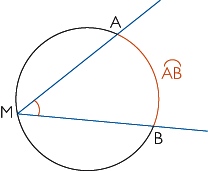 |
Soit A, B et M trois points distincts d'un cercle. L'angle 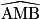 est appelé angle inscrit dans ce cercle. On dit que cet angle intercepte l'arc est appelé angle inscrit dans ce cercle. On dit que cet angle intercepte l'arc 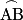 . . |
Propriété
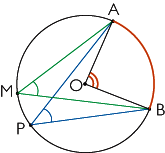 |
| Deux angles inscrits interceptant le même arc ont la même mesure. Sur la figure ci-contre, les angles inscrits 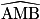 et et  interceptent le même arc interceptent le même arc 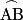 . .On en déduit que 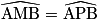 . . |
Angles adjacents
Deux angles sont adjacents s'ils :
- ont le même sommet,
- ont un côté commun,
- sont situés de part et d'autre de ce côté commun.
Exemple
Les angles 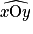 et
et 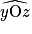 représentés ci-dessous sont adjacents.
représentés ci-dessous sont adjacents.
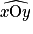 et
et 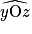 représentés ci-dessous sont adjacents.
représentés ci-dessous sont adjacents.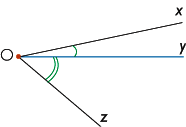 |
Angles alternes-internes
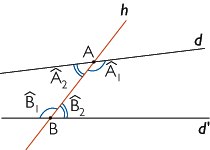
Soit deux droites d et d' et une autre droite h qui coupe d et d' en deux points A et B. Deux angles qui sont disposés de part et d'autre de h et situés à l'intérieur de la surface comprise entre d et d' sont dits alternes-internes.
Exemple
Les angles 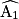 et
et 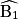 représentés ci-dessous sont alternes-internes ; de même, les angles
représentés ci-dessous sont alternes-internes ; de même, les angles 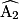 et
et 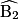 .
.
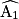 et
et 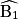 représentés ci-dessous sont alternes-internes ; de même, les angles
représentés ci-dessous sont alternes-internes ; de même, les angles 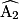 et
et 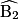 .
. |
Propriété
Si d et d' sont parallèles, alors deux angles alternes internes par rapport à d et d' sont égaux.
Angles complémentaires, angles supplémentaires
Deux angles sont complémentaires si la somme de leurs mesures est égale à 90°. Par exemple, le complémentaire d'un angle de 47° est un angle de 43°, car 47° + 43° = 90°.
Deux angles sont supplémentaires si la somme de leurs mesures est égale à 180°. Par exemple, le supplémentaire d'un angle de 47° est un angle de 133°, car 47° + 133° = 180°.
Angles correspondants
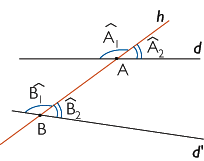
Soit deux droites d et d' et une autre droite h qui coupe d et d' en deux points A et B. Deux angles qui sont disposés du même côté de h, l'un situé à l'intérieur de la surface comprise entre d et d', l'autre à l'extérieur sont dits correspondants.
Exemple
Les angles 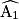 et
et 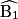 représentés ci-dessous sont correspondants ; de même, les angles
représentés ci-dessous sont correspondants ; de même, les angles 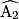 et
et 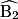 .
.
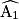 et
et 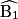 représentés ci-dessous sont correspondants ; de même, les angles
représentés ci-dessous sont correspondants ; de même, les angles 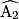 et
et 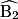 .
. |
Propriété
Si d et d' sont parallèles alors deux angles correspondants par rapport à d et d' sont égaux.
cosinus d'un angle aigu
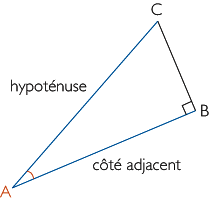 |
Soit ABC un triangle rectangle en B. On appelle cosinus de l'angle aigu 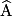 le rapport le rapport 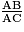 . On écrit : . On écrit : 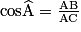 . . |
Pour mémoriser la formule, on écrit : 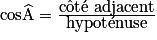 , où côté adjacent signifie « côté adjacent à l'angle
, où côté adjacent signifie « côté adjacent à l'angle 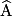 , qui n'est pas l'hypoténuse ».
, qui n'est pas l'hypoténuse ».
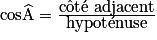 , où côté adjacent signifie « côté adjacent à l'angle
, où côté adjacent signifie « côté adjacent à l'angle 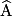 , qui n'est pas l'hypoténuse ».
, qui n'est pas l'hypoténuse ».Remarque
Le cosinus d'un angle aigu est compris entre 0 et 1, car l'hypoténuse d'un triangle rectangle est le plus grand des trois côtés.
Voici quelques valeurs particulières :
angle 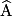 | 30° | 45° | 60° |
cos 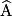 | 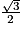 | 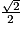 | 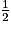 |
Sinus d'un angle aigu
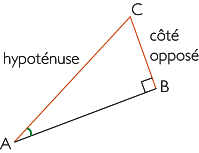 |
Soit ABC un triangle rectangle en B. On appelle sinus de l'angle aigu  le rapport de longueurs 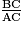 . On écrit : . On écrit : 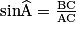 . . |
Pour mémoriser la formule, on écrit : 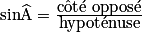 , où côté opposé signifie « côté opposé à l'angle  ».
, où côté opposé signifie « côté opposé à l'angle  ».
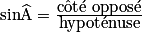 , où côté opposé signifie « côté opposé à l'angle  ».
, où côté opposé signifie « côté opposé à l'angle  ».Remarque
Le sinus d'un angle aigu d'un triangle rectangle est l'un des trois rapports trigonométriques permettant de caractériser un triangle rectangle.
Le sinus d'un angle aigu est compris entre 0 et 1 car l'hypoténuse d'un triangle rectangle est le plus grand des trois côtés.
Voici quelques valeurs particulières :
| angle  | 30° | 45° | 60° |
| sin  | 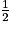 | 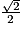 | 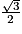 |
Tangente d'un angle aigu
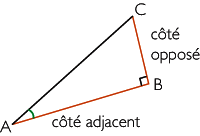 |
Soit ABC un triangle rectangle en B. On appelle tangente de l'angle aigu 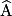 le rapport le rapport 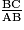 . On écrit : . On écrit : 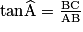 . . |
Pour mémoriser la formule, on écrit : 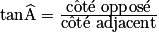 , où côté opposé signifie « côté opposé à l'angle  » et côté adjacent, « côté adjacent à l'angle Â, qui n'est pas l'hypoténuse ».
, où côté opposé signifie « côté opposé à l'angle  » et côté adjacent, « côté adjacent à l'angle Â, qui n'est pas l'hypoténuse ».
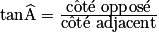 , où côté opposé signifie « côté opposé à l'angle  » et côté adjacent, « côté adjacent à l'angle Â, qui n'est pas l'hypoténuse ».
, où côté opposé signifie « côté opposé à l'angle  » et côté adjacent, « côté adjacent à l'angle Â, qui n'est pas l'hypoténuse ».Remarque
La tangente d'un angle aigu d'un triangle rectangle est l'un des trois rapports trigonométriques permettant de caractériser un triangle rectangle.
Document précédent
Les volumes
Document suivant
Les transformations d'unités
