Dernier essai le
- Score :
/20
Énoncé
Énoncé
Sujet
• Ce sujet comporte deux parties indépendantes, l’une en français et l’autre en mathématiques
• La durée de traitement par le candidat de chacune des parties est estimée à 2 heures.
• Les barèmes indicatifs sont établis sur 20 points pour chaque partie.
• S’agissant de la note finale pour l’épreuve, elle sera composée d’une note sur 10 pour chaque partie. Une note inférieure à 2,5 sur 10 à l’une des parties est éliminatoire.
Corrigé
Corrigé
Exercice 1 (4 points)
1.
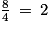
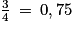
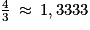
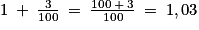
Ainsi, on a :
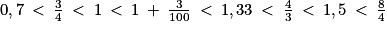
2.
a.
a.
Dans la liste des huit nombres donnés, les nombres entiers sont 1 et 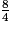 (car
(car 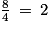 ).
).
L'expérience aléatoire est ici « choisir un nombre de la liste au hasard ».
L'univers associé est l'ensemble des huit nombres.
Soit A l'événement « le nombre choisi est un nombre entier ».
L'événement A est composé (on dit aussi réalisé) de deux issues : 1 et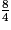 .
.
Comme on estime que chaque nombre a autant de chance d'être choisi qu'un autre, on est dans une situation d'équiprobabilité. On utilise donc la formule suivante :
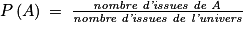
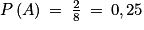
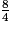 (car
(car 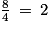 ).
).L'expérience aléatoire est ici « choisir un nombre de la liste au hasard ».
L'univers associé est l'ensemble des huit nombres.
Soit A l'événement « le nombre choisi est un nombre entier ».
L'événement A est composé (on dit aussi réalisé) de deux issues : 1 et
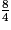 .
.Comme on estime que chaque nombre a autant de chance d'être choisi qu'un autre, on est dans une situation d'équiprobabilité. On utilise donc la formule suivante :
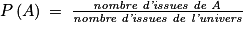
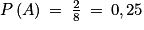
2.
b.
b.
Un nombre décimal est un nombre qui peut s'écrire comme le quotient d'un nombre entier par une puissance de 10.
0,7 est décimal car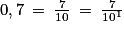 .
.
0,75 est décimal car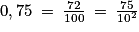 .
.
1 est décimal car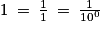 . On peut aussi utiliser le fait que tout nombre entier est un nombre décimal (la réciproque de cette affirmation est évidemment fausse : 0,7 est décimal mais non entier).
. On peut aussi utiliser le fait que tout nombre entier est un nombre décimal (la réciproque de cette affirmation est évidemment fausse : 0,7 est décimal mais non entier).
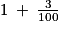 est décimal car
est décimal car 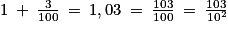 .
.
1,33 est décimal car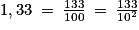 .
.
1,5 est décimal car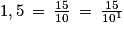 .
.
Enfin,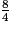 est décimal car
est décimal car 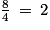 et tout entier est décimal.
et tout entier est décimal.
Soit B l'événement « le nombre choisi est un nombre décimal ».
L'événement B est ainsi composé de sept issues.
L'expérience aléatoire étant la même, on a ainsi par la formule précédente :
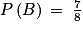
0,7 est décimal car
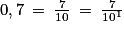 .
.0,75 est décimal car
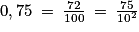 .
.1 est décimal car
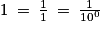 . On peut aussi utiliser le fait que tout nombre entier est un nombre décimal (la réciproque de cette affirmation est évidemment fausse : 0,7 est décimal mais non entier).
. On peut aussi utiliser le fait que tout nombre entier est un nombre décimal (la réciproque de cette affirmation est évidemment fausse : 0,7 est décimal mais non entier).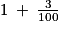 est décimal car
est décimal car 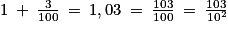 .
.1,33 est décimal car
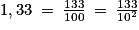 .
.1,5 est décimal car
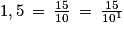 .
.Enfin,
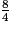 est décimal car
est décimal car 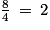 et tout entier est décimal.
et tout entier est décimal.Soit B l'événement « le nombre choisi est un nombre décimal ».
L'événement B est ainsi composé de sept issues.
L'expérience aléatoire étant la même, on a ainsi par la formule précédente :
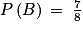
Exercice 2 (5 points)
1.
a.
a.
On va calculer le prix pour 4 visites.
Formule A : 45 × 4 = 180 €
Formule B : 90 + 25,5 × 4 = 192 €
Formule C : 300 €
Ainsi, pour quatre visites, il est plus avantageux de choisir la formule A.
Formule A : 45 × 4 = 180 €
Formule B : 90 + 25,5 × 4 = 192 €
Formule C : 300 €
Ainsi, pour quatre visites, il est plus avantageux de choisir la formule A.
b.
On va calculer le prix pour 8 visites (deux visites par classe).
Formule A : 45 × 8 = 360 €
Formule B : 90 + 25,5 × 8 = 294 €
Formule C : 300 €
Ainsi, pour huit visites, il est plus avantageux de choisir la formule B.
Formule A : 45 × 8 = 360 €
Formule B : 90 + 25,5 × 8 = 294 €
Formule C : 300 €
Ainsi, pour huit visites, il est plus avantageux de choisir la formule B.
2.
Soit v le nombre de visites effectuées.
En choisissant la formule B, on va alors payer : 90 + 25,5 × v €.
En choisissant la formule C, on va payer : 300 €.
La formule C est plus économique que la B lorsque le montant de 300 € est inférieur au montant de 90 + 25,5 × v €.
On cherche donc le plus petit entier v tel que :
300 90 + 25,5 × v
90 + 25,5 × v
Il faut isoler l'inconnue v dans cette inégalité.
On soustrait les deux membres par 90 (le symbole ne change pas de sens) :
300 − 90 90 + 25,5 × v − 90
90 + 25,5 × v − 90
210 25,5v
25,5v
On peut réécrire l'inégalité de cette manière, afin d'avoir l'inconnue v à gauche de l'inégalité :
25,5v 210
210
On divise les deux membres par 25,5 (le symbole ne change pas de sens car 25,5 > 0) :
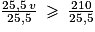
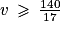
Or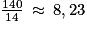 .
.
Donc le plus petit entier recherché est 9.
Ainsi, à partir de neuf visites, la formule C sera plus économique que la formule B.
(On peut le vérifier en calculant 90 + 25,5 × 9 = 319,5 € ; on a bien 300 < 319,5).
En choisissant la formule B, on va alors payer : 90 + 25,5 × v €.
En choisissant la formule C, on va payer : 300 €.
La formule C est plus économique que la B lorsque le montant de 300 € est inférieur au montant de 90 + 25,5 × v €.
On cherche donc le plus petit entier v tel que :
300
 90 + 25,5 × v
90 + 25,5 × vIl faut isoler l'inconnue v dans cette inégalité.
On soustrait les deux membres par 90 (le symbole ne change pas de sens) :
300 − 90
 90 + 25,5 × v − 90
90 + 25,5 × v − 90210
 25,5v
25,5vOn peut réécrire l'inégalité de cette manière, afin d'avoir l'inconnue v à gauche de l'inégalité :
25,5v
 210
210On divise les deux membres par 25,5 (le symbole ne change pas de sens car 25,5 > 0) :
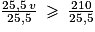
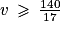
Or
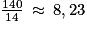 .
.Donc le plus petit entier recherché est 9.
Ainsi, à partir de neuf visites, la formule C sera plus économique que la formule B.
(On peut le vérifier en calculant 90 + 25,5 × 9 = 319,5 € ; on a bien 300 < 319,5).
3.
La formule C est représentée par la droite rouge (parallèle à l'axe des abscisses) car, quel que soit le nombre de visites effectuées, le prix sera de 300 €.
La formule A est représentée par la droite bleue, car pour aucune visite (0 visite), alors le prix sera de 0 €. Et seule la droite bleue passe par l'origine du repère (le point de coordonnées (0 ;0)).
Ainsi, la formule B est représentée par la droite verte.
La formule A est représentée par la droite bleue, car pour aucune visite (0 visite), alors le prix sera de 0 €. Et seule la droite bleue passe par l'origine du repère (le point de coordonnées (0 ;0)).
Ainsi, la formule B est représentée par la droite verte.
Remarque : il est surprenant que la représentation graphique des formules soit des droites et non pas un ensemble de points alignés, car le nombre de visites est un nombre entier – on ne peut pas effectuer 1,3 visite, par exemple.
Pour déterminer le nombre de visites à effectuer pour que la formule B soit plus économique que la formule A, on détermine sur l'axe des abscisses le nombre de visites à partir duquel la droite verte est située en dessous de la droite bleue. L'ensemble solution est 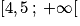 (avec la précision de la représentation graphique). Le nombre de visites étant un nombre entier, on peut donc affirmer qu'à partir de cinq visites, il est plus économique de choisir la formule B.
(avec la précision de la représentation graphique). Le nombre de visites étant un nombre entier, on peut donc affirmer qu'à partir de cinq visites, il est plus économique de choisir la formule B.
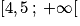 (avec la précision de la représentation graphique). Le nombre de visites étant un nombre entier, on peut donc affirmer qu'à partir de cinq visites, il est plus économique de choisir la formule B.
(avec la précision de la représentation graphique). Le nombre de visites étant un nombre entier, on peut donc affirmer qu'à partir de cinq visites, il est plus économique de choisir la formule B.4.
Les 15 % de subvention désignent ici une proportion et non pas une évolution (augmentation ou diminution).
La formule B étant la plus avantageuse pour 8 visites, le prix à payer est de 294 € avant subvention. Le montant de la subvention se calcule ainsi :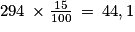 .
.
On calcule maintenant le montant restant à payer : 294 − 44,1 = 249,9.
Ainsi, l'école devra régler 249,90 €.
La formule B étant la plus avantageuse pour 8 visites, le prix à payer est de 294 € avant subvention. Le montant de la subvention se calcule ainsi :
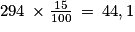 .
.On calcule maintenant le montant restant à payer : 294 − 44,1 = 249,9.
Ainsi, l'école devra régler 249,90 €.
Exercice 3 (4 points)
1.
L'aire d'un carré est égale au carré de la longueur de ses côtés : Acarré = c × c = 8 × 8 = 64.
L'aire du carré est donc de 64 cm2.
L'aire du carré est donc de 64 cm2.
2.
Agrisée = Acarré−Ablanche
La surface blanche est constituée de deux demi-disques de diamètre 8 cm et donc de rayon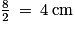 .
.
L'aire d'un disque de rayon r est égale à π × r2.
Ainsi, l'aire d'un demi-disque de rayon r est égale à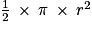 .
.
Donc :
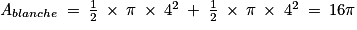
Ainsi :
Agrisée = 64 − 16π
Agrisée 13,73
13,73
Ainsi, la surface grisée a pour aire exacte 64 − 16π cm2 soit environ 13,73 cm2.
La surface blanche est constituée de deux demi-disques de diamètre 8 cm et donc de rayon
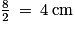 .
.L'aire d'un disque de rayon r est égale à π × r2.
Ainsi, l'aire d'un demi-disque de rayon r est égale à
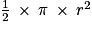 .
.Donc :
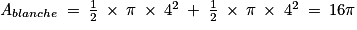
Ainsi :
Agrisée = 64 − 16π
Agrisée
 13,73
13,73Ainsi, la surface grisée a pour aire exacte 64 − 16π cm2 soit environ 13,73 cm2.
Remarque : pour le calcul de l'aire de la surface blanche, on pouvait aussi remarquer que les deux demi-disques possèdent ensemble la même aire qu'un disque complet.
On pouvait donc calculer directement :
Ablanche = π × 42 = 16π
Ablanche = π × 42 = 16π
Des rappels sur les propriétés des cercles et des disques peuvent être téléchargés sur le site de l'académie de Versailles.
3.
Une échelle de a:b signifie que a cm représente b cm.
Une échelle de 125: 1 signifie que 125 cm sur le sol de la cour représentent 1 cm sur le schéma initial.
Une échelle de 125: 1 signifie que 125 cm sur le sol de la cour représentent 1 cm sur le schéma initial.
a.
La longueur des côtés du carré sur le sol de la cour sera donc de 125 × 8 = 1 000 cm.
Puis, à l'aide d'un tableau de conversion :
On a 1 000 cm = 10 m.
Puis, à l'aide d'un tableau de conversion :
| dam | m | dm | cm | mm |
| 1 | 0 | 0 | 0 | |
On a 1 000 cm = 10 m.
b.
On peut nommer les quatre sommets du carré sur le sol de la cour : A, B, C et D.
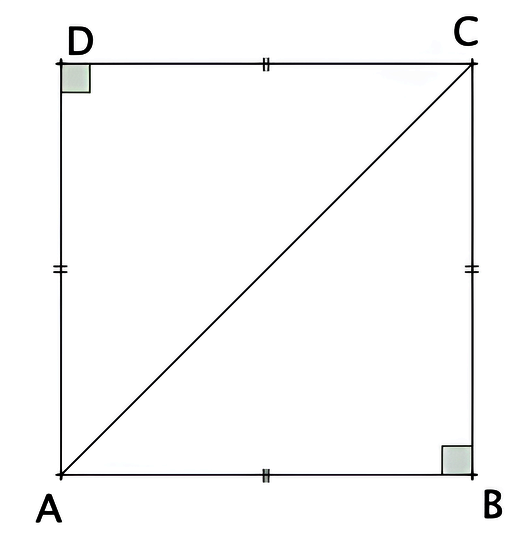 |
Pour calculer la longueur de la diagonale [AC], on peut utiliser le théorème de Pythagore dans le triangle rectangle ABC.
On a :
AC2 = AB2+BC2
AC2 = 102 + 102
AC2 = 200
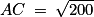
AC 14,14
14,14
Ainsi, le carré qui sera dessiné sur le sol de la cour aura une diagonale d'environ 14,14 m.
On a :
AC2 = AB2+BC2
AC2 = 102 + 102
AC2 = 200
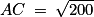
AC
 14,14
14,14Ainsi, le carré qui sera dessiné sur le sol de la cour aura une diagonale d'environ 14,14 m.
Remarque : il était également possible de raisonner en utilisant la trigonométrie dans le triangle rectangle ABC. En effet, comme ce triangle est isocèle rectangle en B, on a donc l'angle 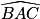 qui mesure 45°.
qui mesure 45°.
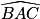 qui mesure 45°.
qui mesure 45°.Étant donné que l'on recherche la longueur du segment [AC], on peut utiliser la formule du cosinus. On a :
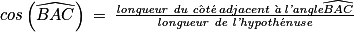
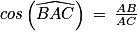
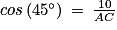
La valeur cos(45°) est une valeur remarquable.
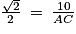
En utilisant la proportionnalité, on a :
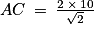
Afin de simplifier la fraction, on peut écrire que 2 est égal à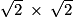
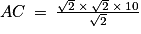
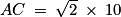
On peut écrire que 10 est égal à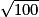 .
.
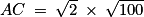
On utilise la propriété suivante : pour tout réel positif a et b :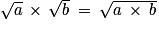
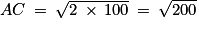
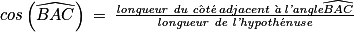
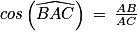
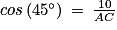
La valeur cos(45°) est une valeur remarquable.
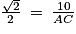
En utilisant la proportionnalité, on a :
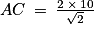
Afin de simplifier la fraction, on peut écrire que 2 est égal à
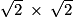
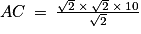
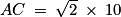
On peut écrire que 10 est égal à
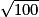 .
.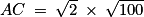
On utilise la propriété suivante : pour tout réel positif a et b :
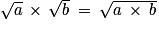
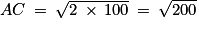
Des rappels sur le théorème de Pythagore peuvent être téléchargés ici.
4.
Lorsqu'une longueur l est agrandie par un rapport k (avec k > 1), alors la nouvelle longueur est égale à l × k.
Lorsqu'une aire A est agrandie par un rapport k (avec k > 1), alors la nouvelle aire est égale à A × k2.
La surface grisée dans le carré initial a pour aire 64 − 16π cm2.
Ainsi, la surface grisée dans le carré sur le sol de la cour aura pour aire (64 − 16π) × 1252 cm2.
Nous avons cependant besoin de convertir cette aire en m2.
On a le tableau suivant :
Donc 1 cm2 = 0,0001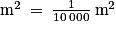 .
.
Ainsi, la surface grisée sur le sol de la cour aura pour aire :
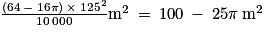
Soit environ 21,46 m2.
De plus, on sait que 1 L de peinture permet de couvrir 7 m2.
On a donc le tableau de proportionnalité suivant :
Ainsi :
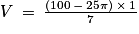
De plus, on utilisera deux couches de peinture. Donc le volume nécessaire sera de :
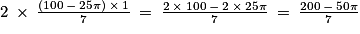
Soit environ 6,13 L.
Or, un pot de peinture contient 750 mL soit 0,75 L de peinture.
En effet, on peut s'aider du tableau de conversion suivant :
Enfin, pour déterminer le nombre de pots, on peut utiliser le tableau de proportionnalité suivant :
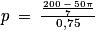
p 8,175
8,175
Or, on va devoir acheter un nombre entier de pots de peinture, on cherche donc le plus petit entier supérieur ou égal à p ; on conseille donc d'acheter 9 pots de peinture.
Lorsqu'une aire A est agrandie par un rapport k (avec k > 1), alors la nouvelle aire est égale à A × k2.
La surface grisée dans le carré initial a pour aire 64 − 16π cm2.
Ainsi, la surface grisée dans le carré sur le sol de la cour aura pour aire (64 − 16π) × 1252 cm2.
Nous avons cependant besoin de convertir cette aire en m2.
On a le tableau suivant :
| m2 | dm2 | cm2 | |||
| | 0 | 0 | 0 | 0 | 1 |
Donc 1 cm2 = 0,0001
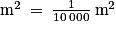 .
.Ainsi, la surface grisée sur le sol de la cour aura pour aire :
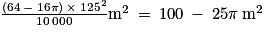
Soit environ 21,46 m2.
De plus, on sait que 1 L de peinture permet de couvrir 7 m2.
On a donc le tableau de proportionnalité suivant :
| Aire (en m2) | 7 | 100 − 25π |
| Volume de peinture (en L) | 1 | V |
Ainsi :
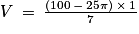
De plus, on utilisera deux couches de peinture. Donc le volume nécessaire sera de :
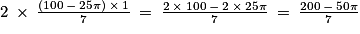
Soit environ 6,13 L.
Or, un pot de peinture contient 750 mL soit 0,75 L de peinture.
En effet, on peut s'aider du tableau de conversion suivant :
| daL | L | dL | cL | mL |
| | 0 | 7 | 5 | 0 |
Enfin, pour déterminer le nombre de pots, on peut utiliser le tableau de proportionnalité suivant :
| Nombre de pots | 1 | p |
| Volume de peinture (en L) | 0,75 | 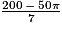 |
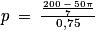
p
 8,175
8,175Or, on va devoir acheter un nombre entier de pots de peinture, on cherche donc le plus petit entier supérieur ou égal à p ; on conseille donc d'acheter 9 pots de peinture.
Exercice 4 (3 points)
1.
55 % des enfants sont des filles : il s'agit d'une proportion. Pour obtenir le nombre de filles on calcule donc :
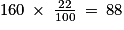
On peut en déduire le nombre de garçons :
160 − 88 = 72
De plus, trois quarts des garçons utilisent les jeux :
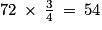
On peut en déduire le nombre de garçons n'utilisant pas les jeux :
72 − 54 = 18
La moitié des filles utilisent les jeux :
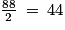
Et donc la moitié n'utilisent pas les jeux, donc 44 filles également.
Enfin, on peut calculer le nombre d'enfants utilisant les jeux :
44 + 54 = 98
Et le nombre d'enfants n'utilisant pas les jeux :
44 + 18 = 62
On peut également vérifier que l'on a bien 98 + 62 = 160.
Voici donc le tableau complété :
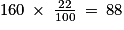
On peut en déduire le nombre de garçons :
160 − 88 = 72
De plus, trois quarts des garçons utilisent les jeux :
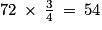
On peut en déduire le nombre de garçons n'utilisant pas les jeux :
72 − 54 = 18
La moitié des filles utilisent les jeux :
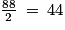
Et donc la moitié n'utilisent pas les jeux, donc 44 filles également.
Enfin, on peut calculer le nombre d'enfants utilisant les jeux :
44 + 54 = 98
Et le nombre d'enfants n'utilisant pas les jeux :
44 + 18 = 62
On peut également vérifier que l'on a bien 98 + 62 = 160.
Voici donc le tableau complété :
| | Filles | Garçons | Total |
| Utilisent | 44 | 54 | 98 |
| N'utilisent pas | 44 | 18 | 62 |
| Total | 88 | 72 | 160 |
2.
La proportion (en pourcentage) d'enfants qui utilisent les jeux est égale à :
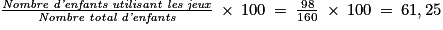
Ainsi, on peut affirmer que 61,25 % des enfants utilisent les jeux.
Attention : ne pas écrire dans le calcul que :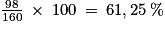 .
.
En effet,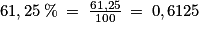 .
.
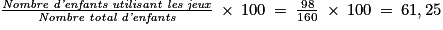
Ainsi, on peut affirmer que 61,25 % des enfants utilisent les jeux.
Attention : ne pas écrire dans le calcul que :
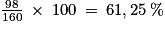 .
. En effet,
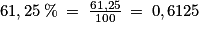 .
.3.
Déterminons la proportion (en pourcentage) de filles parmi les enfants qui utilisent les jeux. Il s'agit d'une fréquence conditionnelle.
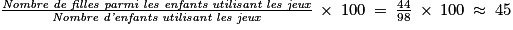
Ainsi, environ 45 % des enfants utilisant les jeux de cour sont des filles.
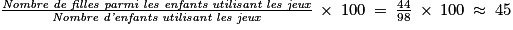
Ainsi, environ 45 % des enfants utilisant les jeux de cour sont des filles.
Des rappels sur les fréquences conditionnelles peuvent être téléchargés sur le site Éduscol.
Exercice 5 (4 points)
QCM
Q1
Q1
En langage algorithmique, on traduit le programme Scratch par :
a ← 4
b ← a + 2
Première ligne : une variable a est créée et la valeur 4 est affectée à la variable a. Donc : a = 4.
Seconde ligne : une variable b est créée et la valeur a+2 est affectée à la variable b. Or, la dernière valeur en mémoire concernant la variable a est 4, donc la valeur affectée à b est 4 + 2. Ainsi b = 6.
La réponse correcte est donc la réponse B.
a ← 4
b ← a + 2
Première ligne : une variable a est créée et la valeur 4 est affectée à la variable a. Donc : a = 4.
Seconde ligne : une variable b est créée et la valeur a+2 est affectée à la variable b. Or, la dernière valeur en mémoire concernant la variable a est 4, donc la valeur affectée à b est 4 + 2. Ainsi b = 6.
La réponse correcte est donc la réponse B.
Q2
Une variable a est créée et la valeur 2 est affectée à a. Donc pour l'instant a = 2.
On va ensuite répéter 4 fois l'action suivante :
a ← a + 3
On peut reformuler cette action par « une nouvelle valeur va être affectée à la variable a : cette nouvelle valeur est son ancienne valeur à laquelle on va ajouter 3 ».
La réponse correcte est donc la réponse C.
On va ensuite répéter 4 fois l'action suivante :
a ← a + 3
On peut reformuler cette action par « une nouvelle valeur va être affectée à la variable a : cette nouvelle valeur est son ancienne valeur à laquelle on va ajouter 3 ».
| Répétition | 1re fois | 2e fois | 3e fois | 4e fois |
| a | 2 + 3 = 5 | 5 + 3 = 8 | 8 + 3 = 11 | 11 + 3 = 14 |
La réponse correcte est donc la réponse C.
Des explications complémentaires sur la répétition en langage Scratch peuvent être téléchargées ici.
Q3
Lorsqu'une longueur l est réduite par un rapport k (avec 0 < k < 1), alors la nouvelle longueur est égale à l × k.
Lorsqu'une aire A est réduite par un rapport k (avec 0 < k < 1), alors la nouvelle aire est égale à A × k2.
Lorsqu'un volume V est réduit par un rapport k (avec 0 < k < 1), alors le nouveau volume est égal à V × k3.
La réponse correcte est donc la réponse A.
Lorsqu'une aire A est réduite par un rapport k (avec 0 < k < 1), alors la nouvelle aire est égale à A × k2.
Lorsqu'un volume V est réduit par un rapport k (avec 0 < k < 1), alors le nouveau volume est égal à V × k3.
La réponse correcte est donc la réponse A.
Q4
Calculons dans un premier temps le volume du réservoir en m3 :
V = l × L × h = 1,5 × 1,5 × 2 = 4,5 m3
De plus, on sait que 1 L = 1 dm3 (cette égalité est à connaître par cœur).
Utilisons maintenant le tableau d'unités suivant :
On a donc :
V = 4500 dm3
Ainsi :
V = 4500 L
La réponse correcte est donc la réponse B.
V = l × L × h = 1,5 × 1,5 × 2 = 4,5 m3
De plus, on sait que 1 L = 1 dm3 (cette égalité est à connaître par cœur).
Utilisons maintenant le tableau d'unités suivant :
| m3 | dm3 | ||||
| | | 4 | 5 | 0 | 0 |
On a donc :
V = 4500 dm3
Ainsi :
V = 4500 L
La réponse correcte est donc la réponse B.
Sujet corrigé réalisé par Jean Delautre, professeur de mathématiques au lycée Notre-Dame de la Paix à Lille.
Document précédent
Sujet zéro, Partie A, Français (nouveau)
