Dernier essai le
- Score :
/20
Sujet
Sujet
L'épreuve est notée sur 20. Une note globale égale ou inférieure à 5 est éliminatoire. Durée de l'épreuve : 3 h ; coefficient 1
Le sujet est composé de 5 exercices indépendants permettant de vérifier les connaissances du candidat.
Corrigé
Corrigé
Exercice 1
Partie A
1.
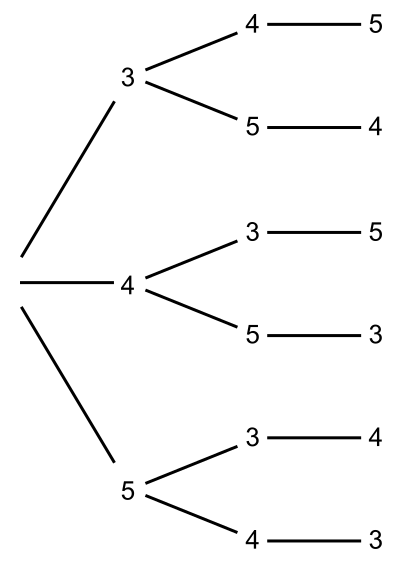
a. Il s'agit d'un tirage sans remise de cartes numérotées de 3 à 5 pour former un nombre entier de trois chiffres : les six résultats équiprobables possibles sont donc :
345 – 354 – 435 – 453 – 534 – 543
Remarque : on peut, si besoin, élaborer un arbre des possibles pour établir la liste exhaustive de tous les résultats.
345 – 354 – 435 – 453 – 534 – 543
Remarque : on peut, si besoin, élaborer un arbre des possibles pour établir la liste exhaustive de tous les résultats.
 |
Pour une notion de probabilités, on pourra visionner la vidéo Introduction aux probabilités, feuilleter Le manuel 3e Sésamath et pour approfondir, consulter les ressources d'accompagnement des anciens programmes sur Eduscol : Probabilités
b. Parmi ces six résultats, deux sont pairs (354 et 534) : la probabilité d'obtenir un nombre pair est donc égale à 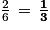 .
.
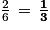 .
.c. Parmi ces six résultats, quatre ne sont pas des multiples de 5 : la probabilité de ne pas obtenir un multiple de 5 est donc égale à 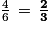 .
.
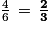 .
.d. Un nombre entier est divisible par 3 si et seulement si la somme des chiffres qui le composent est divisible par 3 ; or, la somme des chiffres des 6 résultats est égale à 3 + 4 + 5 = 12, donc tous les nombres formés sont divisibles par 3. La probabilité d'avoir un nombre divisible par 3 (événement certain) est égale à 1.
2.
a. Il s'agit d'un tirage avec remise de deux cartes parmi trois cartes numérotées de 3 à 5. On obtiendra donc 3 × 3 = 9 résultats équiprobables possibles :
33 – 34 – 35 – 43 – 44 – 45 – 53 – 54 – 55
Si besoin, voici l'arbre des possibles :
33 – 34 – 35 – 43 – 44 – 45 – 53 – 54 – 55
Si besoin, voici l'arbre des possibles :
 |
La probabilité d'obtenir un nombre avec deux chiffres identiques est égale à 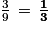 .
.
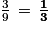 .
.b. Parmi ces 9 résultats, seuls les nombres 45 et 54 sont divisibles par 9.
La probabilité d'obtenir un multiple de 9 est égale à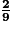 .
.
La probabilité d'obtenir un multiple de 9 est égale à
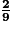 .
.c. Les trois nombres 33, 34 et 35 sont inférieurs à 40, donc la probabilité d'obtenir un nombre inférieur à 40 est égale à 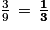 .
.
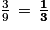 .
.Partie B
1.
On sait que la proportion des boules rouges dans le sac est de 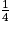 et qu'il y a deux fois moins de boules jaunes que de boules rouges, donc la probabilité que la boule tirée soit jaune est égale à la moitié de
et qu'il y a deux fois moins de boules jaunes que de boules rouges, donc la probabilité que la boule tirée soit jaune est égale à la moitié de 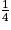 soit
soit 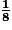 .
.
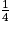 et qu'il y a deux fois moins de boules jaunes que de boules rouges, donc la probabilité que la boule tirée soit jaune est égale à la moitié de
et qu'il y a deux fois moins de boules jaunes que de boules rouges, donc la probabilité que la boule tirée soit jaune est égale à la moitié de 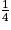 soit
soit 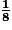 .
.2.
La somme des probabilités des trois événements « tirer une boule bleue », « tirer une boule rouge » et « tirer une boule jaune » étant égale à 1 (événement certain), la probabilité que la boule tirée soit bleue est donc égale à :
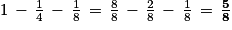 .
.
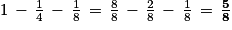 .
.3.
Si n est le nombre total de boules dans le sac, alors puisqu'il y a 7 boules jaunes, 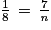 . En effectuant un produit en croix, on obtient 56. Il y a donc 56 boules en tout : 7 jaunes, 14 rouges (le double) et 56 − (14 + 7) = 56 − 21 = 35 boules bleues.
. En effectuant un produit en croix, on obtient 56. Il y a donc 56 boules en tout : 7 jaunes, 14 rouges (le double) et 56 − (14 + 7) = 56 − 21 = 35 boules bleues.
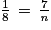 . En effectuant un produit en croix, on obtient 56. Il y a donc 56 boules en tout : 7 jaunes, 14 rouges (le double) et 56 − (14 + 7) = 56 − 21 = 35 boules bleues.
. En effectuant un produit en croix, on obtient 56. Il y a donc 56 boules en tout : 7 jaunes, 14 rouges (le double) et 56 − (14 + 7) = 56 − 21 = 35 boules bleues.Exercice 2
1.
Soit x le nombre de vidéos téléchargées : le coût total en euros est de 0,7 × x avec l'offre F. On en déduit que la fonction f qui, au nombre de vidéos téléchargées, associe le coût en euros avec l'offre F est 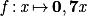 .
.
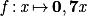 .
.Pour la notion de fonction, on pourra visionner sur Lumni la vidéo Introduction à la notion de fonction, puis pour les fonctions affines et s'entraîner sur les exercices en ligne.
2.
a. Avec l'offre G, les enseignants ont téléchargé 142 vidéos pour un montant de 98,20 €. Comme l'abonnement est de 13 €, ils ont payé 98,20 − 13 = 85,20 € pour les 142 téléchargements, donc le montant fixe par téléchargement est de 85,20 ÷ 142 = 0,60 €.
On en déduit (non demandé) que la fonction g qui, au nombre de vidéos téléchargées, associe le coût en euros avec l'offre G est
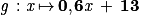 et puisque
et puisque 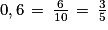 ,
, 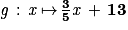 .
.
On en déduit (non demandé) que la fonction g qui, au nombre de vidéos téléchargées, associe le coût en euros avec l'offre G est
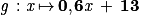 et puisque
et puisque 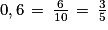 ,
, 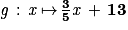 .
.b. 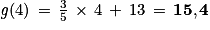
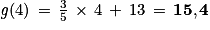
c. g(10) représente le coût total pour le téléchargement de 10 vidéos avec l'offre G.
d. 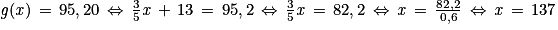 . Cette équipe a téléchargé 137 vidéos avec l'offre G.
. Cette équipe a téléchargé 137 vidéos avec l'offre G.
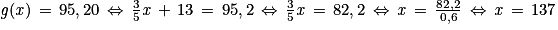 . Cette équipe a téléchargé 137 vidéos avec l'offre G.
. Cette équipe a téléchargé 137 vidéos avec l'offre G.Pour la résolution des équations, on pourra consulter le site Euler - Wims de l'académie de Versailles.
3.
Soit x un nombre de vidéos téléchargées pour lequel l'offre G est plus intéressante que l'offre F, alors :
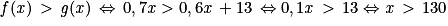
Il faut télécharger au moins 131 vidéos pour que l'offre G soit plus intéressante.
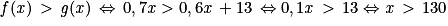
Il faut télécharger au moins 131 vidéos pour que l'offre G soit plus intéressante.
Pour la résolution des inéquations, on pourra se référer au site Euler - Wims de l'académie de Versailles.
4.
Il y a une erreur dans le tableau donné dans l'énoncé : les prix indiqués sur la ligne 2 correspondent au prix payé avec l'offre G et non l'offre F. Voici un tableau correct avec une ligne supplémentaire pour l'offre G :
| Nombre de vidéos téléchargées | 50 | 100 | 150 | 200 | 250 |
| Dépense en € avec l'offre F | 35 | 70 | 105 | 140 | 175 |
| Dépense en € avec l'offre G | 43 | 73 | 103 | 133 | 163 |
| Dépense en € avec l'offre G remisée | 34,40 | 58,40 | 82,40 | 106,40 | 130,40 |
Vous devez savoir utiliser les fonctions habituelles d'un tableur (voir par exemple les exercices sur https://clg-monnet-briis.ac-versailles.fr/Utiliser-un-tableur ou sur le site le site Euler - Wims de l'académie de Versailles, ce qui vous permettra aussi de cerner la notion de variable, comme précisé dans le document « Utiliser le calcul littéral » sur le site Eduscol « L'utilisation du tableur peut faciliter la compréhension de la notion de variable dans la mesure où, dans l'édition d'une formule, ce sont les adresses des cellules (et non leur contenu) qui sont prises en compte. La modification du contenu d'une cellule désignée dans une formule modifie le contenu de la cellule où est implantée la formule, ce qui permet d'appréhender les notions de variable et de fonction. »
a. On a pu saisir comme formule dans la cellule B2 et étirer sur toute la ligne pour obtenir le montant de la dépense avec l'offre F :
= 0,7*B2
= 0,7*B2
b. On a pu saisir comme formule dans la cellule B3 et étirer sur toute la ligne pour obtenir le montant de la dépense avec l'offre G remisée :
= 0,8*(0,6*B2 + 13)
En effet, une remise de 20 % revient à ne payer que 80 % du coût initial.
= 0,8*(0,6*B2 + 13)
En effet, une remise de 20 % revient à ne payer que 80 % du coût initial.
Exercice 3
On rappelle qu'en mathématiques une affirmation est soit vraie, soit fausse (elle n'est jamais parfois vraie !).
Pour justifier qu'une affirmation est fausse, on peut exhiber un contre-exemple (puisque ce n'est pas vrai sur cet exemple, l'affirmation est fausse).
En revanche, un ou de très nombreux exemples ne permettent pas de dire qu'une affirmation est vraie : il faut le démontrer dans le cas général.
Pour justifier qu'une affirmation est fausse, on peut exhiber un contre-exemple (puisque ce n'est pas vrai sur cet exemple, l'affirmation est fausse).
En revanche, un ou de très nombreux exemples ne permettent pas de dire qu'une affirmation est vraie : il faut le démontrer dans le cas général.
1.
L'affirmation 1 est fausse : la fraction 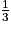 est un contre-exemple. En effet, la partie décimale du quotient de 1 par 3 est infinie (la division ne s'arrête jamais), contrairement aux nombres décimaux qui ont une partie décimale finie.
est un contre-exemple. En effet, la partie décimale du quotient de 1 par 3 est infinie (la division ne s'arrête jamais), contrairement aux nombres décimaux qui ont une partie décimale finie.
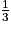 est un contre-exemple. En effet, la partie décimale du quotient de 1 par 3 est infinie (la division ne s'arrête jamais), contrairement aux nombres décimaux qui ont une partie décimale finie.
est un contre-exemple. En effet, la partie décimale du quotient de 1 par 3 est infinie (la division ne s'arrête jamais), contrairement aux nombres décimaux qui ont une partie décimale finie.On retrouvera les définitions des différents types de nombres sur le document ressource Fractions et nombres décimaux au cycle 3 à partir de la page 3.
2.
L'affirmation 2 est vraie : tout entier relatif k (positif ou négatif) est un nombre décimal, puisqu'il peut s'écrire sous la forme d'une fraction décimale :
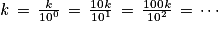
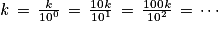
3.
L'affirmation 3 est vraie ; démontrons-le :
Soit k un nombre entier impair, alors le reste de la division euclidienne de k par 2 est égal à 1, donc si q est le quotient entier de k par 2, alors k = 2q + 1.
k2 = (2q + 1)2 = 4q2 + 4q + 1 = 2(2q2 + 2q) + 1
Comme q est un entier,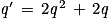 est un entier.
est un entier.
L'égalité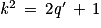 prouve que k2 est impair, puisque le reste de sa division euclidienne par 2 est égal à 1.
prouve que k2 est impair, puisque le reste de sa division euclidienne par 2 est égal à 1.
Soit k un nombre entier impair, alors le reste de la division euclidienne de k par 2 est égal à 1, donc si q est le quotient entier de k par 2, alors k = 2q + 1.
k2 = (2q + 1)2 = 4q2 + 4q + 1 = 2(2q2 + 2q) + 1
Comme q est un entier,
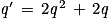 est un entier.
est un entier.L'égalité
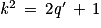 prouve que k2 est impair, puisque le reste de sa division euclidienne par 2 est égal à 1.
prouve que k2 est impair, puisque le reste de sa division euclidienne par 2 est égal à 1.4.
L'affirmation 4 est fausse : considérons comme contre-exemple le produit de 0,2 par 0,5 qui est égal à 0,1 ; or 0,1 < 0,2 et 0,1 < 0,5.
5.
L'affirmation 5 est fausse : considérons comme contre-exemple un prix initial de 100 €. Après une augmentation de 15 %, ce prix monte à :
(1 + 15 %) × 100 = 1,15 × 100 = 115 €
Si on réduit de 15 % ces 115 €, on obtient :
(1 − 15 %) × 115 = 0,85 × 115 = 97,75 €
Remarque : Après une augmentation de 15 %, il faudrait diminuer le prix d'environ 13,04 % pour le ramener à sa valeur initiale.
(1 + 15 %) × 100 = 1,15 × 100 = 115 €
Si on réduit de 15 % ces 115 €, on obtient :
(1 − 15 %) × 115 = 0,85 × 115 = 97,75 €
Remarque : Après une augmentation de 15 %, il faudrait diminuer le prix d'environ 13,04 % pour le ramener à sa valeur initiale.
Exercice 4
Il est nécessaire avant de se présenter au CRPE de s'entraîner à la programmation, si possible avec Scratch (en ligne scratch.mit.edu/download/scratch2) dont vous remarquez dans l'adresse qu'il a été développé par le MIT (pour les enfants).
On pourra consulter le document ressource « Algorithme et programmation » des programmes du cycle 4.
On pourra consulter le document ressource « Algorithme et programmation » des programmes du cycle 4.
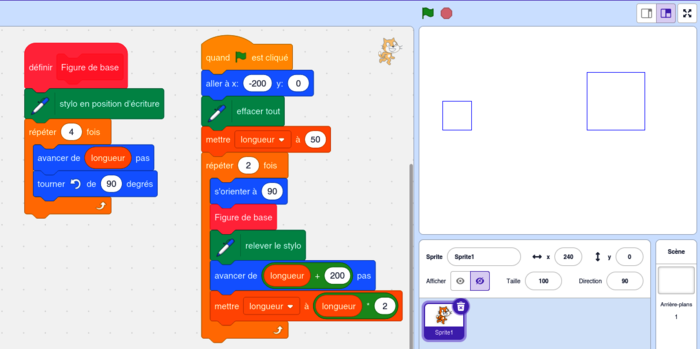
Voici le programme en couleurs, pour mieux voir et vous entraîner sur Scratch :
 |
1.
La figure de base est un carré (quadrilatère de quatre côtés de même longueur et qui possède 4 angles droits).
Explications (non demandées)
Explications (non demandées)
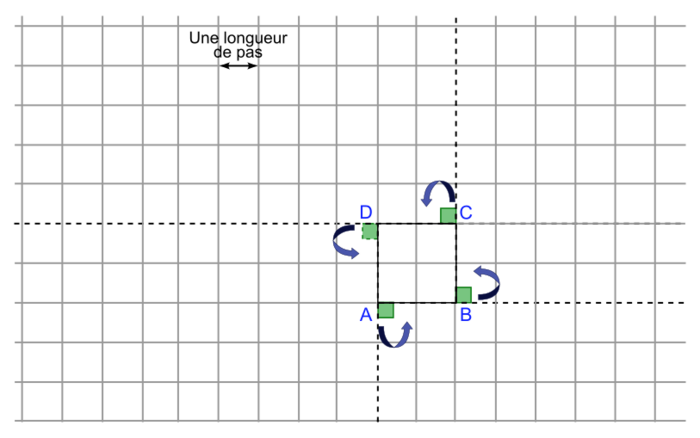 |
Supposons que la longueur d'un côté du quadrillage soit d'une longueur de pas et qu'initialement le curseur soit positionné sur A. S'il est « orienté à 90 » comme c'est le cas dans le programme principal, alors le stylo en position d'écriture va tracer le segment [AB] puis va tourner dans le sens inverse des aiguilles d'une montre de 90°.
Il trace ensuite le segment [BC] puis tourne dans le sens inverse des aiguilles d'une montre de 90° pour tracer [CD]. Il tourne une nouvelle fois dans le sens inverse des aiguilles d'une montre de 90° pour tracer [DA] puis sur le point A, se tourne pour s'orienter sur l'horizontale vers la droite (position de départ).
Il trace ensuite le segment [BC] puis tourne dans le sens inverse des aiguilles d'une montre de 90° pour tracer [CD]. Il tourne une nouvelle fois dans le sens inverse des aiguilles d'une montre de 90° pour tracer [DA] puis sur le point A, se tourne pour s'orienter sur l'horizontale vers la droite (position de départ).
2.
Au début, la variable longueur vaut 50, le premier carré a donc des côtés de longueur 50 pas. Ensuite il avance de 50 pas + 200 pas = 250 pas, pour tracer un carré de longueur 100 pas.
Comme pour construire la figure, on doit prendre 1 mm pour 5 pas ; on construira un premier carré de 10 mm = 1 cm de côté pour 50 pas, on laissera une distance entre les deux carrés de 4 cm (200 pas), puis on construira un carré de 2 cm de côté.
Comme pour construire la figure, on doit prendre 1 mm pour 5 pas ; on construira un premier carré de 10 mm = 1 cm de côté pour 50 pas, on laissera une distance entre les deux carrés de 4 cm (200 pas), puis on construira un carré de 2 cm de côté.
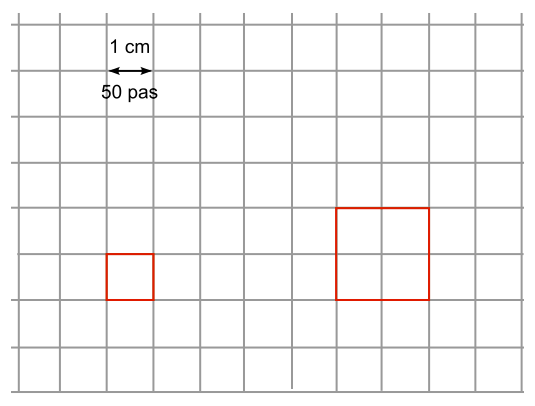 |
3.
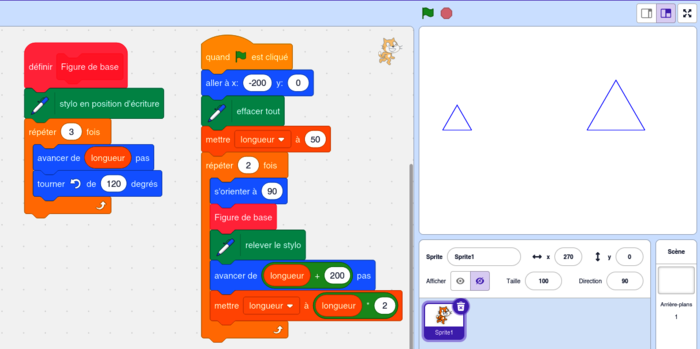 |
a. Dans le bloc « figure de base », on doit demander de répéter 3 fois (et non 4) d'avancer de 50 pas puis de tourner de 120°. En effet, il se positionne au point A, se déplace horizontalement vers la droite pour arriver au point B et doit tourner de 120° pour « remonter » au 3e sommet du triangle équilatéral.
Rappel : les trois angles d'un triangle équilatéral font 60°, mais pour le dessiner, il faut bien à chaque fois effectuer une rotation de 120° (180 – 60 = 120).
Rappel : les trois angles d'un triangle équilatéral font 60°, mais pour le dessiner, il faut bien à chaque fois effectuer une rotation de 120° (180 – 60 = 120).
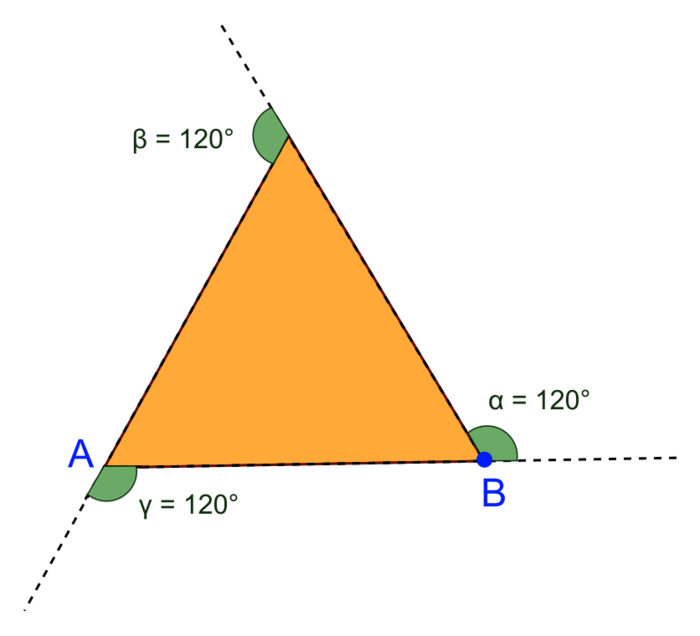 |
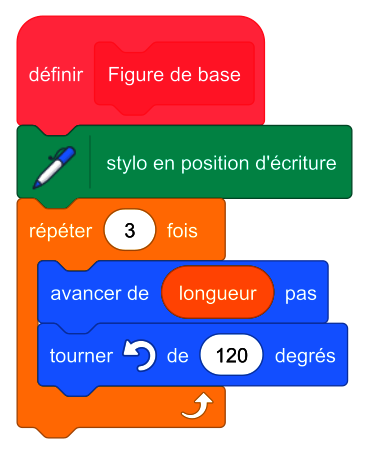 |
b. Le côté du deuxième triangle a une longueur deux fois plus grande que celui du premier triangle : l'aire du deuxième triangle sera donc 22 = 4 fois plus grande que celle du premier triangle (comme on peut le visualiser ci-dessous) :
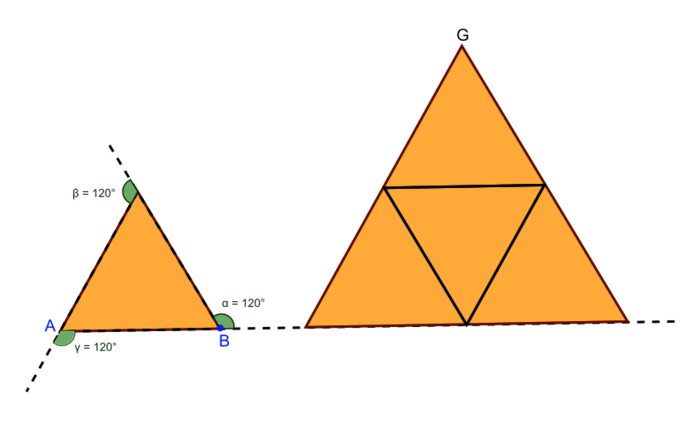 |
Rappel : lors d'un agrandissement (k > 1) ou une réduction (k < 1) de rapport k :
- toutes les longueurs sont multipliées par k,
- toutes les aires sont multipliées par k2,
- tous les volumes sont multipliés par k3.
Exercice 5
1.
Si on choisit − 3 comme nombre de départ :
Avec le programme A :
On l'élève au carré : (− 3)2 = 9
On soustrait son quadruple : 9 − 4 × (−3) = 9 + 12 = 21
Avec le programme A :
On l'élève au carré : (− 3)2 = 9
On soustrait son quadruple : 9 − 4 × (−3) = 9 + 12 = 21
Avec le programme B :
On lui retranche 9 : (−3) − 9 = −12
On lui ajoute 3 : (−3) + 3 = 0
On multiplie ces deux résultats : 12 × 0 = 0
On lui retranche 9 : (−3) − 9 = −12
On lui ajoute 3 : (−3) + 3 = 0
On multiplie ces deux résultats : 12 × 0 = 0
2.
Si on note x le nombre initialement choisi :
Avec le programme B :
On lui retranche 9 : x − 9
On lui ajoute 3 : x + 3
On multiplie ces deux résultats :
(x − 9)(x + 3) = x2 + 3x − 9x − 27 = x2 − 6x − 27
Avec le programme B :
On lui retranche 9 : x − 9
On lui ajoute 3 : x + 3
On multiplie ces deux résultats :
(x − 9)(x + 3) = x2 + 3x − 9x − 27 = x2 − 6x − 27
3.
Si on note x le nombre initialement choisi :
Avec le programme A :
On l'élève au carré : x2
On soustrait son quadruple : x2 −4x
Si on obtient le même résultat avec les deux programmes, alors :
x2 − 6x − 27 = x2 − 4x
On en déduit :
−6x − 27 = −4x
Soit :
−2x = 27
Soit :
x = −13,5
Vérifions :
Si x = −13,5, alors :
On obtient avec le programme A :
x2 − 4x = (−13,5)2 − 4 × (−13,5) = 182,25 − (−54) = 182,25 + 54 = 236,25
On obtient avec le programme B :
(x − 9)(x + 3) = (−13,5 − 9)(−13,5 + 3) = (−22,5) × (−10,5) = 236,25
Avec le programme A :
On l'élève au carré : x2
On soustrait son quadruple : x2 −4x
Si on obtient le même résultat avec les deux programmes, alors :
x2 − 6x − 27 = x2 − 4x
On en déduit :
−6x − 27 = −4x
Soit :
−2x = 27
Soit :
x = −13,5
Vérifions :
Si x = −13,5, alors :
On obtient avec le programme A :
x2 − 4x = (−13,5)2 − 4 × (−13,5) = 182,25 − (−54) = 182,25 + 54 = 236,25
On obtient avec le programme B :
(x − 9)(x + 3) = (−13,5 − 9)(−13,5 + 3) = (−22,5) × (−10,5) = 236,25
Le seul nombre initial qui permet d'obtenir le même résultat avec les deux programmes est −13,5.
On pourra se référer pour les équations au site Euler - Wims de l'académie de Versailles.
Exercice 6
1.
Volume du cône = 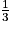 × aire de la base × hauteur.
× aire de la base × hauteur.
Volume du cône =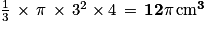 .
.
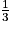 × aire de la base × hauteur.
× aire de la base × hauteur.Volume du cône =
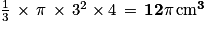 .
.2.
Volume du cylindre = aire de la base × hauteur.
Volume du cylindre = π × 32 × 8 = 72π cm3.
Volume du cylindre = π × 32 × 8 = 72π cm3.
3.
Considérons le triangle 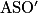 rectangle en
rectangle en 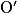 : d'après le théorème de Pythagore,
: d'après le théorème de Pythagore, 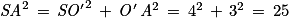 .
.
On en déduit :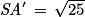 , soit
, soit 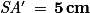 .
.
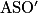 rectangle en
rectangle en 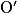 : d'après le théorème de Pythagore,
: d'après le théorème de Pythagore, 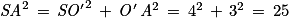 .
.On en déduit :
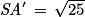 , soit
, soit 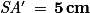 .
.Propriété de Pythagore (permettant de calculer la longueur d'un côté d'un triangle rectangle quand on connaît la longueur de ses deux autres côtés).
Si un triangle est rectangle, alors le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Si un triangle est rectangle, alors le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
4.
Pour la classe de 24 élèves possédant chacun un poudrier rempli de stevia, il faudra donc 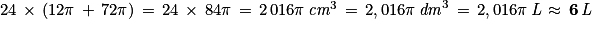 .
.
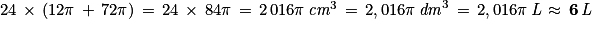 .
.Seules les unités de capacités (L, dL, cL, etc.) sont enseignées à l'école primaire, mais il convient de connaître une de leurs correspondances avec les unités de volume, 1 dm3 = 1 L ou 1 m3 = 1 000 L pour en déduire le tableau ci-dessous :
 |
Attention : 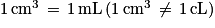 .
.
Le symbole du litre est L en majuscule… depuis 1979.
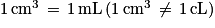 .
.Le symbole du litre est L en majuscule… depuis 1979.
5.
a. La longueur de l'arc de cercle d'extrémités A et 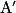 est égale à la longueur d'un cercle de rayon 3 cm = 2 × π × 3 = 6π cm.
est égale à la longueur d'un cercle de rayon 3 cm = 2 × π × 3 = 6π cm.
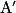 est égale à la longueur d'un cercle de rayon 3 cm = 2 × π × 3 = 6π cm.
est égale à la longueur d'un cercle de rayon 3 cm = 2 × π × 3 = 6π cm.b. On peut compléter ce tableau de proportionnalité avec les réponses des questions précédentes et effectuer un produit en croix.
La mesure de l'angle α est égale à 216°.
Angle au centre en degré qui intercepte l'arc d'extrémités A et 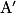 | Longueur de l'arc d'extrémités A et 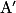 en cm en cm |
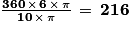 | 6 × π |
| 360 | 2 × π × 5 = 10 × π |
La mesure de l'angle α est égale à 216°.
6. Construisons un patron du saupoudreur à l'échelle 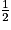 (toutes les longueurs réelles sont divisées par 2, mais pas les angles !).
(toutes les longueurs réelles sont divisées par 2, mais pas les angles !).
La longueur du cercle de rayon 3 cm étant égale à 6π cm interviendra dans le patron pour former la partie cylindrique, soit un rectangle de dimensions réelles 8 cm (hauteur du cylindre) et 6π cm. Dans un patron à l'échelle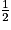 , ce rectangle aura pour dimensions 3π cm soit environ 9,4 cm de longueur et 4 cm de largeur.
, ce rectangle aura pour dimensions 3π cm soit environ 9,4 cm de longueur et 4 cm de largeur.
Interviennent aussi dans le patron à l'échelle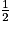 un disque de rayon 1,5 cm correspondant à la base du saupoudreur et un arc de disque de rayon 2,5 cm et d'angle 216° au centre.
un disque de rayon 1,5 cm correspondant à la base du saupoudreur et un arc de disque de rayon 2,5 cm et d'angle 216° au centre.
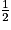 (toutes les longueurs réelles sont divisées par 2, mais pas les angles !).
(toutes les longueurs réelles sont divisées par 2, mais pas les angles !).La longueur du cercle de rayon 3 cm étant égale à 6π cm interviendra dans le patron pour former la partie cylindrique, soit un rectangle de dimensions réelles 8 cm (hauteur du cylindre) et 6π cm. Dans un patron à l'échelle
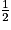 , ce rectangle aura pour dimensions 3π cm soit environ 9,4 cm de longueur et 4 cm de largeur.
, ce rectangle aura pour dimensions 3π cm soit environ 9,4 cm de longueur et 4 cm de largeur.Interviennent aussi dans le patron à l'échelle
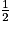 un disque de rayon 1,5 cm correspondant à la base du saupoudreur et un arc de disque de rayon 2,5 cm et d'angle 216° au centre.
un disque de rayon 1,5 cm correspondant à la base du saupoudreur et un arc de disque de rayon 2,5 cm et d'angle 216° au centre.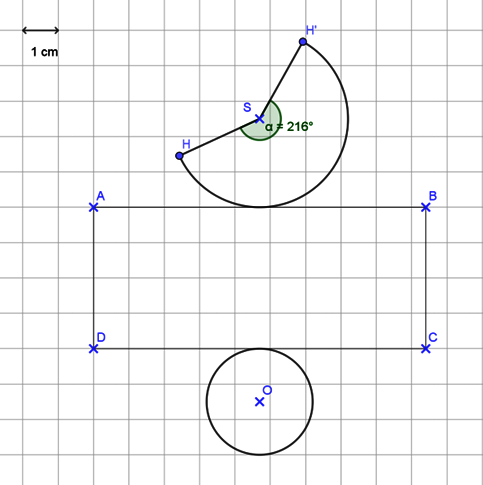 |
Sujet corrigé réalisé par Hélène Radzynski, professeure agrégée de mathématiques, ancienne formatrice de professeurs des écoles en mathématiques.
Document précédent
Sujet 2024 de mathématiques, groupement académique 2
