Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (4 points)
Dans cet exercice, on dira que deux parts sont « égales » lorsqu'elles ont la même aire.
1) On partage un gâteau rectangulaire par ses diagonales. Les parts sont-elles « égales » ? Justifier.
2) On partage un gâteau rectangulaire en traçant trois segments à partir d'un même sommet : un segment vers le sommet opposé et deux segments vers les milieux des côtés opposés (voir figure 1).
 |
Les parts sont-elles « égales » ? Justifier.
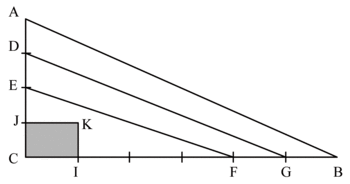
3) ABC est un triangle rectangle en C. [AC] est partagé en quatre segments de même longueur CJ, et [CB] en six segments de même longueur CI. Les polygones EFC, DGFE et ABGD ont-ils la même aire ? Justifier.
On pourra utiliser l'aire du rectangle CIKJ comme unité d'aire.
On pourra utiliser l'aire du rectangle CIKJ comme unité d'aire.
 |
Question complémentaire (4 points)
La question portera sur l'activité « Partager la tarte » décrite dans l'annexe 1.
L'annexe 2 reproduit la feuille de réponse donnée aux élèves.
Les productions de trois élèves se trouvent en annexe 3.
L'annexe 2 reproduit la feuille de réponse donnée aux élèves.
Les productions de trois élèves se trouvent en annexe 3.
1) Indiquer deux compétences en jeu dans cette activité.
2) Pour résoudre ce problème, le maître indique que l'on peut plier une feuille de papier. Citer une autre procédure possible.
3) Expliciter la procédure de pliage utilisée par chaque élève A, B et C ; analyser les justifications données ainsi que les erreurs éventuelles.
4) Quelles activités mathématiques peut-on proposer aux élèves pour prouver la validité de leurs réponses ?
Exercice 2 (4 points)
Vu à la Cité des sciences et de l'industrie à Paris.
« Six réservoirs de formes différentes, de même volume, de même hauteur se remplissent dans le même temps. Il s'agit d'associer à une forme de récipient une jauge et une courbe indiquant la hauteur du liquide en fonction du temps. Les graduations des six jauges A, B, C… indiquent les hauteurs de liquide correspondant à 1 litre, 2 litres… pour les six réservoirs. Les courbes 1, 2, 3… indiquent la hauteur atteinte par le liquide en fonction du temps lorsque les six réservoirs se remplissent. »
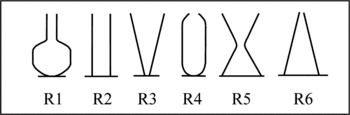 |
Les récipients ont tous le même volume 10 litres et la même hauteur. Leurs formes sont représentées grossièrement par les dessins ci-dessus. Pendant le remplissage, le débit de l'eau est constant et identique d'un récipient à l'autre. Ainsi, à un instant donné, le volume d'eau contenu dans chaque récipient est le même mais la hauteur d'eau n'est pas nécessairement la même.
1) Associer à chaque récipient R1, R2, R3, R4, R5, R6 :
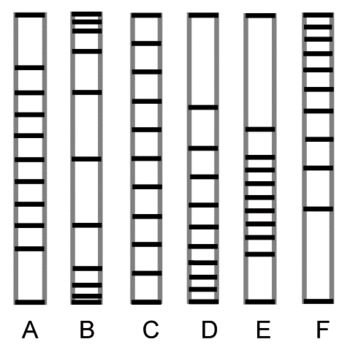
a. la jauge qui lui correspond (parmi les jauges reproduites ci-dessous) ;
 |
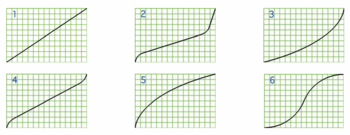
b. la courbe qui lui correspond (parmi les courbes 1, 2, 3, 4, 5, 6 reproduites ci-après).
 |
Présenter les résultats dans un tableau, sans justification.
2) Sachant que le diamètre du récipient cylindrique R2 est de 16 cm, calculer la hauteur de ce récipient (arrondie au centimètre).
3) À un instant t, le récipient cylindrique R2 est rempli aux 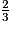 de sa hauteur. Calculer, au dixième de litre près, le volume d'eau V' contenu dans le cylindre à cet instant précis.
de sa hauteur. Calculer, au dixième de litre près, le volume d'eau V' contenu dans le cylindre à cet instant précis.
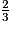 de sa hauteur. Calculer, au dixième de litre près, le volume d'eau V' contenu dans le cylindre à cet instant précis.
de sa hauteur. Calculer, au dixième de litre près, le volume d'eau V' contenu dans le cylindre à cet instant précis.4) On observe la hauteur d'eau dans le récipient R6 au moment où le récipient cylindrique R2 est rempli aux 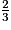 de sa hauteur. Est-elle plus ou moins haute que dans R2 ? Justifier la réponse en utilisant les courbes ci-dessus.
de sa hauteur. Est-elle plus ou moins haute que dans R2 ? Justifier la réponse en utilisant les courbes ci-dessus.
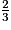 de sa hauteur. Est-elle plus ou moins haute que dans R2 ? Justifier la réponse en utilisant les courbes ci-dessus.
de sa hauteur. Est-elle plus ou moins haute que dans R2 ? Justifier la réponse en utilisant les courbes ci-dessus.Exercice 3 (4 points)
L'objectif de cet exercice est de construire un triangle à partir de ses trois médianes en utilisant les propriétés de la figure.
Les constructions seront effectuées à la règle et au compas : on laissera apparents les traits de construction.
1) Tracer sur la copie deux droites quelconques, d1 et d2, sécantes en un point O.
Placer un point I extérieur à ces deux droites.
Construire le parallélogramme OPQR de centre I tel que P appartienne à d1 et R appartienne à d2. Écrire le programme de construction correspondant.
Placer un point I extérieur à ces deux droites.
Construire le parallélogramme OPQR de centre I tel que P appartienne à d1 et R appartienne à d2. Écrire le programme de construction correspondant.
2) Soit ABC un triangle, G son centre de gravité, M le milieu de [BC] et A' le symétrique de A par rapport à G.
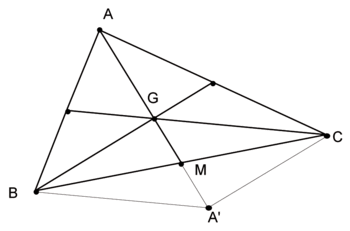 |
a. Montrer que M est le milieu de [GA'].
b. Quelle est la nature du quadrilatère GBA'C ? Justifier.
c. Que peut-on en déduire pour les droites (GB) et (CA') ? Pour les droites (GC) et (BA') ?
3) Tracer sur la copie trois droites quelconques, d1, d2 et d3, sécantes en un point G. Placer sur la droite d1 un point A différent de G.
En utilisant les résultats des questions précédentes, construire le point B sur d2 et le point C sur d3, de sorte que d1, d2 et d3 soient les trois médianes du triangle ABC.
Écrire le programme de construction correspondant.
Écrire le programme de construction correspondant.
Question complémentaire (4 points)
Vous trouverez ci-dessous le descriptif d'une situation extraite de Travaux Géométriques, Apprendre par la résolution de problèmes, cycle 3 (CRDP du Nord-Pas-de-Calais, 2000).
Il s'agit de compléter une figure pour obtenir un rectangle ABCD de centre O (on considère implicitement que M est le milieu de [AB], Q le milieu de [AD] et que AQOM est un rectangle).
Deux mises en œuvre ont été réalisées dans deux CM2 différents.
Il s'agit de compléter une figure pour obtenir un rectangle ABCD de centre O (on considère implicitement que M est le milieu de [AB], Q le milieu de [AD] et que AQOM est un rectangle).
Deux mises en œuvre ont été réalisées dans deux CM2 différents.
Consigne 1 pour la première mise en œuvre :
Complète la figure ci-dessous pour obtenir un rectangle de centre O.
Tu ne peux utiliser que la règle non graduée et le compas.
Complète la figure ci-dessous pour obtenir un rectangle de centre O.
Tu ne peux utiliser que la règle non graduée et le compas.
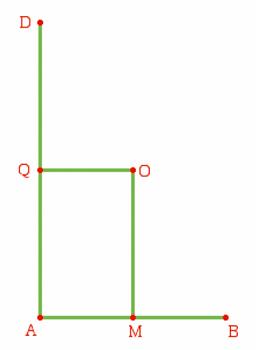 |
Consigne 2 pour la seconde mise en œuvre :
Complète la figure ci-dessous pour obtenir un rectangle de centre O.
Tu ne peux utiliser que la règle graduée.
Complète la figure ci-dessous pour obtenir un rectangle de centre O.
Tu ne peux utiliser que la règle graduée.
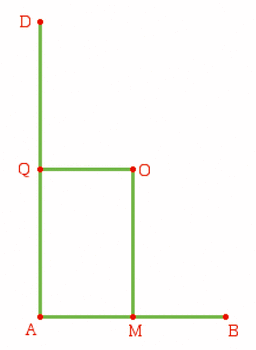 |
1) Pour la consigne 1, citer trois procédures envisageables en CM2 et mentionner pour chacune les propriétés géométriques en jeu.
2) Toujours pour la consigne 1, donner deux types de difficulté que peut rencontrer un élève face à cette tâche.
3) Pour la consigne 2, l'enseignant dispose du document suivant qui présente une procédure particulière.
Extrait du document pour l'enseignant :
« Pour réussir la tâche demandée, il suffit :
- d'utiliser la propriété selon laquelle les diagonales du rectangle ont la même longueur,
- de mesurer la diagonale [BD] (tracée ou non),
- de reporter cette longueur en prolongeant le segment [AO] pour marquer le point C,
- de tracer le rectangle ABCD.
a. La procédure présentée dans ce document est-elle envisageable avec la consigne 1 ? Justifier.
b. Parmi les procédures que vous avez citées pour la consigne 1, certaines peuvent-elles dans leur principe s'appliquer avec la consigne 2 ? Justifier.
4) Proposer un autre instrument géométrique dont l'utilisation amènerait à mettre en œuvre d'autres propriétés du rectangle. Justifier.
Annexes
Annexe 1
Un maître de CM1 propose l'activité suivante :
Voici un partage d'une tarte en quatre parts égales.
 |
Les quatre parts ont la même quantité de croûte (la croûte désigne ici les bords) et la même quantité de garniture. Mais dans la tarte, certains aiment la croûte, et d'autres la garniture.
Trouve une façon de partager la tarte en quatre parts égales :
- pour que les amateurs de croûte aient beaucoup de croûte ;
- pour que les amateurs de garniture aient peu de croûte.
Voilà des feuilles A5 que tu pourras plier pour t'aider à trouver des parts égales.
Annexe 2
Feuille de réponse donnée aux élèves :
Partager la tarte
Dans la tarte, certains aiment la croûte, d'autres la garniture.
Trouve une façon de partager la tarte en quatre parts égales :
Dans la tarte, certains aiment la croûte, d'autres la garniture.
Trouve une façon de partager la tarte en quatre parts égales :
- pour que les amateurs de croûte aient beaucoup de croûte ;
- pour que les amateurs de garniture aient peu de croûte.
1) Explique pourquoi ton partage est bien équitable.
2) As-tu réussi à donner des quantités différentes de croûte à chaque part ? Pourquoi ?
Annexe 3
Travaux d'élèves
Les feuilles de partage reproduites ci-dessous ont été réduites du format A5.
Les feuilles de partage reproduites ci-dessous ont été réduites du format A5.
 |
 |
 |
Corrigé
Corrigé
Exercice 1 (4 points)
1) Les parts du gâteaux sont « égales ». En effet, les triangles générés par les diagonales sont de deux sortes, ceux dont la base est constituée par la longueur du rectangle et la hauteur par sa demi-largeur et ceux dont la base est constituée par la largeur du rectangle et la hauteur par sa demi-longueur. Les autres côtés des triangles sont égaux d'après les propriétés des diagonales du rectangle.
Cette dernière remarque est superflue, puisque pour calculer l'aire d'un triangle, on applique la formule suivante :
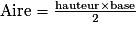 ,
,
soit d'une part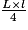 et d'autre part
et d'autre part 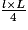 .
.
Cette dernière remarque est superflue, puisque pour calculer l'aire d'un triangle, on applique la formule suivante :
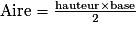 ,
,soit d'une part
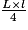 et d'autre part
et d'autre part 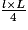 .
.On peut aussi considérer le tracé suivant :
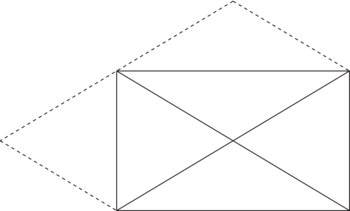 |
Si on considère les parallélogrammes formés à partir des triangles à comparer, on se rend compte que l'aire de chaque triangle correspond à la moitié de l'aire des parallélogrammes. Or cette dernière, la même pour tous, est égale au carré de la moitié de la diagonale.
2) Appelons A1, A2, A3, A4 les aires des 4 triangles générés par les segments cités. L la longueur du rectangle et l sa largeur.
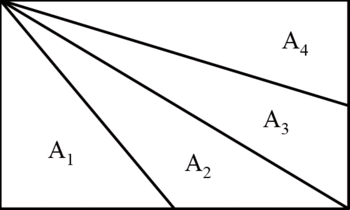 |
Pour les triangles 1 et 2, les hauteurs sont confondues avec la largeur du rectangle, pour les triangles 3 et 4 la hauteur est confondue avec sa longueur.
Utilisons la formule de calcul d'aire des triangles :
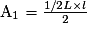 ,
,
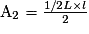 ,
,
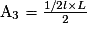 ,
,
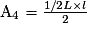 .
.
Ces quatre formules sont équivalentes. Les quatre aires sont égales.
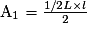 ,
,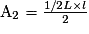 ,
,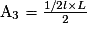 ,
,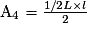 .
.Ces quatre formules sont équivalentes. Les quatre aires sont égales.
3)
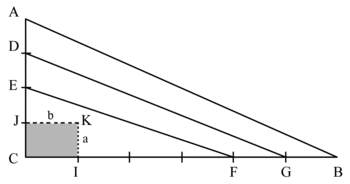 |
Considérons que CJ = JE = ED = DA = a et que CI = FG = GB = b.
L'aire du rectangle CIJK, utilisée comme unité, sera donc ab.
L'aire du rectangle CIJK, utilisée comme unité, sera donc ab.
Cherchons les aires des polygones EFC, DGFE et ABGD.
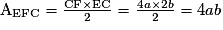 ou 4 fois l'unité d'aire de CIJK.
ou 4 fois l'unité d'aire de CIJK.
ADGFE = ADGC − AEFC
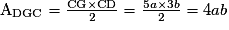
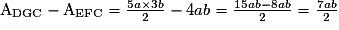 .
.
AABGD = AABC − ADGC
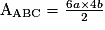
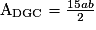
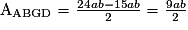 .
.
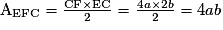 ou 4 fois l'unité d'aire de CIJK.
ou 4 fois l'unité d'aire de CIJK.ADGFE = ADGC − AEFC
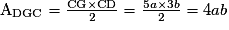
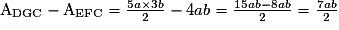 .
.AABGD = AABC − ADGC
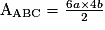
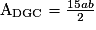
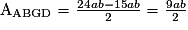 .
.Les polygones EFC, DGFE et ABGD n'ont pas la même aire, puisqu'ils ont respectivement pour aire 4ab, 7ab et 9ab. En revanche, leur somme correspond bien à l'aire du triangle ABC.
Question complémentaire (4 points)
1) Les deux compétences requises par les programmes sont les suivantes :
- classer et ranger des surfaces (figures) selon leur aire (par superposition, découpage et recollement ou pavage par une surface de référence) ;
- construire une surface qui a la même aire qu'une surface donnée (et qui ne lui est pas superposable).
2) On pouvait aussi mesurer à l'aide d'une règle les différentes longueurs. Si on pensait à suivre les diagonales (donnant la largeur de croûte à deux convives et la longueur aux deux autres, comme l'exercice 1 pouvait le laisser suggérer), il était juste nécessaire de savoir les tracer. On pouvait aussi penser à la solution de l'exercice 2, qui garantissait des parts égales avec diverses proportions de croûte et de garniture, et il n'était pas précisé que cette proportion devait être égale. Ceci étant, la solution de l'élève B est la plus judicieuse.
3)
La procédure de pliage est expliquée par l'élève lui-même, un pliage en 8 parts égales (en pliant une fois en deux sur l'axe de symétrie parallèle à la longueur, puis deux fois en deux perpendiculairement). Les parts sont alors regroupées par deux, ainsi qu'il est mentionné, en tenant compte du fait qu'il n'y a pas de croûte entre les parts 2 et 3.
La justification de l'élève concernant l'équité relève davantage de l'énonciation de procédure ; concernant la distribution de croûte, il s'agit d'une observation a posteriori.
L'explication du pliage est peut-être peu mathématique dans sa formulation, mais elle est claire et juste. De même que pour l'élève A, la justification de l'équité, comme celle de la distribution spécifique, relève d'une observation a posteriori. On pouvait attendre une justification portant sur les mesures des côtés d'un rectangle, par exemple, ou sur le fait que plier en suivant un axe de symétrie garantit l'égalité des surfaces.
Élève A
Les amateurs de croûte se retrouvent avec une largeur et une demi-longueur, les autres avec une demi-longueur seulement. La procédure de pliage est expliquée par l'élève lui-même, un pliage en 8 parts égales (en pliant une fois en deux sur l'axe de symétrie parallèle à la longueur, puis deux fois en deux perpendiculairement). Les parts sont alors regroupées par deux, ainsi qu'il est mentionné, en tenant compte du fait qu'il n'y a pas de croûte entre les parts 2 et 3.
La justification de l'élève concernant l'équité relève davantage de l'énonciation de procédure ; concernant la distribution de croûte, il s'agit d'une observation a posteriori.
Élève B
Les amateurs de croûte se retrouvent avec une longueur et une demi-largeur, les autres avec une demi-largeur. C'est la technique la plus efficace.L'explication du pliage est peut-être peu mathématique dans sa formulation, mais elle est claire et juste. De même que pour l'élève A, la justification de l'équité, comme celle de la distribution spécifique, relève d'une observation a posteriori. On pouvait attendre une justification portant sur les mesures des côtés d'un rectangle, par exemple, ou sur le fait que plier en suivant un axe de symétrie garantit l'égalité des surfaces.
Élève C
Les convives reçoivent une quantité de tarte et de croûte différente. Si les convives 1 et 2 reçoivent bien la même part, avec, comme il est indiqué, plus de croûte pour le convive 1, les deux autres sont moins équitablement servis, le convive 3 étant privilégié au détriment de l'autre. Il est probable que l'élève a tenté de plier en deux suivant une diagonale, mais suivant celle d'un carré (dont le côté est la largeur de la tarte) et non suivant celle du rectangle qu'il a travaillé. Cela peut être dû à plusieurs raisons : manipulations habituelles, tentative de répartir croûte et garniture autrement, etc. Comme pour les deux autres élèves, la justification s'avère être une observation.4) On peut suggérer aux élèves, afin de valider leurs propositions, de calculer l'aire de chaque part, à partir d'une unité par exemple (c'est même possible pour le dernier en découpant et repositionnant l'unité), puis de calculer la part de croûte à partir du périmètre du rectangle.
Exercice 2 (4 points)
1)
a. et b.
| Récipients | R1 | R2 | R3 | R4 | R5 | R6 |
| Jauges | E | C | F | A | B | D |
| Courbes | 2 | 1 | 5 | 4 | 6 | 3 |
2) La formule pour trouver le volume d'un cylindre est :
Π r2 × h = V
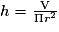
Nous connaissons le volume total, soit 10 litres, c'est-à-dire 10 000 cm3 (1 m3 = 1 000 litres).
Si le diamètre du tube est égal à 16 cm, son rayon est égal à 8 cm.
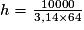
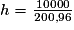
Si on arrondit au centimètre, on obtient une hauteur de 50 cm.
Π r2 × h = V
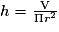
Nous connaissons le volume total, soit 10 litres, c'est-à-dire 10 000 cm3 (1 m3 = 1 000 litres).
Si le diamètre du tube est égal à 16 cm, son rayon est égal à 8 cm.
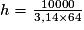
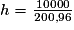
Si on arrondit au centimètre, on obtient une hauteur de 50 cm.
3) On peut procéder de deux manières : soit on calcule le volume d'eau V' lorsque le liquide atteint les deux tiers de 50 cm, soit on calcule les deux tiers du volume total possible.
La deuxième solution est la plus simple et la moins risquée, puisqu'elle part des données de départ et n'est pas assujettie à l'incertitude de Π ni à celle de la hauteur du cylindre, qui était arrondie. De plus, il n'y a pas de problème de conversion.
10 ×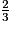 = 6,61.
= 6,61.
La deuxième solution est la plus simple et la moins risquée, puisqu'elle part des données de départ et n'est pas assujettie à l'incertitude de Π ni à celle de la hauteur du cylindre, qui était arrondie. De plus, il n'y a pas de problème de conversion.
10 ×
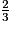 = 6,61.
= 6,61.4) Considérons les courbes 1 (correspondant à R2) et 3 (correspondant à R6) à l'instant t. Sur la courbe 1, repérons l'abscisse correspondant au volume 6,6 litres. Il s'agit de la dixième graduation. Considérons alors quel est le volume atteint au même instant, soit à la même abscisse sur la courbe 3. On trouve un volume de 4 litres. La hauteur d'eau est donc moins importante à l'instant t dans le récipient R6.
Exercice 3 (4 points)
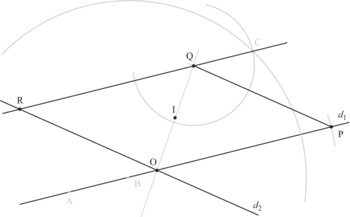
1) Programme
Tracer deux droites quelconques d1 et d2 sécantes en un point O.
Placer un point I extérieur à d1 et d2. Tracer la droite (OI) et chercher sur cette droite le point Q tel que OI = OQ.
OQ est la première diagonale du parallélogramme OPQR.
À l'aide de la règle et du compas, tracer une parallèle à d1 passant par Q. Pour cela, repérer deux points quelconques A et B sur d1. Tracer un cercle de rayon AB et de centre Q. Puis tracer un cercle de rayon AQ et de centre B. À l'intersection de ces cercles se trouve le point C tel que (QC) est parallèle à d1.
Cette parallèle coupe d2 en un point R. Ensuite, il suffit d'utiliser les propriétés du parallélogramme et de chercher le point P, sur d1, tel que OP = QR.
Tracer deux droites quelconques d1 et d2 sécantes en un point O.
Placer un point I extérieur à d1 et d2. Tracer la droite (OI) et chercher sur cette droite le point Q tel que OI = OQ.
OQ est la première diagonale du parallélogramme OPQR.
À l'aide de la règle et du compas, tracer une parallèle à d1 passant par Q. Pour cela, repérer deux points quelconques A et B sur d1. Tracer un cercle de rayon AB et de centre Q. Puis tracer un cercle de rayon AQ et de centre B. À l'intersection de ces cercles se trouve le point C tel que (QC) est parallèle à d1.
Cette parallèle coupe d2 en un point R. Ensuite, il suffit d'utiliser les propriétés du parallélogramme et de chercher le point P, sur d1, tel que OP = QR.
 |
2) a. Le centre de gravité d'un triangle est le point commun aux trois médianes d'un triangle.
Il se trouve aux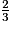 de la longueur de chaque médiane à partir du sommet correspondant, et au
de la longueur de chaque médiane à partir du sommet correspondant, et au 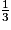 de la longueur de chaque médiane à partir du milieu du côté opposé à ce sommet.
de la longueur de chaque médiane à partir du milieu du côté opposé à ce sommet.
Dans notre triangle, on a :
GA = GA' puisque A' est le symétrique de A par rapport à G.
Par ailleurs :
GM + MA' = GA'
GM + MA' = GA
GM =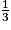 AM
AM
GA =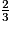 AM
AM
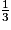 AM + MA' =
AM + MA' = 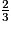 AM
AM
MA' =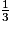 AM
AM
MA' = GM
Il se trouve aux
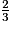 de la longueur de chaque médiane à partir du sommet correspondant, et au
de la longueur de chaque médiane à partir du sommet correspondant, et au 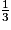 de la longueur de chaque médiane à partir du milieu du côté opposé à ce sommet.
de la longueur de chaque médiane à partir du milieu du côté opposé à ce sommet.Dans notre triangle, on a :
GA = GA' puisque A' est le symétrique de A par rapport à G.
Par ailleurs :
GM + MA' = GA'
GM + MA' = GA
GM =
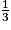 AM
AMGA =
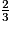 AM
AM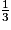 AM + MA' =
AM + MA' = 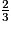 AM
AMMA' =
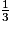 AM
AMMA' = GM
b. Il s'agit d'un parallélogramme quelconque, les diagonales se coupant en leur milieu. GM = MA' et BM = MC.
c. On peut déduire que les droites (GB) et (CA) sont parallèles et isométriques et que les droites (GC) et (BA') sont parallèles et isométriques.
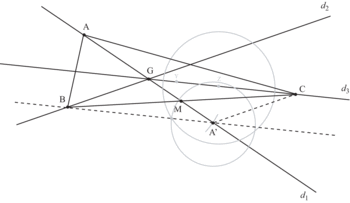
3) Traçons trois droites quelconques d1, d2 et d3 sécantes en G. Plaçons A sur d1. Plaçons M, sur la droite (AG), de manière à ce que GM = 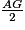 . AM sera alors une médiane du triangle ABC. M devra donc se trouver sur BC, en son milieu.
. AM sera alors une médiane du triangle ABC. M devra donc se trouver sur BC, en son milieu.
Si l'on prend en compte les résultats précédents, que l'on marque le point A', symétrique de A part rapport à G, les points B et C se trouveront sur d2 et d3 de telle manière que (GB) et (A'C) seront symétriques et isométriques.
Comme pour l'exercice 1, il suffira alors, lorsque l'on aura marqué A', de tracer la parallèle à d3 passant par A', de la prolonger jusqu'à ce qu'elle coupe d2 pour obtenir le point B. Par report de mesure, on trouvera alors C sur la droite d2.
Il restera à vérifier que M est bien milieu de BC.
 . AM sera alors une médiane du triangle ABC. M devra donc se trouver sur BC, en son milieu.
. AM sera alors une médiane du triangle ABC. M devra donc se trouver sur BC, en son milieu.Si l'on prend en compte les résultats précédents, que l'on marque le point A', symétrique de A part rapport à G, les points B et C se trouveront sur d2 et d3 de telle manière que (GB) et (A'C) seront symétriques et isométriques.
Comme pour l'exercice 1, il suffira alors, lorsque l'on aura marqué A', de tracer la parallèle à d3 passant par A', de la prolonger jusqu'à ce qu'elle coupe d2 pour obtenir le point B. Par report de mesure, on trouvera alors C sur la droite d2.
Il restera à vérifier que M est bien milieu de BC.
 |
Question complémentaire (4 points)
1)
Repérer à l'aide du compas la mesure de la largeur AB, et décrire un arc de cercle de centre D et de rayon AB. Repérer le point où se coupent les deux arcs de cercle. Relier D puis B à ce point.
Repérer à l'aide du compas la mesure de la longueur AD, et décrire un arc de cercle de centre B et de rayon AD. Repérer le point où se coupent les deux arcs de cercle. Relier D puis B à ce point.
Tracer la droite portée par la deuxième diagonale passant par O. Elle coupera la droite (BQ) en un point C. Relier alors D et C.
Première procédure
Repérer à l'aide du compas la mesure de la largeur AB, et décrire un arc de cercle de centre D et de rayon AB. Refaire la même chose avec la longueur AD, décrire un arc de cercle de centre B et de rayon AD. Repérer le point où se coupent les deux arcs de cercle. Relier D puis B à ce point.Deuxième procédure
Repérer la mesure de la diagonale BD. Tracer un arc de cercle de centre A et de rayon BD.Repérer à l'aide du compas la mesure de la largeur AB, et décrire un arc de cercle de centre D et de rayon AB. Repérer le point où se coupent les deux arcs de cercle. Relier D puis B à ce point.
Deuxième procédure (bis)
Repérer la mesure de la diagonale BD. Tracer un arc de cercle de centre A et de rayon BD. Repérer à l'aide du compas la mesure de la longueur AD, et décrire un arc de cercle de centre B et de rayon AD. Repérer le point où se coupent les deux arcs de cercle. Relier D puis B à ce point.
Troisième procédure
Prolonger le segment QO. Repérer la mesure QO et la reporter sur ce segment. Marquer le point Q' tel que QO = OQ'. On obtient l'axe de symétrie parallèle à la largeur du rectangle. Tracer le segment qui passe par B et Q'.Tracer la droite portée par la deuxième diagonale passant par O. Elle coupera la droite (BQ) en un point C. Relier alors D et C.
2)
Première difficulté
L'élève peut avoir des difficultés à reporter plusieurs mesures différentes. Il faut alors ouvrir son compas en repérant plusieurs longueurs, et planter sa pointe en plusieurs points. La démarche est simple, mais un peu longue.Deuxième difficulté
Il s'agit de repérer des isométries dans la figure (isométrie des diagonales, des longueurs, des axes de symétrie, etc.). Par ailleurs, il faut connaître certaines propriétés, comme celle du milieu des diagonales. Certaines propriétés ou isométries sont observables, d'autres nécessitent une étude préalable.3) a. La procédure présentée est envisageable pour peu que l'on ait reporté soit la longueur, soit la largeur du rectangle à partir des sommets D ou B à l'aide du compas. C'est plus facile avec la règle graduée, mais le principe est bien celui évoqué lors des procédures 2 et 2 bis.
b. La première procédure ne nécessite pas d'utiliser l'isométrie des diagonales puisque c'est sur la largeur et la longueur du rectangle que portent les démarches.
La deuxième procédure applique le même principe, comme nous l'avons vu à la question précédente.
La troisième procédure peut aussi utiliser ce principe de l'isométrie des diagonales, à coupler avec la mesure de l'axe de symétrie.
La deuxième procédure applique le même principe, comme nous l'avons vu à la question précédente.
La troisième procédure peut aussi utiliser ce principe de l'isométrie des diagonales, à coupler avec la mesure de l'axe de symétrie.
4) L'équerre permettrait de répondre aux questions en mettant en évidence les angles droits du rectangle. Il suffirait par exemple de tracer la perpendiculaire à AD passant par D, la perpendiculaire à AB passant par B, et de relier le point d'intersection de ces deux droites.
