Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (5 points)
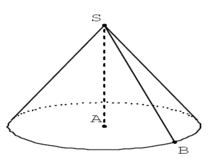 |
Une bougie a la forme d'un cône de révolution de sommet S.
Sa base est un disque de centre A et de rayon 14 cm.
On donne SB = 21 cm.
Sa base est un disque de centre A et de rayon 14 cm.
On donne SB = 21 cm.
1.
On rappelle la formule permettant de calculer le volume V d'un cône :
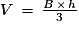 , où B désigne l'aire de la base du cône et h la hauteur du cône.
, où B désigne l'aire de la base du cône et h la hauteur du cône.
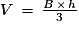 , où B désigne l'aire de la base du cône et h la hauteur du cône.
, où B désigne l'aire de la base du cône et h la hauteur du cône.a) Calculer la valeur exacte de la hauteur de la bougie. En donner une valeur approchée au mm près.
b) Calculer en cm3 le volume exact de la bougie et en donner une valeur approchée au mm3 près.
c) Combien de bougies de ce type peut-on fabriquer avec 20 litres de cire ?
2.
Pour fabriquer ces bougies, on construit un moule en papier qui est un cône de mêmes dimensions que les bougies. La figure ci-dessous représente un patron de ce moule (la figure n'est pas à l'échelle).
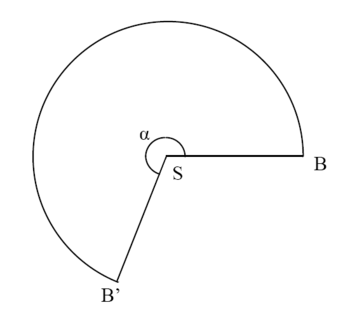 |
a) Calculer la longueur exacte de l'arc de cercle BB'.
b) Calculer l'angle α, en degré.
3. En utilisant le même moule en papier, on décide de fabriquer des bougies bicolores rouges et blanches. On procède de la manière suivante :
- on remplit le moule (pointe en bas) de cire blanche jusqu'à mi-hauteur,
- on complète avec de la cire rouge.
Exercice 2 (3 points)
On se propose de calculer A = 50 000 006 × 70 000 008.
1. En tapant ce produit sur une calculatrice scientifique, on peut voir apparaître sur l'écran :
| 3,50000082 × 1015 |
Justifier, sans calculer A, que cette valeur affichée n'est pas la valeur exacte de A.
2. Toujours sans calculer A, démontrer que 35 × 1014 < A < 48 × 1014. En déduire le nombre de chiffres de A.
3. Le nombre A peut aussi s'écrire (5 × 107 + 6) × (7 × 107 + 8). En utilisant les produits 5 × 7, 5 × 8, 6 × 7 et 6 × 8, déterminer la valeur exacte de A.
4. Soit B = 48 506 557 × 505 149. Calculer en utilisant une calculatrice : 48 506 × 505 ; 557 × 505 ; 48 506 × 149 ; 557 × 149. En déduire, sans nouvelle utilisation de la calculatrice, en écrivant les calculs, la valeur exacte de B.
Question complémentaire (4 points)
Cette question complémentaire s'appuie sur des documents extraits du manuel de l'élève et du livre du maître Euromaths CE1 (Peltier & al., Hatier, 2004).
Annexe 1 : un extrait du manuel de l'élève correspondant au début de la « leçon 54 », page 88.
Annexe 2 : un extrait du livre du maître correspondant à la « leçon 54 », pages 124 et 125.
Annexe 3 : la feuille de calcul utilisée lors de l'activité préparatoire de la « leçon 54 » (fiche photocopiable page 255).
Annexe 1 : un extrait du manuel de l'élève correspondant au début de la « leçon 54 », page 88.
Annexe 2 : un extrait du livre du maître correspondant à la « leçon 54 », pages 124 et 125.
Annexe 3 : la feuille de calcul utilisée lors de l'activité préparatoire de la « leçon 54 » (fiche photocopiable page 255).
La « leçon 54 » du manuel de l'élève est située en fin de période 3, la progression du livre étant prévue sur 5 périodes.
Le signe « × » a été introduit à la fin de la « leçon 53 » pour coder de façon économique des additions réitérées.
En amont, deux « leçons » ont été consacrées à l'utilisation de la calculatrice :
Le signe « × » a été introduit à la fin de la « leçon 53 » pour coder de façon économique des additions réitérées.
En amont, deux « leçons » ont été consacrées à l'utilisation de la calculatrice :
- l'une en période 2 / Objectifs annoncés : « Se familiariser avec la calculatrice – Résoudre des problèmes additifs et soustractifs liés à la numération » ;
- l'autre en début de période 3 / Objectif annoncé : « Utiliser les acquis de la numération pour répondre à des contraintes de calculs ».
1.
On s'intéresse au « jeu du Supercalculateur » proposé lors de l'activité préparatoire décrite dans le livre du maître puis dans l'application présentée dans le manuel de l'élève.
a) Donner les deux procédures mobilisables par les élèves et attendues par le maître dans ce jeu. Pour chacune de ces procédures, indiquer une difficulté et un avantage qu'apporte l'utilisation de la calculatrice.
b) En quoi le fait d'imposer l'utilisation d'une calculatrice dans la règle du jeu semble pertinent pour atteindre l'objectif : « comprendre l'intérêt de transformer une addition réitérée en une multiplication » ?
2. On s'intéresse aux deux premiers calculs de l'exercice 1 de la page 88 (en bas de l'annexe 1). Donner pour chacun une procédure de calcul possible n'utilisant pas la calculatrice et préciser les connaissances qu'elle met en jeu.
3. Un peu plus tard dans la « leçon », le maître choisit de proposer l'exercice suivant :
Au CP, il y a 21 élèves. La maîtresse donne 3 cahiers à chaque élève. Combien de cahiers a-t-elle donnés ?
Donner quatre écritures symboliques que le maître peut accepter comme réponses valides. Expliquer comment elles peuvent être obtenues à partir de la situation décrite (vous pourrez présenter vos réponses dans un tableau).
Au CP, il y a 21 élèves. La maîtresse donne 3 cahiers à chaque élève. Combien de cahiers a-t-elle donnés ?
Donner quatre écritures symboliques que le maître peut accepter comme réponses valides. Expliquer comment elles peuvent être obtenues à partir de la situation décrite (vous pourrez présenter vos réponses dans un tableau).
Exercice 3 (4 points)
1. Parmi les nombres rationnels suivants, quels sont ceux qui sont décimaux ?
Justifier la réponse.
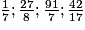
Justifier la réponse.
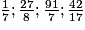
2.
a) Le but de cette question est d'étudier l'écriture décimale périodique de 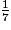 .
.
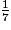 .
.b) Donner, en justifiant succinctement, la 32e décimale du développement périodique de 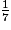 .
.
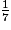 .
.3.
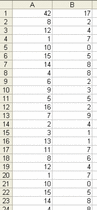 |
Le but de cette question est de produire l'écriture décimale périodique de 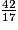 . En utilisant un tableur pour effectuer la division de 42 par 17, on obtient le tableau suivant. À partir de la cellule A2, la colonne A donne les restes successifs de la division de 42 par 17. À partir de la cellule B2, la colonne B donne les quotients successifs.
. En utilisant un tableur pour effectuer la division de 42 par 17, on obtient le tableau suivant. À partir de la cellule A2, la colonne A donne les restes successifs de la division de 42 par 17. À partir de la cellule B2, la colonne B donne les quotients successifs.
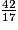 . En utilisant un tableur pour effectuer la division de 42 par 17, on obtient le tableau suivant. À partir de la cellule A2, la colonne A donne les restes successifs de la division de 42 par 17. À partir de la cellule B2, la colonne B donne les quotients successifs.
. En utilisant un tableur pour effectuer la division de 42 par 17, on obtient le tableau suivant. À partir de la cellule A2, la colonne A donne les restes successifs de la division de 42 par 17. À partir de la cellule B2, la colonne B donne les quotients successifs.a) Donner sans justification la 20e décimale de l'écriture décimale de 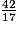 .
.
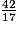 .
.b) À partir du tableau ci-contre, donner l'écriture décimale périodique de 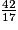 .
.
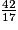 .
.c) Expliquer pourquoi on est sûr de retrouver dans la cellule A18 un reste déjà obtenu.
4. On se propose maintenant de retrouver l'écriture fractionnaire du rationnel a = 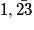 (c'est-à-dire le nombre dont l'écriture décimale périodique est 1,232323232323…). Pour cela, calculer 100a − a et en déduire l'écriture de a sous forme fractionnaire.
(c'est-à-dire le nombre dont l'écriture décimale périodique est 1,232323232323…). Pour cela, calculer 100a − a et en déduire l'écriture de a sous forme fractionnaire.
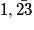 (c'est-à-dire le nombre dont l'écriture décimale périodique est 1,232323232323…). Pour cela, calculer 100a − a et en déduire l'écriture de a sous forme fractionnaire.
(c'est-à-dire le nombre dont l'écriture décimale périodique est 1,232323232323…). Pour cela, calculer 100a − a et en déduire l'écriture de a sous forme fractionnaire.Question complémentaire (4 points)
Cette question s'appuie sur les documents proposés en annexes 4 et 5.
Annexe 4 : Les réponses d'un élève à quatre exercices extraits de l'évaluation nationale à l'entrée en 6e de 2006 (Direction de l'évaluation, de la prospective et de la performance, ministère de l'Éducation nationale).
Annexe 5 : Extrait des programmes de mathématiques 2007 – cycle 3.
Annexe 4 : Les réponses d'un élève à quatre exercices extraits de l'évaluation nationale à l'entrée en 6e de 2006 (Direction de l'évaluation, de la prospective et de la performance, ministère de l'Éducation nationale).
Annexe 5 : Extrait des programmes de mathématiques 2007 – cycle 3.
1. Pour chacun des trois exercices 13, 15 et 26 (annexe 4), identifier de façon précise la capacité qu'il permet d'évaluer.
2. Identifier le type d'erreur effectué par cet élève (annexe 4) en analysant ses réponses.
Formuler deux hypothèses sur le mode opératoire utilisé par l'élève dans l'exercice 15.
Formuler deux hypothèses sur le mode opératoire utilisé par l'élève dans l'exercice 15.
3. Il est fréquent d'utiliser un tableau de numération (exemple ci-dessous) pour aider les élèves à effectuer des exercices tels que les exercices 13, 15 et 26.
Donner un avantage et un inconvénient liés à l'utilisation d'un tel tableau.
| 100 | 10 | 1 | 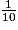 | 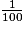 | 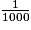 |
| centaines | dizaines | unités | dixièmes | centièmes | millièmes |
Donner un avantage et un inconvénient liés à l'utilisation d'un tel tableau.
4.
Un maître de CM2 a proposé l'exercice suivant à ses élèves. Le segment [AB] tracé sur papier millimétré a pour longueur 1 dm :
 |
a) En s'appuyant sur les programmes de cycle 3, identifier la connaissance relative à cet exercice.
b) Décrire une procédure qu'un élève de cycle 3 peut mettre en œuvre pour :
- tracer le segment attendu,
- écrire sa mesure sous forme décimale.
Annexe 1
 |
Annexe 2
 |
Annexe 3
 |
Annexe 4
 |
Annexe 5
 |
Corrigé
Corrigé
Exercice 1 (5 points)
1.
a) Dans le triangle SAB rectangle en A, on applique le théorème de Pythagore :
SB2 = SA2 + AB2
212 = SA2 + 142
Donc SA2 = 212 - 142 = 245
Donc SA =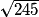 cm (valeur exacte) et SA
cm (valeur exacte) et SA 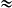 15,7 cm (valeur approchée au mm près).
15,7 cm (valeur approchée au mm près).
SB2 = SA2 + AB2
212 = SA2 + 142
Donc SA2 = 212 - 142 = 245
Donc SA =
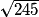 cm (valeur exacte) et SA
cm (valeur exacte) et SA 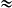 15,7 cm (valeur approchée au mm près).
15,7 cm (valeur approchée au mm près).b) Volume bougie = 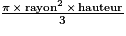
Volume bougie =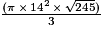
Volume bougie =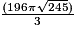 cm3 (valeur exacte)
cm3 (valeur exacte)
Volume bougie 3 212,682 cm3 (valeur approchée au mm3 près)
3 212,682 cm3 (valeur approchée au mm3 près)
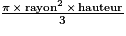
Volume bougie =
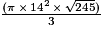
Volume bougie =
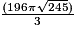 cm3 (valeur exacte)
cm3 (valeur exacte)Volume bougie
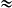 3 212,682 cm3 (valeur approchée au mm3 près)
3 212,682 cm3 (valeur approchée au mm3 près)c) 20 L = 20 dm3 = 20 000 cm3
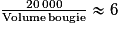
Avec 20 litres de cire, on peut fabriquer 6 bougies.
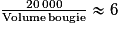
Avec 20 litres de cire, on peut fabriquer 6 bougies.
2.
a) Longueur de l'arc de cercle BB' = périmètre du cercle de rayon 14 cm = 2 × π × 14 = 28 π cm.
b) Angle α = 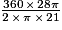 = 240°
= 240°
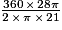 = 240°
= 240°3. La cire blanche a la forme d'un cône de révolution qui est la réduction d'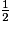 du cône de révolution de départ. Donc son volume est égale à
du cône de révolution de départ. Donc son volume est égale à 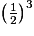 du volume de la bougie, soit
du volume de la bougie, soit 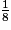 .
.
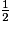 du cône de révolution de départ. Donc son volume est égale à
du cône de révolution de départ. Donc son volume est égale à 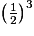 du volume de la bougie, soit
du volume de la bougie, soit 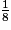 .
.Exercice 2 (3 points)
1. En multipliant le chiffre des unités de 50 000 006 et 70 000 008, on obtient 48.
Donc, on devrait lire 8 comme dernière décimale non nulle. Or sur la calculatrice on lit un 2, ce qui signifie que la valeur affichée sur l'écran n'est pas la valeur exacte de A.
Donc, on devrait lire 8 comme dernière décimale non nulle. Or sur la calculatrice on lit un 2, ce qui signifie que la valeur affichée sur l'écran n'est pas la valeur exacte de A.
2. A = 5,000 000 6 × 107 × 7,000 000 8 × 107
A = 5,000 000 × 7,000 000 8 × 107+7
A = 5,000 000 × 7,000 000 8 × 1014
Donc 5 × 7 x1014 < A < 6 × 8 × 1014
Soit 35 × 1014 < A < 48 × 1014
A = 5,000 000 × 7,000 000 8 × 107+7
A = 5,000 000 × 7,000 000 8 × 1014
Donc 5 × 7 x1014 < A < 6 × 8 × 1014
Soit 35 × 1014 < A < 48 × 1014
3. On applique la distributivité de la multiplication sur l'addition.
(5 × 107 ×6) ×(7 × 107 × 8) = 5 × 107 × 7 × 107 + 5 × 107 × 8 + 6 × 7 × 107 + 6 × 8
= 35 × 1014 + 40 × 107 + 42 × 107 + 48
= 35 × 1014 + 82 × 107 + 48
= 3 500 000 820 000 048
(5 × 107 ×6) ×(7 × 107 × 8) = 5 × 107 × 7 × 107 + 5 × 107 × 8 + 6 × 7 × 107 + 6 × 8
= 35 × 1014 + 40 × 107 + 42 × 107 + 48
= 35 × 1014 + 82 × 107 + 48
= 3 500 000 820 000 048
4. 48 506 × 505 = 24 495 530
557 × 505 = 281 285
48 506 × 149 = 7 227 394
557 × 149 = 82 993
557 × 505 = 281 285
48 506 × 149 = 7 227 394
557 × 149 = 82 993
B = (48 506 × 103 + 557) × (505 × 103 + 149)
B = 48 506 × 505 × 106 + 48 506 × 103 × 149 + 557 × 505 × 103 + 557 × 149
B = 24 495 530 × 106 + 7 227 394 × 103 + 281 285 × 103 + 82 993
B = 24 495 530 × 106 + 7 508 679 × 103 + 82 993
B = 24 495 530 000 000 + 7 508 761 993
B = 24 503 038 761 993
B = 48 506 × 505 × 106 + 48 506 × 103 × 149 + 557 × 505 × 103 + 557 × 149
B = 24 495 530 × 106 + 7 227 394 × 103 + 281 285 × 103 + 82 993
B = 24 495 530 × 106 + 7 508 679 × 103 + 82 993
B = 24 495 530 000 000 + 7 508 761 993
B = 24 503 038 761 993
Question complémentaire (4 points)
1.
a) L'élève peut taper une à une chaque addition. Cette procédure a pour inconvénient d'être longue et source d'erreurs mais elle permet à tous de participer, même aux élèves n'ayant pas encore compris dans la leçon 53 le sens de la multiplication. Sinon, l'élève peut faire appel au calcul mental en regroupant certains termes de l'addition ; il aura alors moins d'addition à taper sur la calculatrice et sera plus rapide, mais il peut avoir commis des fautes sur ces calculs intermédiaires.
b) Le fait d'imposer la calculatrice pour atteindre l'objectif « comprendre l'intérêt de transformer une addition réitérée en multiplication » permet de montrer aux élèves qu'avec la multiplication, on est plus rapide, et que l'on évite les erreurs de « frappe » dues aux successions d'additions.
2. Pour effectuer le 1er calcul, on peut faire : 25 + 25 = 50 ; puis 50 + 50 = 100 ; 100 + 100 + 25 = 225.
Cette procédure s'appuie sur le fait que 100 contient deux fois 50 et que 50 contient deux fois 25.
Pour le 2e calcul, l'élève a déjà rencontré dans l'application précédente des produits par 10 et l'impact de la multiplication par 10 sur le calcul. Il peut donc faire 38 × 10 = 80.
Cette procédure s'appuie sur le fait que 100 contient deux fois 50 et que 50 contient deux fois 25.
Pour le 2e calcul, l'élève a déjà rencontré dans l'application précédente des produits par 10 et l'impact de la multiplication par 10 sur le calcul. Il peut donc faire 38 × 10 = 80.
3.
| 3 + 3 + … + 3 21 fois | 3 × 21 | 21 + 21 + 21 3 fois | 3 × 10 + 3 × 10 + 3 |
Dans la première procédure, l'élève ajoute le nombre de cahiers, ici 3, de chaque élève et écrit une addition réitérée comme pour l'activité préparatoire de la leçon 54 (annexe 3).
Dans la seconde procédure, il remplace la multiplication réitérée précédente en une multiplication et utilise la leçon 54 (annexe 1).
Dans la troisième procédure, il se dit que la maîtresse donne un premier cahier à chaque élève, soit au total 21 cahiers ; puis qu'elle distribue un deuxième cahier à chacun, soit 21 cahiers ; puis qu'elle répète cette opération une troisième fois, soit encore 21 cahiers.
Dans la quatrième procédure, il réinvestit ce qu'il a vu sur l'impact de la multiplication par 10 sur un calcul.
Dans la seconde procédure, il remplace la multiplication réitérée précédente en une multiplication et utilise la leçon 54 (annexe 1).
Dans la troisième procédure, il se dit que la maîtresse donne un premier cahier à chaque élève, soit au total 21 cahiers ; puis qu'elle distribue un deuxième cahier à chacun, soit 21 cahiers ; puis qu'elle répète cette opération une troisième fois, soit encore 21 cahiers.
Dans la quatrième procédure, il réinvestit ce qu'il a vu sur l'impact de la multiplication par 10 sur un calcul.
Exercice 3 (4 points)
1. Les quotients de 27 par 8 et de 91 par 7 sont exacts. En effet, 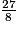 = 3,375 et
= 3,375 et 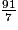 = 13.
= 13.
Donc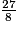 et
et 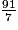 sont des nombres décimaux.
sont des nombres décimaux.
Par contre, les divisons de 1 par 7 et de 42 par 17 ne tombent pas justes, donc on ne peut donner que des valeurs approchées de ces quotients, et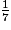 et
et 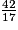 ne sont pas des nombres décimaux.
ne sont pas des nombres décimaux.
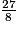 = 3,375 et
= 3,375 et 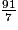 = 13.
= 13.Donc
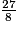 et
et 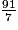 sont des nombres décimaux.
sont des nombres décimaux.Par contre, les divisons de 1 par 7 et de 42 par 17 ne tombent pas justes, donc on ne peut donner que des valeurs approchées de ces quotients, et
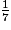 et
et 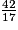 ne sont pas des nombres décimaux.
ne sont pas des nombres décimaux. 2.
a)
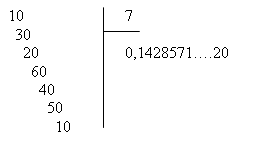 |
L'écriture décimale périodique de 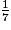 est 0,142857142857…
est 0,142857142857…
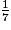 est 0,142857142857…
est 0,142857142857…b) La 6e décimale est 7 et c'est le cas toutes les 6 décimales, donc la 30e est 7, la 31e est 1 et la 32e est 4.
3.
a) La 20e décimale de l'écriture décimale périodique de 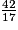 est 5.
est 5.
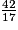 est 5.
est 5.b) 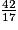 = 2,4705882352941176…
= 2,4705882352941176…
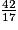 = 2,4705882352941176…
= 2,4705882352941176…c) 7 étant un nombre premier, le développement décimal de 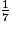 est périodique à partir d'un certain rang, au plus 7 − 1 = 6. En effet, les restes successifs sont par définition tous compris entre 1 et 7 − 1, et on va donc retomber à un moment sur le même reste (principe des tiroirs), donc sur le même quotient intermédiaire, et du coup sur la même suite de restes et quotients intermédiaires.
est périodique à partir d'un certain rang, au plus 7 − 1 = 6. En effet, les restes successifs sont par définition tous compris entre 1 et 7 − 1, et on va donc retomber à un moment sur le même reste (principe des tiroirs), donc sur le même quotient intermédiaire, et du coup sur la même suite de restes et quotients intermédiaires.
Au 2. b), on constate que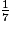 a un développement périodique de rang 6.
a un développement périodique de rang 6.
17 étant un nombre premier, et 42 et 17 étant premiers entre eux (PGCD (42 ; 17) = 1), le développement décimal de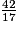 est périodique à partir d'un certain rang, au plus 17 − 1 = 16.
est périodique à partir d'un certain rang, au plus 17 − 1 = 16.
Or, dans la colonne A du tableau, on lit les restes successifs et on est sûr, au plus dans la case A18, de retomber sur un reste déjà obtenu.
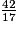 a un développement périodique de rang 16.
a un développement périodique de rang 16.
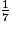 est périodique à partir d'un certain rang, au plus 7 − 1 = 6. En effet, les restes successifs sont par définition tous compris entre 1 et 7 − 1, et on va donc retomber à un moment sur le même reste (principe des tiroirs), donc sur le même quotient intermédiaire, et du coup sur la même suite de restes et quotients intermédiaires.
est périodique à partir d'un certain rang, au plus 7 − 1 = 6. En effet, les restes successifs sont par définition tous compris entre 1 et 7 − 1, et on va donc retomber à un moment sur le même reste (principe des tiroirs), donc sur le même quotient intermédiaire, et du coup sur la même suite de restes et quotients intermédiaires.Au 2. b), on constate que
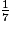 a un développement périodique de rang 6.
a un développement périodique de rang 6.17 étant un nombre premier, et 42 et 17 étant premiers entre eux (PGCD (42 ; 17) = 1), le développement décimal de
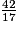 est périodique à partir d'un certain rang, au plus 17 − 1 = 16.
est périodique à partir d'un certain rang, au plus 17 − 1 = 16.Or, dans la colonne A du tableau, on lit les restes successifs et on est sûr, au plus dans la case A18, de retomber sur un reste déjà obtenu.
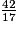 a un développement périodique de rang 16.
a un développement périodique de rang 16.4. 100a = 123,232323…
100a - a = 122? soit a(100 − 1) = 122
99a = 122
a =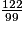
100a - a = 122? soit a(100 − 1) = 122
99a = 122
a =
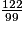
Question complémentaire (4 points)
1.
L'exercice 15 permet d'évaluer si l'élève connaît la valeur de chacun des chiffres composant une écriture à virgule, en fonction de sa position (ici les centièmes). Il s'agit aussi de voir si l'élève est capable de lier une décomposition utilisant 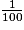 à une écriture à virgule.
à une écriture à virgule.
Pour l'exercice 26, la compétence évaluée est de savoir passer, dans un cas simple, pour un nombre décimal, d'une écriture fractionnaire (fraction décimale ici) à une écriture à virgule, et inversement pour l'exercice 13.
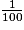 à une écriture à virgule.
à une écriture à virgule.Pour l'exercice 26, la compétence évaluée est de savoir passer, dans un cas simple, pour un nombre décimal, d'une écriture fractionnaire (fraction décimale ici) à une écriture à virgule, et inversement pour l'exercice 13.
L'exercice 35 permet de voir si l'élève sait que 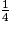 est une écriture fractionnaire de 0,25.
est une écriture fractionnaire de 0,25.
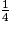 est une écriture fractionnaire de 0,25.
est une écriture fractionnaire de 0,25.Connaître les écritures fractionnaires 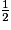 ,
, 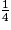 ,
, 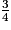 respectives des nombres décimaux 0.5, 0.25, 0.75 fait partie des connaissances attendues en fin de cycle 3.
respectives des nombres décimaux 0.5, 0.25, 0.75 fait partie des connaissances attendues en fin de cycle 3.
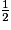 ,
, 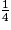 ,
, 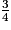 respectives des nombres décimaux 0.5, 0.25, 0.75 fait partie des connaissances attendues en fin de cycle 3.
respectives des nombres décimaux 0.5, 0.25, 0.75 fait partie des connaissances attendues en fin de cycle 3.2.
Aux exercices 13, 26 et 35, l'élève commet l'erreur de considérer un nombre décimal comme la juxtaposition de deux nombres entiers séparés par une virgule, la barre de fraction ne signifie rien pour cet élève. Pour lui, la virgule et la barre de fraction ont le même statut : séparer deux nombres entiers. Il ne voit la barre de fraction que comme une séparation entre le numérateur et le dénominateur, et n'a pas compris qu'elle signifie une division.
Pour l'exercice 15, on peut penser que l'élève additionne 96 et 2 et qu'il trouve 98. Puis il lit la fraction 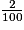 , il recopie le nombre 100 du dénominateur dans l'écriture décimale à droite de la virgule et entoure la réponse 98,100, ce qui est faux. Il commet une erreur semblable à ce qui a été dit ci-dessus pour les autres exercices.
, il recopie le nombre 100 du dénominateur dans l'écriture décimale à droite de la virgule et entoure la réponse 98,100, ce qui est faux. Il commet une erreur semblable à ce qui a été dit ci-dessus pour les autres exercices.
L'autre hypothèse est qu'au départ l'élève lit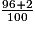 au lieu de 96 +
au lieu de 96 + 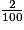 . Comme la barre de fraction n'a pas de sens pour lui, il considère peut-être que c'est la même chose.
. Comme la barre de fraction n'a pas de sens pour lui, il considère peut-être que c'est la même chose.
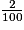 , il recopie le nombre 100 du dénominateur dans l'écriture décimale à droite de la virgule et entoure la réponse 98,100, ce qui est faux. Il commet une erreur semblable à ce qui a été dit ci-dessus pour les autres exercices.
, il recopie le nombre 100 du dénominateur dans l'écriture décimale à droite de la virgule et entoure la réponse 98,100, ce qui est faux. Il commet une erreur semblable à ce qui a été dit ci-dessus pour les autres exercices.L'autre hypothèse est qu'au départ l'élève lit
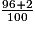 au lieu de 96 +
au lieu de 96 + 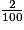 . Comme la barre de fraction n'a pas de sens pour lui, il considère peut-être que c'est la même chose.
. Comme la barre de fraction n'a pas de sens pour lui, il considère peut-être que c'est la même chose.3. Un avantage de ce tableau est de voir dans chacune des colonnes des écritures différentes d'un même nombre.
Le risque est que l'élève l'utilise mal. Par exemple, pour placer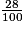 , voyant la colonne
, voyant la colonne 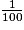 , il pourra faire l'erreur d'écrire dans cette case 28.
, il pourra faire l'erreur d'écrire dans cette case 28.
Le risque est que l'élève l'utilise mal. Par exemple, pour placer
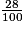 , voyant la colonne
, voyant la colonne 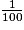 , il pourra faire l'erreur d'écrire dans cette case 28.
, il pourra faire l'erreur d'écrire dans cette case 28.4.
a) Dans cet exercice, il s'agit de voir si l'élève connaît le vocabulaire sur les fractions, ici le quart, et s'il sait utiliser cette fraction pour construire un segment.
b) Pour tracer le segment attendu, l'élève observe que [AB] est composé de 10 carreaux identiques. Il prend la moitié de [AB] et obtient un segment de 5 carreaux. Puis il reprend la moitié de ce nouveau segment et trouve que le segment cherché est un segment de 2 carreaux et demi.
Pour écrire la mesure du segment sous forme décimale, il va tout d'abord convertir 1 dm en 10 cm.
Puis il va diviser 10 par 2, obtenir 5 et enfin diviser 5 par 2 et trouver 2,5 cm.
Pour écrire la mesure du segment sous forme décimale, il va tout d'abord convertir 1 dm en 10 cm.
Puis il va diviser 10 par 2, obtenir 5 et enfin diviser 5 par 2 et trouver 2,5 cm.

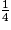 .
.