Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (4 points)
ABC est un triangle dans lequel l'angle de sommet A est aigu.
On considère le cercle de diamètre [BC]. Il coupe les droites (AB) et (AC) respectivement en D et E. Les droites (BE) et (CD) se coupent en H.
On considère le cercle de diamètre [BC]. Il coupe les droites (AB) et (AC) respectivement en D et E. Les droites (BE) et (CD) se coupent en H.
1. Faire une figure.
2. Démontrer que les droites (AH) et (BC) sont perpendiculaires.
3. Construire sur votre figure, avec la règle non graduée et le compas, le point M, quatrième sommet du parallélogramme BCMA et le point N, quatrième sommet du parallélogramme BCAN. On laissera les traits de construction apparents.
4. Démontrer que le point A est le milieu de [MN].
Question complémentaire (3 points)
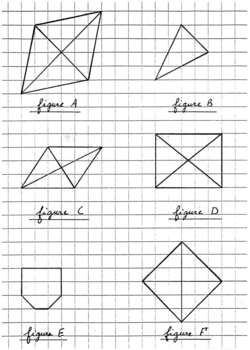
Vous trouverez en annexe 1 une collection de 6 figures à partir de laquelle un enseignant propose le jeu du portrait suivant à ses élèves de CM2 :
J'ai quatre sommets,
mes diagonales ne sont pas perpendiculaires,
mes côtés n'ont pas tous la même longueur,
je possède au moins un angle droit.
Qui suis-je ?
Tu dois répondre par une lettre : figure…
J'ai quatre sommets,
mes diagonales ne sont pas perpendiculaires,
mes côtés n'ont pas tous la même longueur,
je possède au moins un angle droit.
Qui suis-je ?
Tu dois répondre par une lettre : figure…
1. Est-il possible de supprimer une ligne (ou une phrase) dans ce jeu du portrait sans incidence sur la réponse attendue ? Si oui, laquelle ? Justifiez précisément votre réponse.
2. Relevez deux difficultés liées à la formulation des phrases utilisées dans ce jeu du portrait.
3. En vous référant à l'annexe 2, citez une connaissance et une capacité travaillées lors de cette activité.
4. Les figures sont présentées sur un support quadrillé. Indiquez deux conséquences, liées au choix de ce support, sur les procédures des élèves.
Exercice 2 (4 points)
Pour carreler une pièce rectangulaire mesurant 4,18 m sur 5,67 m, un carreleur propose à des propriétaires le choix entre deux modèles de dalles carrées :
1.
Le premier modèle a 29 cm de côté et coûte 2,30 € l'unité. Avec ce modèle, il n'utilise que des dalles entières et il complète avec du joint autour de chaque dalle.
a)
Calculer le nombre maximal de dalles que l'on peut poser dans la largeur de la pièce.b)
Calculer le nombre maximal de dalles que l'on peut poser dans la longueur de la pièce.c)
Les joints autour des dalles auront-ils tous la même largeur ? Si oui, quelle est cette largeur ?2. Le deuxième modèle a 36 cm de côté et coûte 3,10 € l'unité.
Avec ce modèle-là, il est préconisé des joints de 0,6 cm et le carreleur est alors dans l'obligation de couper des dalles et les découpes ne sont pas réutilisées.
Calculer le nombre de dalles nécessaires.
Avec ce modèle-là, il est préconisé des joints de 0,6 cm et le carreleur est alors dans l'obligation de couper des dalles et les découpes ne sont pas réutilisées.
Calculer le nombre de dalles nécessaires.
3. Quel sera le choix le moins coûteux pour l'achat des dalles ?
Question complémentaire (5 points)
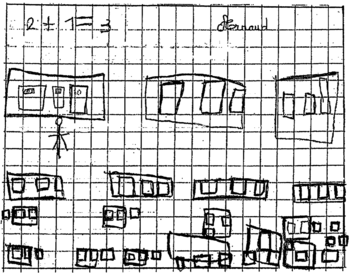
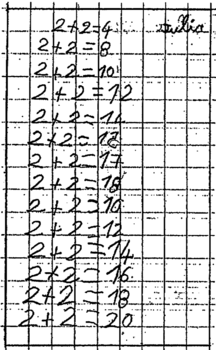
Les productions d'élèves figurent aux annexes 3a et 3b.
Au début de l'année, dans une classe de CE1, le maître a proposé le problème suivant :
Dans une classe de 19 élèves, le maître distribue des livres et des cahiers. Chaque élève reçoit 2 cahiers et 1 livre. Combien de cahiers le maître a-t-il distribués en tout ?
L'énoncé étant écrit au tableau, une lecture silencieuse des élèves puis une lecture orale du maître ont été effectuées.
Au début de l'année, dans une classe de CE1, le maître a proposé le problème suivant :
Dans une classe de 19 élèves, le maître distribue des livres et des cahiers. Chaque élève reçoit 2 cahiers et 1 livre. Combien de cahiers le maître a-t-il distribués en tout ?
L'énoncé étant écrit au tableau, une lecture silencieuse des élèves puis une lecture orale du maître ont été effectuées.
1. Citer deux difficultés que présente cet énoncé de problème pour des élèves de début de CE1.
2.
a) Les productions de cinq élèves sont reproduites dans les annexes 3a et 3b. Pour chaque élève, décrire la procédure mise en œuvre et repérer les éventuelles erreurs.
b) Le maître décide de regrouper Adeline et Wassim d'une part, et Arnaud, Thomas et Julia d'autre part. Expliquer ce choix au regard des procédures mises en œuvre par les élèves.
3. À la suite de ce travail, le maître décide d'introduire l'écriture multiplicative. Indiquer deux idées principales qui doivent apparaître dans une trace écrite.
Exercice 3 (4 points)
1. Un nombre de trois chiffres est tel que :
- la somme de ses trois chiffres est égale à 14 ;
- ce nombre est plus grand que son nombre « retourné » (exemple : si le nombre est 651, son nombre « retourné » est 156) ;
- la différence entre ce nombre et son nombre « retourné » est 99 ;
- la différence entre le double du chiffre des dizaines et le triple du chiffre des centaines est égale à 2.
2.
En observant les nombres 297, 880 et 242, un élève a formulé la conjecture « tout nombre à trois chiffres dans lequel le chiffre des dizaines est la somme du chiffre des centaines et du chiffre des unités est divisible par 11 ».
a) Cette conjecture s'applique-t-elle au nombre trouvé à la question 1 ?
b) La conjecture de l'élève est-elle effectivement vraie ? Justifier la réponse.
c) Trouver un nombre de 3 chiffres qui soit divisible par 11 et dans lequel le chiffre des dizaines n'est pas la somme du chiffre des centaines et de celui des unités.
Annexe 1
 |
Annexe 2
 |
Annexe 3
 |
 |
 |
 |
 |
Corrigé
Corrigé
Exercice 1 (4 points)
1.
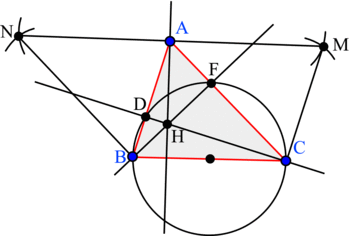 |
2. CEB est un triangle rectangle en E car il est inscrit dans un demi-cercle de diamètre [CB].
Donc (EB) est perpendiculaire à (AC).
CDB est un triangle rectangle en D car il est inscrit dans un demi-cercle de diamètre [CB].
Donc (CD) est perpendiculaire à (AB).
On en déduit que (EB) et (CD) sont deux hauteurs du triangle ABC. Elles se coupent en H.
Le point H est donc l'orthocentre du triangle ABC.
(AH) est une droite qui passe par le sommet A du triangle ABC et par l'orthocentre H, donc (AH) est la 3e hauteur du triangle ABC. Elle est par définition perpendiculaire au côté opposé à A, c'est-à-dire le côté [BC].
Donc (EB) est perpendiculaire à (AC).
CDB est un triangle rectangle en D car il est inscrit dans un demi-cercle de diamètre [CB].
Donc (CD) est perpendiculaire à (AB).
On en déduit que (EB) et (CD) sont deux hauteurs du triangle ABC. Elles se coupent en H.
Le point H est donc l'orthocentre du triangle ABC.
(AH) est une droite qui passe par le sommet A du triangle ABC et par l'orthocentre H, donc (AH) est la 3e hauteur du triangle ABC. Elle est par définition perpendiculaire au côté opposé à A, c'est-à-dire le côté [BC].
3. Voir figure.
4.
BCMA étant un parallélogramme, ses côtés opposés ont la même longueur, donc BC = AM.
BCAN est un parallélogramme, donc BC = AN.
Donc AM = AN.
BCAN est un parallélogramme, donc BC = AN.
Donc AM = AN.
De plus, BCMA étant un parallélogramme, ses côtés opposés sont parallèles deux à deux, donc (BC) est parallèle à (MA).
BCAN est un parallélogramme, donc (BC) est parallèle à (NA).
On en déduit que (MA) est parallèle à (NA), donc A (MN).
(MN).
BCAN est un parallélogramme, donc (BC) est parallèle à (NA).
On en déduit que (MA) est parallèle à (NA), donc A
 (MN).
(MN).AM = AN et A  (MN), donc A est le milieu de [MN].
(MN), donc A est le milieu de [MN].
 (MN), donc A est le milieu de [MN].
(MN), donc A est le milieu de [MN].Question complémentaire (3 points)
1. On peut enlever la ligne « j'ai quatre sommets » sans incidence sur la réponse car ensuite on lit : « mes diagonales ne sont pas perpendiculaires ». L'utilisation du mot « perpendiculaires » sous-entend qu'il y a deux diagonales et que par conséquent la figure est un quadrilatère.
2. Une première difficulté réside dans l'utilisation à deux reprises d'une formulation négative :« mes diagonales ne sont pas perpendiculaires » et « mes côtés n'ont pas tous la même longueur ».
La deuxième difficulté réside dans l'utilisation de « au moins » à la ligne « je possède au moins un angle droit ».
La deuxième difficulté réside dans l'utilisation de « au moins » à la ligne « je possède au moins un angle droit ».
3. Dans cette activité, l'élève travaille ses connaissances sur les figures planes. Il doit connaître et savoir utiliser le vocabulaire spécifique : perpendiculaires, sommets, côtés, angle, etc.
Cette activité mobilise sa capacité à reconnaître de manière perceptive une figure plane, à en donner le nom, à vérifier son existence en ayant recours aux propriétés et aux instruments.
Cette activité mobilise sa capacité à reconnaître de manière perceptive une figure plane, à en donner le nom, à vérifier son existence en ayant recours aux propriétés et aux instruments.
4. Les figures étant proposées sur papier quadrillé, les élèves n'utiliseront ni l'équerre pour vérifier la perpendicularité, ni la règle pour identifier des longueurs égales ; ils s'aideront des carreaux.
Exercice 2 (4 points)
1.
a) Nombre de dalles entières dans la largeur = 4,18 ÷ 0,29 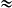 14.
14.
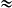 14.
14.b) Nombre de dalles entières dans la longueur = 6,67 ÷ 0,29 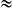 19.
19.
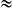 19.
19.c) En largeur : 14 × 0,29 = 4,06.
Il reste 0,12 m pour faire 15 joints.
0,12 ÷ 15 = 0,008 m = 8 mm.
Les joints auront tous une même largeur de 8 mm.
Il reste 0,12 m pour faire 15 joints.
0,12 ÷ 15 = 0,008 m = 8 mm.
Les joints auront tous une même largeur de 8 mm.
2.
Nombre de dalles dans la largeur = 4,18 ÷ 0,36 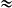 11,6.
11,6.
Pour la largeur, on achètera 12 dalles. 11 dalles seront posées entières et 1 sera découpée. Il faut donc faire 13 joints. 13 × 0,006 + 11 × 0,36 = 4,038 m.
4,18 − 4,038 = 0,142 m.
La longueur de la 12e dalle découpée sera de 0,142 m.
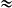 11,6.
11,6.Pour la largeur, on achètera 12 dalles. 11 dalles seront posées entières et 1 sera découpée. Il faut donc faire 13 joints. 13 × 0,006 + 11 × 0,36 = 4,038 m.
4,18 − 4,038 = 0,142 m.
La longueur de la 12e dalle découpée sera de 0,142 m.
Nombre de dalles dans la longueur = 5,67 ÷ 0,36 = 15,75.
Pour la longueur, on achètera 16 dalles. 15 dalles seront posées entières et 1 sera découpée. Il faut donc faire 17 joints. 17 × 0,006 + 15 × 0,36 = 5,502 m.
5,67 − 5,502 = 0,168 m.
La longueur de la 16e dalle découpée sera de 0,168 m.
Pour la longueur, on achètera 16 dalles. 15 dalles seront posées entières et 1 sera découpée. Il faut donc faire 17 joints. 17 × 0,006 + 15 × 0,36 = 5,502 m.
5,67 − 5,502 = 0,168 m.
La longueur de la 16e dalle découpée sera de 0,168 m.
Nombre total de dalles = 16 × 12 = 192.
3. Premier modèle : 14 × 19 = 266 dalles. Coût = 266 × 2,30 = 611,8 €.
Deuxième modèle : Coût = 192 × 3,10 = 595,2 €.
Donc le choix le moins coûteux est d'acheter les dalles du 2e modèle.
Deuxième modèle : Coût = 192 × 3,10 = 595,2 €.
Donc le choix le moins coûteux est d'acheter les dalles du 2e modèle.
Question complémentaire (5 points)
1. Une première difficulté réside dans le fait que la question posée ne porte pas sur tout ce qui a été distribué. Toutes les données numériques ne servent pas à résoudre le problème.
Une deuxième difficulté tient au fait qu'il y a 19 élèves dans la classe et qu'au moment de la résolution, les élèves auront une retenue en posant l'addition 19 + 19.
Une deuxième difficulté tient au fait qu'il y a 19 élèves dans la classe et qu'au moment de la résolution, les élèves auront une retenue en posant l'addition 19 + 19.
2.
a) Arnaud calcule le nombre de cahiers et de livres par élève (2 + 1 = 3) et représente chacun des élèves de la classe avec ses 2 cahiers et son livre. Il représente 18 élèves et non 19. On peut penser qu'il ne se représente pas lui-même. Ces dessins faits, il ne propose pas de réponse à la question posée. Mais on peut tout de même penser qu'il a lu, comme question, « Combien de cahiers et de livres le maître a-t-il distribués en tout », et non « Combien de cahiers le maître a-t-il distribués en tout ».
Wassim pose l'addition 19 + 19 et trouve 38, qui est une bonne réponse.
Thomas trouve aussi la bonne réponse en réalisant une représentation des 19 élèves qui auront chacun 2 cahiers.
Adeline écrit 1 + 1 = 2, soit 2 cahiers pour le 1er élève. Puis elle cherche combien de cahiers sont distribués à 2 élèves en écrivant 2 + 2 = 4, puis à 4 élèves en écrivant 4 + 4 = 8, puis à 5 élèves en écrivant 5 + 5 = 10. Sa démarche est bonne mais longue. D'ailleurs, on peut penser qu'elle n'a pas fini sa recherche.
Julia a bien lu que chaque élève reçoit 2 cahiers mais elle écrit une succession d'additions avec le chiffre 2. Elle n'a pas acquis le sens du symbole « + ».
Wassim pose l'addition 19 + 19 et trouve 38, qui est une bonne réponse.
Thomas trouve aussi la bonne réponse en réalisant une représentation des 19 élèves qui auront chacun 2 cahiers.
Adeline écrit 1 + 1 = 2, soit 2 cahiers pour le 1er élève. Puis elle cherche combien de cahiers sont distribués à 2 élèves en écrivant 2 + 2 = 4, puis à 4 élèves en écrivant 4 + 4 = 8, puis à 5 élèves en écrivant 5 + 5 = 10. Sa démarche est bonne mais longue. D'ailleurs, on peut penser qu'elle n'a pas fini sa recherche.
Julia a bien lu que chaque élève reçoit 2 cahiers mais elle écrit une succession d'additions avec le chiffre 2. Elle n'a pas acquis le sens du symbole « + ».
b) Adeline et Wassim ont réussi à traduire la question posée par une ou plusieurs opérations correctes. Ils ont acquis le sens de l'addition.
Arnaud, Thomas et Julia, eux, n'ont pas réussi à écrire un calcul traduisant la question posée. Ils n'ont réalisé que des représentations de la situation. Julia, en écrivant 2 + 2 = 4 puis 2 + 2 = 8, 2 + 2 = 10, etc., utilise le symbole « + » comme un symbole séparant les deux chiffres, de même que Thomas tire un trait entre deux bâtons.
Arnaud, Thomas et Julia, eux, n'ont pas réussi à écrire un calcul traduisant la question posée. Ils n'ont réalisé que des représentations de la situation. Julia, en écrivant 2 + 2 = 4 puis 2 + 2 = 8, 2 + 2 = 10, etc., utilise le symbole « + » comme un symbole séparant les deux chiffres, de même que Thomas tire un trait entre deux bâtons.
3. Dans la trace de cours, le maître montrera l'intérêt de transformer une addition réitérée en multiplication. Il fera apparaître que la multiplication permet de remplacer plusieurs additions en une seule opération et donc d'être plus rapide. Par ailleurs, il fera remarquer qu'écrire des additions successives a pour inconvénient d'être une méthode longue et source d'erreurs de calcul (ce qui est le cas pour Julia).
Exercice 3 (4 points)
1.
Soit xyz le nombre cherché, tel que xyz > zyx.
xyz − zyx = 99 conduit à x − z = 1.
On résout le système suivant :
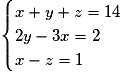
xyz − zyx = 99 conduit à x − z = 1.
On résout le système suivant :
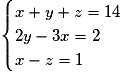
On remplace x = z + 1 dans la 1re équation.
(z + 1) + y + z = 14
2z + y = 13, d'où y = 13 − 2z.
(z + 1) + y + z = 14
2z + y = 13, d'où y = 13 − 2z.
On remplace x = z + 1 dans la 2e équation.
2y − 3(z + 1) = 2
2y − 3z − 3 = 2
2y − 3z = 5.
2y − 3(z + 1) = 2
2y − 3z − 3 = 2
2y − 3z = 5.
On résout : 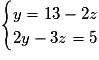
2(13−2z) − 3z = 5
21 = 7z, d'où z =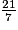 = 3.
= 3.
x = z + 1 = 3 + 1 = 4.
4 + y + 3 = 14, d'où y = 7.
Donc le nombre cherché est 473.
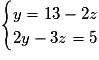
2(13−2z) − 3z = 5
21 = 7z, d'où z =
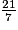 = 3.
= 3.x = z + 1 = 3 + 1 = 4.
4 + y + 3 = 14, d'où y = 7.
Donc le nombre cherché est 473.
2.
a) 473 est un nombre à 3 chiffres tel que le chiffre des dizaines est égal à la somme des chiffres des centaines et des unités (3 + 4 = 7).
Et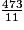 = 43, c'est-à-dire que 473 est divisible par 11.
= 43, c'est-à-dire que 473 est divisible par 11.
Donc la conjecture de l'élève s'applique bien à 473.
Et
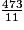 = 43, c'est-à-dire que 473 est divisible par 11.
= 43, c'est-à-dire que 473 est divisible par 11.Donc la conjecture de l'élève s'applique bien à 473.
b) Soit abc un nombre à 3 chiffres tel que b = a + c.
Montrons que ce nombre abc est divisible par 11.
abc = c × 1 + b × 10 + a × 100
= c × 1 + (a + c ) × 10 + a × 100
= c × 1 + a × 10 + c × 10 + a × 100
= c × (1 + 10) + a × (10 + 100)
= c × 11 + a × 110
= ac × 11
Donc abc étant égal au produit de 11 par un nombre entier, abc est divisible par 11.
Montrons que ce nombre abc est divisible par 11.
abc = c × 1 + b × 10 + a × 100
= c × 1 + (a + c ) × 10 + a × 100
= c × 1 + a × 10 + c × 10 + a × 100
= c × (1 + 10) + a × (10 + 100)
= c × 11 + a × 110
= ac × 11
Donc abc étant égal au produit de 11 par un nombre entier, abc est divisible par 11.
c) 209 est un nombre à 3 chiffres qui est divisible par 11, car 209 = 11 × 19. Pourtant, son chiffre des dizaines n'est pas égal à la somme du chiffre des centaines et du chiffre des unités (2 + 9 = 11 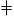 0 ).
0 ).
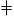 0 ).
0 ). 