Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (4 points)
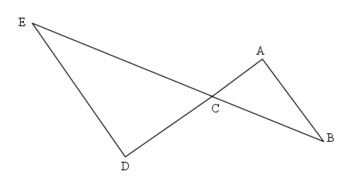
On considère cinq points A, B, C, D et E tels que :
- Le triangle CAB est rectangle en A.
- Les points A, C, D sont alignés. AC = 3 cm ; AD = 8,4 cm.
- Les points B, C, E sont alignés. BC = 4,5 cm ; BE = 12,6 cm.
 |
1.
a) Démontrer que les droites (AB) et (ED) sont parallèles.
b) En déduire que les angles  et
et 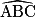 sont égaux.
sont égaux.
 et
et 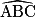 sont égaux.
sont égaux.2.
a) Déterminer l'aire du triangle ABC. En donner son arrondi au cm2 près.
b) On admet que le triangle CED est un agrandissement du triangle ABC. En déduire, sans calculer la longueur ED, l'aire du triangle EDC.
Exercice 2 (2, 5 points)
Jacques est confiseur et veut réaliser des assortiments de lirettes au chocolat et de contettes au praliné.
Il a fabriqué 1386 lirettes et 308 contettes.
Il veut faire des sachets de la manière suivante :
Il a fabriqué 1386 lirettes et 308 contettes.
Il veut faire des sachets de la manière suivante :
- chaque sachet contient le même nombre de lirettes ;
- chaque sachet contient le même nombre de contettes ;
- toutes les confiseries doivent être contenues dans les sachets.
1.
Combien de sachets peut-il réaliser au plus ?2.
Quel sera alors le nombre de lirettes et de contettes dans chaque sachet ?3.
Si toutes les lirettes et toutes les contettes étaient dans un même récipient, sans regarder, combien Jacques devrait-il prendre au minimum de confiseries pour être sûr d'avoir au moins une lirette et au moins une contette ?Question complémentaire (4 points)
Annexe 1 : Productions d'élèves, exercice extrait du manuel « Vivre les maths » CE2 2005 Nathan.
1.
L'énoncé proposé aux élèves est le suivant :
Sur l'étagère de fournitures de la classe, il y a 8 piles de 10 cahiers plus 9 cahiers. Quel est le nombre de cahiers ?
Cet énoncé comporte une ambiguïté qui peut mener à deux résultats différents.
Sur l'étagère de fournitures de la classe, il y a 8 piles de 10 cahiers plus 9 cahiers. Quel est le nombre de cahiers ?
Cet énoncé comporte une ambiguïté qui peut mener à deux résultats différents.
a) Quelle est cette ambiguïté ? Quels sont les deux résultats que l'on peut obtenir ?
b) Proposer un nouvel énoncé permettant de lever cette ambiguïté pour obtenir 89 cahiers comme seule réponse possible.
2.
Comparer les productions des élèves A et C. Décrire l'erreur de l'élève B et fournir une hypothèse qui pourrait l'expliquer.
3.
Proposer un nouvel énoncé (dans le même contexte) qui obligerait l'élève A à modéliser la situation de la même manière que l'élève C.
4.
Fournir deux pistes de travail à envisager avec l'élève B pour l'aider à surmonter ses difficultés.
Exercice 3 (3 points)
Lucie et Marc participent à une compétition de tir à l'arc. Dans le tableau ci-dessous, on trouve les scores partiels des 8 tours de volées de 3 flèches. (10 est le score parfait pour une flèche).
| Tour 1 | Tour 2 | Tour 3 | Tour 4 | Tour 5 | Tour 6 | Tour 7 | Tour 8 | Moyenne | |
| Lucie | x | y | 29 | 12 | 26 | 27 | 17 | 25 | 23 |
| Marc | 18 | 28 | 12 | 29 | 26 | 19 | 22 |
1.
Calculer la moyenne des scores de Marc si le score obtenu au tour 3 est égal à la moyenne des sept tours déjà notés dans le tableau.2.
Une performance meilleure au tour 3 lui aurait-elle permis d'obtenir une moyenne supérieure ou égale à celle de Lucie ? Justifier.3.
Le score x obtenu par Lucie au premier tour est supérieur de 40 % au score y qu'elle a obtenu au second tour.Après avoir exprimé x en fonction de y, calculer x et y.
Exercice 4 (2, 5 points)
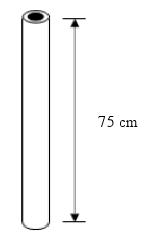 |
On a représenté ci-contre un tube creux en aluminium en perspective.
Son diamètre intérieur est 8 cm, son diamètre extérieur est 12 cm.
L'aluminium a une masse volumique de 2,7 g/ cm3.
On veut transporter un certain nombre de ces tubes dans un camion dont la charge utile ne peut dépasser 14 tonnes.
En supposant que le volume du camion est suffisant, combien peut-on transporter de tubes au maximum ?
On utilisera 3,14 comme valeur approchée de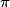 .
.
On rappelle que le volume d'un cylindre est donné par : V =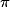 × r2 × h, où r désigne le rayon de la base et h la hauteur du cylindre.
× r2 × h, où r désigne le rayon de la base et h la hauteur du cylindre.
Son diamètre intérieur est 8 cm, son diamètre extérieur est 12 cm.
L'aluminium a une masse volumique de 2,7 g/ cm3.
On veut transporter un certain nombre de ces tubes dans un camion dont la charge utile ne peut dépasser 14 tonnes.
En supposant que le volume du camion est suffisant, combien peut-on transporter de tubes au maximum ?
On utilisera 3,14 comme valeur approchée de
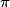 .
.On rappelle que le volume d'un cylindre est donné par : V =
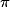 × r2 × h, où r désigne le rayon de la base et h la hauteur du cylindre.
× r2 × h, où r désigne le rayon de la base et h la hauteur du cylindre.Question complémentaire (4 points)
Le document présenté en annexe 2-A est tiré de « J'apprends les maths - CE2 », Éditions Retz. L'annexe 2-B présente la production d'un élève.
1.
Pour cette question, se reporter au document reproduit en annexe 2-A.
a) Citer deux difficultés que peuvent rencontrer les élèves pour barrer les masses impossibles de l'exercice 1.
b) Citer deux difficultés que peuvent rencontrer les élèves pour répondre correctement à l'exercice 2-A.
2.
Pour cette question, se reporter au document reproduit en annexe 2-B.
a) Dans cette question on s'intéresse aux exercices 2.a), 2.b) et 2.c). Quelle est la règle implicite utilisée par cet élève ?
b) Dans cette question on s'intéresse à l'exercice 2.d). Lorsqu'il s'agit de transformer une écriture en gramme en une écriture complexe kilogramme-gramme, on peut supposer que l'élève utilise la règle implicite suivante : le premier chiffre correspond au nombre de kilogrammes, le reste des chiffres correspond au nombre de grammes. Proposer un exercice (dans le même contexte) qui permettrait de vérifier si l'élève utilise cette règle qui donne en général un résultat faux.
3.
Pour cette question, se reporter au document reproduit en annexe 2-B.
a) Comment utiliser des masses marquées et une balance à affichage digital pour faire prendre conscience à l'élève de son erreur lors de l'écriture de l'égalité :
2 kg 40 g = 240 g ?
2 kg 40 g = 240 g ?
b) Donner une aide possible que l'enseignant peut apporter à cet élève.
Annexe 1
 |
Annexe 2-A
 |
Annexe 2-B
 |
Corrigé
Corrigé
Exercice 1 (4 points)
1.
a) (EB) et (AD) sont sécantes en C.
E, C, B et D, C, A sont des points distincts et alignés dans le même ordre.
CD ÷ AC = 5, 4 ÷ 3 = 1, 8
CE ÷ CB = 8, 1 ÷ 4, 5 = 1, 8
Donc CD ÷ AC = CE ÷ CB
Donc d'après la propriété réciproque de Thalès, les droites (AB) et (ED) sont parallèles.
E, C, B et D, C, A sont des points distincts et alignés dans le même ordre.
CD ÷ AC = 5, 4 ÷ 3 = 1, 8
CE ÷ CB = 8, 1 ÷ 4, 5 = 1, 8
Donc CD ÷ AC = CE ÷ CB
Donc d'après la propriété réciproque de Thalès, les droites (AB) et (ED) sont parallèles.
b) (AB) et (ED) sont deux droites coupées par une sécante (EB).
Dans cette configuration, les angles et
et  sont des angles alternes-internes.
sont des angles alternes-internes.
Or d'après 1., (AB) et (ED) sont deux droites parallèles donc ces angles alternes-internes sont égaux.
Dans cette configuration, les angles
 et
et  sont des angles alternes-internes.
sont des angles alternes-internes.Or d'après 1., (AB) et (ED) sont deux droites parallèles donc ces angles alternes-internes sont égaux.
2.
a) Aire de ABC = (base × hauteur) ÷ 2 = (AC × AB)
Calcul de AB :
Dans ABC rectangle en A, on applique le théorème de Pythagore :
AB2 = BC2 − AC2 = 4,52 − 32 = 11, 25
On en déduit que Aire de ABC = (3 ×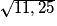 ) ÷2
) ÷2 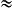 5 cm2
5 cm2
Calcul de AB :
Dans ABC rectangle en A, on applique le théorème de Pythagore :
AB2 = BC2 − AC2 = 4,52 − 32 = 11, 25
On en déduit que Aire de ABC = (3 ×
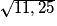 ) ÷2
) ÷2 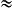 5 cm2
5 cm2b) ED = 1, 8 × AB
Or dans un agrandissement de coefficient 1, 8, les aires sont multipliées par le coefficient au carré c'est-à-dire ici 1,82.
Donc Aire de EDC = 1,82 × Aire de ABC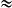 16, 2 cm2.
16, 2 cm2.
Or dans un agrandissement de coefficient 1, 8, les aires sont multipliées par le coefficient au carré c'est-à-dire ici 1,82.
Donc Aire de EDC = 1,82 × Aire de ABC
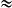 16, 2 cm2.
16, 2 cm2.Exercice 2 (2, 5 points)
1.
On cherche le PGCD de 1386 et 308 par l'algorithme d'Euclide :1386 = 308 × 4 + 154
308 = 154 × 2 + 0
Le PGCD est le dernier reste non nul, ici 154.
2.
1386 ÷ 154 = 9308 ÷ 154 = 2
Dans chaque sachet, on compte 9 lirettes et de 2 contettes.
3.
Si toutes les lirettes et toutes les contettes étaient dans un même récipient, sans regarder, Jacques devrait prendre au minimum 309 confiseries pour être sûr d'avoir au moins une lirette et au moins une contette car dans le pire des cas il peut tirer au hasard 308 fois d'affiler une contette.Question complémentaire (4 points)
1.
a) L'ambiguïté est qu'il y a écrit « 8 piles de 10 cahiers plus 9 cahiers » et non « 8 piles de 10 cahiers chacune et une pile de 9 cahiers ».
Un résultat que l'on peut obtenir est 152 si l'on comprend à la lecture de l'énoncé 8 piles de 19 cahiers et 8 × 19 = 152.
Si l'on comprend « 8 piles de 10 cahiers chacune et une pile de 9 cahiers », on obtiendra 89 en faisant 8 × 10 + 9.
Un résultat que l'on peut obtenir est 152 si l'on comprend à la lecture de l'énoncé 8 piles de 19 cahiers et 8 × 19 = 152.
Si l'on comprend « 8 piles de 10 cahiers chacune et une pile de 9 cahiers », on obtiendra 89 en faisant 8 × 10 + 9.
b) Un énoncé permettant de lever cette ambiguïté pour obtenir 89 cahiers comme seule réponse possible serait par exemple :
« Sur l'étagère de fournitures de la classe, il y a 8 piles de 10 cahiers chacune et une pile 9 cahiers uniquement. Quel est le nombre de cahiers ? »
« Sur l'étagère de fournitures de la classe, il y a 8 piles de 10 cahiers chacune et une pile 9 cahiers uniquement. Quel est le nombre de cahiers ? »
2.
Les élèves A et C ont tous les deux de bonnes productions et le bon résultat. L'élève A utilise des additions réitérées 10 + 10…, 8 fois de suite tandis que l'élève C connaît le sens de la multiplication et écrit à la place 8 × 10.L'erreur de l'élève B est d'additionner tous les nombres qu'il rencontre dans l'énoncé sans s'occuper de la nature des objets et du sens des opérations, il additionne ainsi un nombre de piles et des nombres de cahiers.
Une hypothèse qui pourrait expliquer son erreur est qu'il ne connaît pas le sens de l'expression « pile de cahiers ».
3.
Un nouvel énoncé qui obligerait l'élève A à modéliser la situation de la même manière que l'élève C serait : « Sur l'étagère de fournitures de la classe, il y a 80 piles de 10 cahiers chacune et une pile de 9 cahiers uniquement. Quel est le nombre de cahiers ? ».En changeant 8 piles de 10 cahiers par 80 piles de 10 cahiers, l'addition réitérée 10 + 10 … +10 devient très très longue et source d'erreur et poussera l'élève A à modéliser la situation par la multiplication 80 × 10.
4.
Une première piste de travail à envisager avec l'élève B serait de travailler sur le vocabulaire utilisé dans les énoncés et de lui faire faire une représentation schématique de la situation.La deuxième piste serait de le faire travailler sur le fait que l'on ne peut pas additionner des nombres d'objets de nature différente. Il pourrait alors souligner dans le texte les nombres désignant les cahiers et le nombre de piles de couleurs distinctes.
Exercice 3 (3 points)
1.
(18 + 28 + 12 + 29 + 26 + 19 + 22) ÷ 7 = 22La moyenne est égale à 22.
On remplace la 3e note par 22 :
(18 + 28 + 22 + 12 + 29 + 26 + 19 + 22) ÷ 8 = 22.
2.
(18 + 28 + 30 + 12 + 29 + 26 + 19 + 22) ÷ 8 = 23.3.
x = y (1 + 40 ÷100) = 1,4y(y + 1,4y + 29 + 12 + 26 + 27 + 17 + 25) ÷ 8 = 23
(2,4y + 136) ÷ 8 = 23
0,3y + 17 = 23
y = (23 − 17) ÷ 0,3 = 20
et x = 1,4 × 20 = 28.
Exercice 4 (2, 5 points)
On utilise la formule du volume du cylindre droit :Volume cylindre = aire du disque × hauteur du cylindre
Volume d'un tube = 3,14 × 6 × 6 × 75 − 3,14 × 4 × 4 × 75
Volume d'un tube = 4710 cm3
Masse d'un tube = 2,7 × 4710 = 12 717 g = 12, 717 kg
1 tonne = 1000 kg
Nombre de tubes = 14 000 ÷ 12, 717
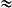 1100.
1100.Question complémentaire (4 points)
1.
a) Une difficulté que peuvent rencontrer les élèves pour barrer les masses est que celles-ci ne sont pas toutes exprimées en grammes. Certains élèves auront du mal à convertir 15 kg en g ou 1 kg 500 g en g par exemple.
Une autre difficulté, pour ces élèves, est de devoir imaginer des masses sans pouvoir sous peser réellement l'objet en question.
Une autre difficulté, pour ces élèves, est de devoir imaginer des masses sans pouvoir sous peser réellement l'objet en question.
b) Pour répondre à l'exercice 2.a), les élèves peuvent :
- avoir des difficultés pour comparer des masses qui ne sont pas dans la même unité.
- commettre des erreurs liées à une mauvaise connaissance des signes de comparaison < et >.
2.
a) Dans les exercices 2.a), 2.b) et 2.c), la règle implicite utilisée par cet élève est la décomposition d'un nombre décimal en milliers, centaines, dizaines…
2 kg 60 g = 2 × 1000 + 0 × 100 + 6 × 10 + 0 × 1 = 2060 g.
2 kg 60 g = 2 × 1000 + 0 × 100 + 6 × 10 + 0 × 1 = 2060 g.
b) Pour vérifier si l'élève utilise la règle qui donne en général un résultat faux « le 1e chiffre correspond au nombre de kilogrammes, le reste des chiffres correspond au nombre de grammes », on peut lui demander de compléter l'égalité suivante : 340 g = … kg … g et voir si l'élève commet l'erreur de répondre 3 k 40 g.
3.
a) Pour faire prendre conscience à l'élève de son erreur lors de l'égalité : 2 kg 40 g = 240 g, on peut proposer en parallèle les balances suivantes :
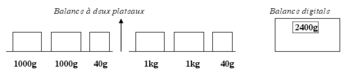 |
b) Pour aider l'élève qui écrit que 2 kg 40 g est égal à 240 g, l'enseignant peut le faire réfléchir sur les ordres de grandeur. Il peut expliquer que 240 g est très inférieur à 1000 g, que 1000 g est égal à 1 kg donc il n'est pas possible que 2 kg 40 g soit égal à 240 g.
