Dernier essai le
- Score :
/20
Sujet
Sujet
L'épreuve est notée sur 20. Une note globale égale ou inférieure à 5 est éliminatoire. Durée de l'épreuve : 3 h ; coefficient 1
Le sujet est composé de 5 exercices indépendants permettant de vérifier les connaissances du candidat.
Corrigé
Corrigé
Exercice 1
Affirmation 1 : FAUX
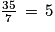
5 est un entier naturel. Or l'ensemble des entiers naturels est inclus dans l'ensemble des nombres décimaux, donc 5 est un nombre décimal. Donc
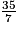 est un décimal.
est un décimal.Affirmation 2 : VRAI
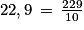
Donc 22,9 est bien un nombre rationnel.
On pouvait aussi affirmer que tout nombre décimal est un nombre rationnel (le contraire étant faux ; exemple :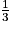 ).
).
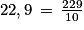
Donc 22,9 est bien un nombre rationnel.
On pouvait aussi affirmer que tout nombre décimal est un nombre rationnel (le contraire étant faux ; exemple :
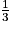 ).
).Affirmation 3 : VRAI
Soit n un nombre entier.
L'entier consécutif à n est l'entier n + 1.
Les suivants sont n + 2, n + 3, n + 4, n + 5 et n + 6.
La somme de ces sept entiers est égale à
S = n + (n + 1) + (n + 2) + (n + 3) + (n + 4) + (n + 5) + (n + 6)
S = 7n + 21
S = 7 × n + 7 × 3
On factorise la somme car on repère le facteur commun 7.
S = 7 × (n + 3)
Ainsi, la somme est bien un multiple de 7 car la somme S est égale au produit de 7 et d'un entier positif (n + 3).
Soit n un nombre entier.
L'entier consécutif à n est l'entier n + 1.
Les suivants sont n + 2, n + 3, n + 4, n + 5 et n + 6.
La somme de ces sept entiers est égale à
S = n + (n + 1) + (n + 2) + (n + 3) + (n + 4) + (n + 5) + (n + 6)
S = 7n + 21
S = 7 × n + 7 × 3
On factorise la somme car on repère le facteur commun 7.
S = 7 × (n + 3)
Ainsi, la somme est bien un multiple de 7 car la somme S est égale au produit de 7 et d'un entier positif (n + 3).
Affirmation 4 : VRAI
Déterminons les diviseurs de 496.
Par la calculatrice, en effectuant des divisions successives, on a :
496 = 2 × 2 × 2 × 2 × 31
Donc les diviseurs de 496 sont :
1, 2, 2 × 2, 2 × 2 × 2, 2 × 2 × 2 × 2, 31, 2 × 31, 2 × 2 × 31 et 2 × 2 × 2 × 31.
C'est-à-dire :
1, 2, 4, 8, 16, 31, 62, 124 et 248.
Calculons la somme de ces diviseurs :
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496.
496 est donc un nombre parfait.
Ce résultat est apparemment connu depuis l'Antiquité.
Déterminons les diviseurs de 496.
Par la calculatrice, en effectuant des divisions successives, on a :
496 = 2 × 2 × 2 × 2 × 31
Donc les diviseurs de 496 sont :
1, 2, 2 × 2, 2 × 2 × 2, 2 × 2 × 2 × 2, 31, 2 × 31, 2 × 2 × 31 et 2 × 2 × 2 × 31.
C'est-à-dire :
1, 2, 4, 8, 16, 31, 62, 124 et 248.
Calculons la somme de ces diviseurs :
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496.
496 est donc un nombre parfait.
Ce résultat est apparemment connu depuis l'Antiquité.
Affirmation 5 : FAUX
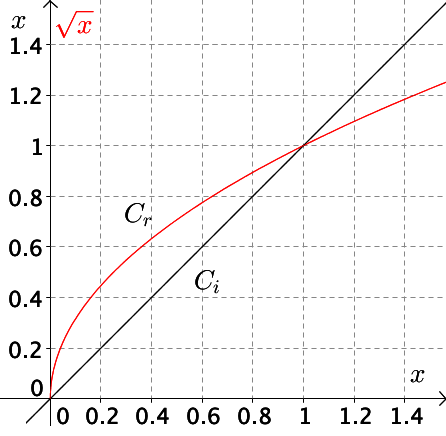
Les réels de l'intervalle ]0 ;1[ sont des réels ne vérifiant pas cette affirmation.
En effet, la fonction racine carrée est supérieure à la fonction identité sur [0 ;1].
Les réels de l'intervalle ]0 ;1[ sont des réels ne vérifiant pas cette affirmation.
En effet, la fonction racine carrée est supérieure à la fonction identité sur [0 ;1].
 |
Par exemple : pour 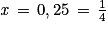
On a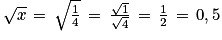 .
.
On a 0,25 < 0,5.
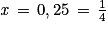
On a
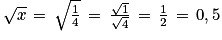 .
.On a 0,25 < 0,5.
Affirmation 6 : FAUX
Cela est faux en général. C'est vrai pour les carrés.
Si l'on plie une feuille A4 le long de l'une de ses diagonales, les deux parties ne se superposent pas.
Si l'on plie une feuille A4 le long de l'une de ses diagonales, les deux parties ne se superposent pas.
Exercice 2
1.
Considérons une grandeur (ici le volume en L) mesurée à deux reprises : au départ et à l'arrivée.
On note ces valeurs Vd et Va.
Alors le pourcentage d'évolution entre Vd et Va est le nombre égal à :
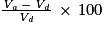
On calcule ainsi :
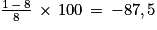
Ainsi, le volume a diminué de 87,5 %.
(On sait qu'il s'agit d'une diminution car −87,5 < 0 car Vd > Va.)
On note ces valeurs Vd et Va.
Alors le pourcentage d'évolution entre Vd et Va est le nombre égal à :
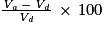
On calcule ainsi :
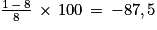
Ainsi, le volume a diminué de 87,5 %.
(On sait qu'il s'agit d'une diminution car −87,5 < 0 car Vd > Va.)
2.
On peut construire le tableau de proportionnalité suivant :
Ainsi, on a :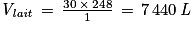 . Claire va donc récolter en moyenne 7 440 L de lait au total chaque jour.
. Claire va donc récolter en moyenne 7 440 L de lait au total chaque jour.
On a ensuite le tableau de proportionnalité suivant :
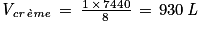
Claire pourra ainsi fabriquer 930 L de crème fraîche par jour (si elle a le temps de récolter le lait le matin et fabriquer la crème l'après-midi).
Enfin, on peut construire le tableau de proportionnalité suivant :
On a donc :
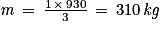
Ainsi, Claire peut espérer fabriquer 310 kg de beurre chaque jour.
| Nombre de vaches | 1 | 248 |
| Volume de lait (en L) | 30 | Vlait |
Ainsi, on a :
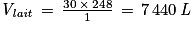 . Claire va donc récolter en moyenne 7 440 L de lait au total chaque jour.
. Claire va donc récolter en moyenne 7 440 L de lait au total chaque jour.On a ensuite le tableau de proportionnalité suivant :
| Volume de lait | 8 | 7 440 |
| Volume de crème fraîche | 1 | Vcrème |
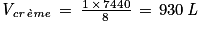
Claire pourra ainsi fabriquer 930 L de crème fraîche par jour (si elle a le temps de récolter le lait le matin et fabriquer la crème l'après-midi).
Enfin, on peut construire le tableau de proportionnalité suivant :
| Masse de beurre (en kg) | 1 | m |
| Volume de crème fraîche (en L) | 3 | 930 |
On a donc :
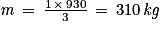
Ainsi, Claire peut espérer fabriquer 310 kg de beurre chaque jour.
3.
a. Le volume V d'un parallélépipède rectangle (pavé droit) est égal au produit l × L × h avec l la longueur, L la largeur et h la hauteur.
On vérifie que les grandeurs sont bien toutes exprimées dans la même unité.
V = 10 × 6,5 × 3,5 = 227,5 cm3
Ainsi, le volume d'une plaquette de beurre est égal à 227,5 cm3.
On vérifie que les grandeurs sont bien toutes exprimées dans la même unité.
V = 10 × 6,5 × 3,5 = 227,5 cm3
Ainsi, le volume d'une plaquette de beurre est égal à 227,5 cm3.
b. Pour comparer les deux masses volumiques, elles doivent être exprimées dans la même unité.
250 g est égal à 0,25 kg. En effet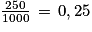 . On peut aussi le constater dans un tableau de conversion :
. On peut aussi le constater dans un tableau de conversion :
On utilise maintenant le tableau de conversion suivant :
On sait que 1 dm3 = 1 L.
On a 227,5 cm3 = 0,2275 dm3 = 0,2275 L
La masse volumique du beurre est donc égale à :
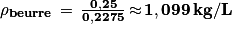
On a ainsi : ρbeurre > ρlait.
250 g est égal à 0,25 kg. En effet
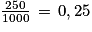 . On peut aussi le constater dans un tableau de conversion :
. On peut aussi le constater dans un tableau de conversion :| kg | hg | dag | g | dg | cg | mg |
| | 2 | 5 | 0 | | | |
On utilise maintenant le tableau de conversion suivant :
| dm3 (= litres) | cm3 | mm3 | ||||||
| | | 0 | 2 | 2 | 7 | 5 | | |
On sait que 1 dm3 = 1 L.
On a 227,5 cm3 = 0,2275 dm3 = 0,2275 L
La masse volumique du beurre est donc égale à :
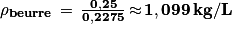
On a ainsi : ρbeurre > ρlait.
4.
a.
Le rectangle de la base du pavé droit a pour dimensions 10 cm par 6,5 cm.
Un patron possible est le suivant :
Un patron possible est le suivant :
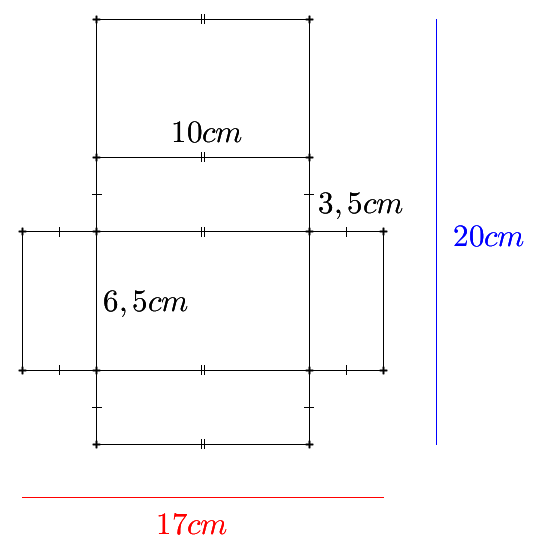 |
On a une longueur du patron égale à 3,5 + 10 = 3,5 = 17 cm.
On a une largeur du patron égale à 3,5 + 6,5 + 3,5 + 6,5 = 20 cm.
Ce patron requiert une feuille de dimension minimale de 17 cm × 20 cm. La feuille proposée a une dimension de 23 cm × 20 cm, cela est donc possible (car 23 > 17).
On a une largeur du patron égale à 3,5 + 6,5 + 3,5 + 6,5 = 20 cm.
Ce patron requiert une feuille de dimension minimale de 17 cm × 20 cm. La feuille proposée a une dimension de 23 cm × 20 cm, cela est donc possible (car 23 > 17).
b. Les dimensions de la plaquette sont l = 10 cm par L = 6,5 cm par h = 3,5 cm.
D'après notre patron, l'aire de la surface latérale de la plaquette est égale à la somme des aires de six rectangles.
Deux rectangles ont pour dimensions : 10 par 6,5.
L'aire de l'un de ces rectangles est égale à 10 × 6,5 = 65 cm2.
Deux rectangles ont pour dimensions : 10 par 3,5.
L'aire de l'un de ces rectangles est égale à 10 × 3,5 = 35 cm2.
Deux rectangles ont pour dimensions : 3,5 par 6,5.
L'aire de l'un de ces rectangles est égale à 3,5 × 6,5 = 22,75 cm2.
Ainsi, A = 2 × 65 + 2 × 35 + 2 × 22,75 = 245,5 cm2.
D'après notre patron, l'aire de la surface latérale de la plaquette est égale à la somme des aires de six rectangles.
Deux rectangles ont pour dimensions : 10 par 6,5.
L'aire de l'un de ces rectangles est égale à 10 × 6,5 = 65 cm2.
Deux rectangles ont pour dimensions : 10 par 3,5.
L'aire de l'un de ces rectangles est égale à 10 × 3,5 = 35 cm2.
Deux rectangles ont pour dimensions : 3,5 par 6,5.
L'aire de l'un de ces rectangles est égale à 3,5 × 6,5 = 22,75 cm2.
Ainsi, A = 2 × 65 + 2 × 35 + 2 × 22,75 = 245,5 cm2.
c. Calculons le rapport :
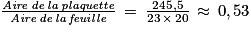
Claire a tort, l'aire de la plaquette représente environ 53 % de l'aire de la feuille (53 < 60).
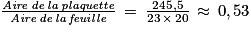
Claire a tort, l'aire de la plaquette représente environ 53 % de l'aire de la feuille (53 < 60).
5.
a. La formule qui peut être saisie en B9 est « =SOMME(B3 :B8) » (si le logiciel est paramétré en français) ou « =B3 + B4 + B5 + B6 + B7 + B8 ».
b. La formule qui peut être saisie en C3 est « =B3*2,5 ».
Attention : selon le logiciel, la version, la langue sélectionnée, le séparateur décimal peut être le point ou la virgule.
Attention : selon le logiciel, la version, la langue sélectionnée, le séparateur décimal peut être le point ou la virgule.
Exercice 3
Modélisons l'expérience aléatoire par un arbre de probabilité.
Notons T1 l'événement « JB touche la planche lors du 1er saut ».
Notons D1 l'événement « JB dépasse la planche lors du 1er saut ».
Notons R1 l'événement « JB réussit le 1er saut ».
Notons T2 l'événement « JB touche la planche lors du 2d saut ».
Notons D2 l'événement « JB dépasse la planche lors du 2d saut ».
Notons R2 l'événement « JB réussit le 2d saut ».
Notons T1 l'événement « JB touche la planche lors du 1er saut ».
Notons D1 l'événement « JB dépasse la planche lors du 1er saut ».
Notons R1 l'événement « JB réussit le 1er saut ».
Notons T2 l'événement « JB touche la planche lors du 2d saut ».
Notons D2 l'événement « JB dépasse la planche lors du 2d saut ».
Notons R2 l'événement « JB réussit le 2d saut ».
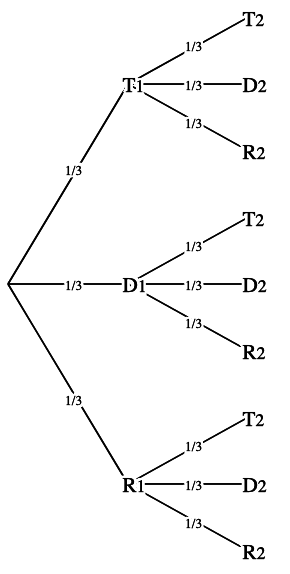 |
1.
On cherche donc la probabilité de l'événement « JB réussit le 1er saut et réussit le 2d saut ». Cet événement se note 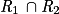 .
.
À retenir : l'union de deux événements se traduit par le symbole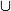 (comme dans le mot union) alors que l'intersection de deux événements se traduit par le symbole
(comme dans le mot union) alors que l'intersection de deux événements se traduit par le symbole  .
.
Un seul chemin de l'arbre correspond, on calcule donc :
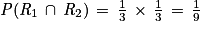
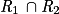 .
.À retenir : l'union de deux événements se traduit par le symbole
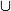 (comme dans le mot union) alors que l'intersection de deux événements se traduit par le symbole
(comme dans le mot union) alors que l'intersection de deux événements se traduit par le symbole  .
.Un seul chemin de l'arbre correspond, on calcule donc :
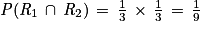
2.
L'événement donné se note 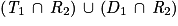 .
.
Visuellement on peut dire que l'événement proposé est composé de deux chemins :
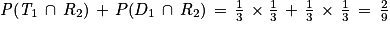
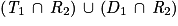 .
.Visuellement on peut dire que l'événement proposé est composé de deux chemins :
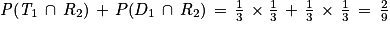
3.
Notons l'événement donné E. Alors 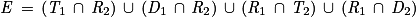 .
.
Les quatre événements sont disjoints deux à deux. On a donc :
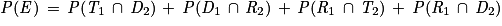
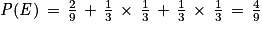
On pouvait aussi raisonner en termes de chemins et affirmer que les neuf chemins de l'arbre sont équiprobables et que les intersections des événements situés sur chaque chemin ont la même probabilité. Comme quatre chemins composent notre événement E, alors on a bien une probabilité de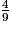 .
.
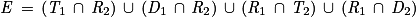 .
.Les quatre événements sont disjoints deux à deux. On a donc :
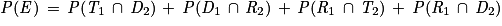
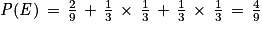
On pouvait aussi raisonner en termes de chemins et affirmer que les neuf chemins de l'arbre sont équiprobables et que les intersections des événements situés sur chaque chemin ont la même probabilité. Comme quatre chemins composent notre événement E, alors on a bien une probabilité de
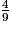 .
.4.
Notons F : « JB va mordre au moins une fois ».
Alors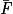 le contraire de F est « JB ne va pas mordre au moins une fois », c'est-à-dire « JB ne va mordre aucune fois. » Donc
le contraire de F est « JB ne va pas mordre au moins une fois », c'est-à-dire « JB ne va mordre aucune fois. » Donc 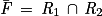 .
.
Rappel de propriété : Pour tout événement A, on a :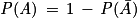 .
.
Ainsi :
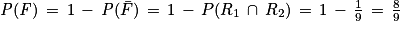
Ainsi, la probabilité qu'il morde au moins une fois lors de l'un de ses deux sauts est égale à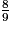 .
.
Alors
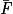 le contraire de F est « JB ne va pas mordre au moins une fois », c'est-à-dire « JB ne va mordre aucune fois. » Donc
le contraire de F est « JB ne va pas mordre au moins une fois », c'est-à-dire « JB ne va mordre aucune fois. » Donc 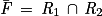 .
.Rappel de propriété : Pour tout événement A, on a :
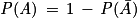 .
.Ainsi :
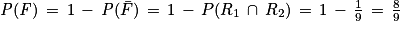
Ainsi, la probabilité qu'il morde au moins une fois lors de l'un de ses deux sauts est égale à
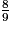 .
.Un document ressource Éduscol sur les probabilités peut être téléchargé ici.
Exercice 4
1.
Nous sommes en présence d'une configuration de Thalès (« en papillon »).
Des rappels sont disponibles si nécessaire sur le site blogpeda.ac-bordeaux.fr.
En effet, les points A, P, B et I, P, J sont alignés dans cet ordre.
Les droites (AI) et (JB) sont parallèles.
Ainsi, d'après le théorème de Thalès on peut affirmer que :
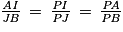
En particulier :
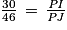
Ainsi :
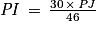
Or I, P et J sont alignés dans cet ordre, donc : IJ = IP + PJ ou encore PJ = IJ − IP.
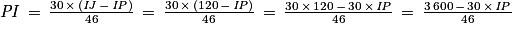
On cherche donc à résoudre l'équation suivante (en posant PI = x comme le propose l'énoncé) :
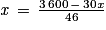
On multiplie les deux membres par 46.
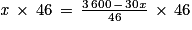
46x = 3 600 − 30x
On ajoute 30x aux deux membres.
46x + 30x = 3 600 − 30x + 30x
76x = 3 600
On divise les deux membres par 76.
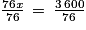
Ainsi :
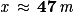
Les droites (AI) et (JB) sont parallèles.
Ainsi, d'après le théorème de Thalès on peut affirmer que :
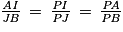
En particulier :
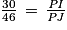
Ainsi :
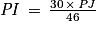
Or I, P et J sont alignés dans cet ordre, donc : IJ = IP + PJ ou encore PJ = IJ − IP.
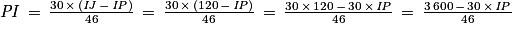
On cherche donc à résoudre l'équation suivante (en posant PI = x comme le propose l'énoncé) :
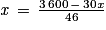
On multiplie les deux membres par 46.
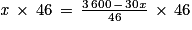
46x = 3 600 − 30x
On ajoute 30x aux deux membres.
46x + 30x = 3 600 − 30x + 30x
76x = 3 600
On divise les deux membres par 76.
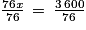
Ainsi :
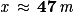
Des ressources pour réviser les résolutions d'équations sont disponibles sur le site Euler des mathématiques de l'académie de Versailles.
2.
a. Nous allons utiliser le théorème de Pythagore dans les triangles rectangles AIP et BPJ.
On a donc les égalités suivantes :
AP2 = AI2 + IP2 = 302 + x2
et
PB2 = JP2 + JB2 = (IJ − IP)2 + 462 = (120 − x)2 + 2 116
On a donc les égalités suivantes :
AP2 = AI2 + IP2 = 302 + x2
et
PB2 = JP2 + JB2 = (IJ − IP)2 + 462 = (120 − x)2 + 2 116
b. On va résoudre l'équation : PA = PB.
Or, si deux longueurs sont égales, alors leurs carrés sont égaux.
Ainsi : PA2 = PB2.
Donc :
302 + x2 = (120 − x)2 + 2 116
Rappel : (a −b)2 = a2 −2 × a × b + b2 (c'est la deuxième identité remarquable).
Ainsi, on résout :
302 + x2 = 1202 − 2 × 120 × x + x2 + 2 116
900 + x2 = 14 400 − 240x + x2 + 2 116
On soustrait par x2 les deux membres :
900 + x2 −x2 = 14 400 −240x + x2 + 2 116 −x2
900 = 14 400 −240x + 2 116
900 = 16 516 −240x
On ajoute 240x aux deux membres :
900 + 240x = 16 516 − 240x + 240x
900 + 240x = 16 516
On soustrait par 900 les deux membres :
900 + 240x − 900 = 16 516 − 900
240x = 15 616
Enfin, on divise les deux membres par 240 :
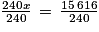
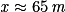
Or, si deux longueurs sont égales, alors leurs carrés sont égaux.
Ainsi : PA2 = PB2.
Donc :
302 + x2 = (120 − x)2 + 2 116
Rappel : (a −b)2 = a2 −2 × a × b + b2 (c'est la deuxième identité remarquable).
Ainsi, on résout :
302 + x2 = 1202 − 2 × 120 × x + x2 + 2 116
900 + x2 = 14 400 − 240x + x2 + 2 116
On soustrait par x2 les deux membres :
900 + x2 −x2 = 14 400 −240x + x2 + 2 116 −x2
900 = 14 400 −240x + 2 116
900 = 16 516 −240x
On ajoute 240x aux deux membres :
900 + 240x = 16 516 − 240x + 240x
900 + 240x = 16 516
On soustrait par 900 les deux membres :
900 + 240x − 900 = 16 516 − 900
240x = 15 616
Enfin, on divise les deux membres par 240 :
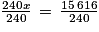
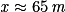
3.
a.
Calculons d la distance parcourue en mètres.
On sait que :
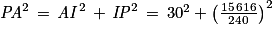
Donc :
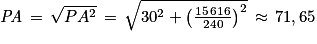
Et on sait que dans la situation choisie : PA = PB.
Ainsi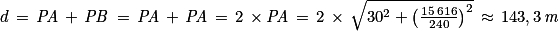 .
.
Comme la vitesse donnée est en km/h, alors convertissons cette distance en kilomètres en divisant notre résultat par 1 000.
La distance parcourue est donc d'environ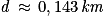 .
.
On a la formule suivante :
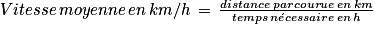
Donc :
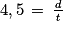
Soit :
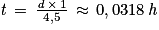
Or une heure est constituée de 60 minutes, d'où :
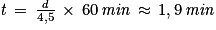
On peut convertir le résultat en secondes en multipliant à nouveau par 60 :
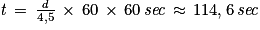
Soit un temps de parcours d'environ 1 minute et 55 secondes en arrondissant à la seconde.
On sait que :
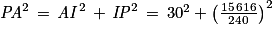
Donc :
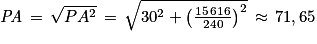
Et on sait que dans la situation choisie : PA = PB.
Ainsi
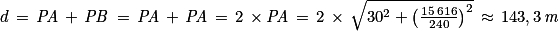 .
.Comme la vitesse donnée est en km/h, alors convertissons cette distance en kilomètres en divisant notre résultat par 1 000.
La distance parcourue est donc d'environ
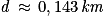 .
.On a la formule suivante :
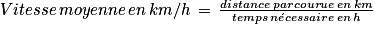
Donc :
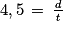
Soit :
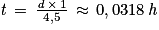
Or une heure est constituée de 60 minutes, d'où :
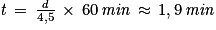
On peut convertir le résultat en secondes en multipliant à nouveau par 60 :
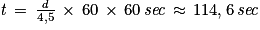
Soit un temps de parcours d'environ 1 minute et 55 secondes en arrondissant à la seconde.
b. On a la formule suivante :
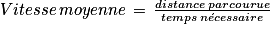
On a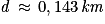 .
.
Déterminons le temps de parcours t en heures.
On a le tableau de proportionnalité suivant :
Donc :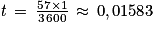 .
.
Ainsi :
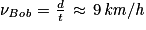
Ainsi, la vitesse de Bob est d'environ 9 km/h.
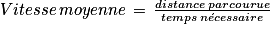
On a
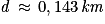 .
.Déterminons le temps de parcours t en heures.
On a le tableau de proportionnalité suivant :
| Heures | 1 | t |
| Secondes | 3 600 | 57 |
Donc :
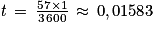 .
.Ainsi :
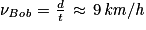
Ainsi, la vitesse de Bob est d'environ 9 km/h.
Exercice 5
1.
En utilisant la proportionnalité on trouve que :
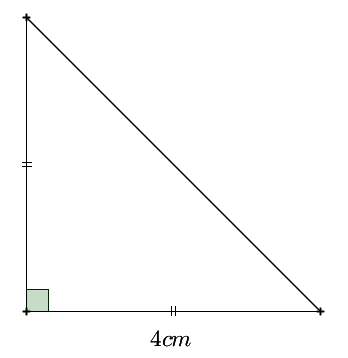 |
40 pas sont donc représentés par 4 cm sur la feuille.
2.
Le lutin va être orienté vers le bas.
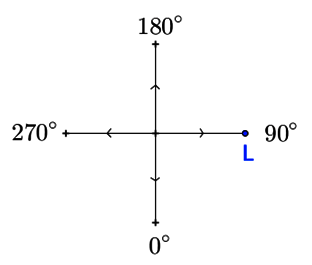
Initialement le lutin regarde vers la droite : le logiciel Scratch considère qu'il est orienté à 90°.
Initialement le lutin regarde vers la droite : le logiciel Scratch considère qu'il est orienté à 90°.
 |
Puis le lutin subit une rotation de 135° vers la gauche (dans le sens anti-horaire).
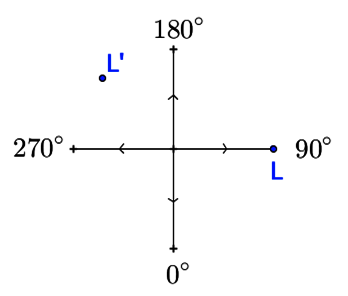 |
Son orientation est donc de 90° + 135° soit 225°.
Enfin le lutin subit une dernière rotation de 135° vers la gauche.
Enfin le lutin subit une dernière rotation de 135° vers la gauche.
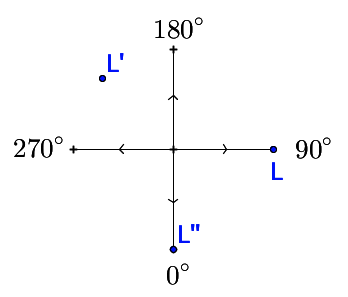 |
Son orientation finale est alors de 225° + 135° soit 360°.
L'orientation est donc « vers le bas » ou « vers le sud ».
L'orientation est donc « vers le bas » ou « vers le sud ».
3.
Pour tous les programmes, une boucle fermée « Répéter 4 fois » a été ajoutée.
Le programme A donne la figure 3.
En effet, à la fin du premier passage de la boucle qui dessine le triangle rectangle isocèle, le lutin (qui regarde vers le bas et est en position x = 0 et y = 0) va pivoter de 90° vers la gauche, il sera donc orienté vers la droite. Puis il va avancer de a + 10 pas avant de dessiner à nouveau le même triangle rectangle isocèle.
Le programme B donne la figure 1.
En effet, à la fin du premier passage de la boucle qui dessine le triangle rectangle isocèle, le lutin (qui regarde vers le bas et est en position x = 0 et y = 0) va redessiner un triangle rectangle isocèle mais en partant cette fois « vers le bas ».
Le programme C donne la figure 4.
En effet, à la fin du premier passage de la boucle qui dessine le triangle rectangle isocèle, le lutin (qui regarde vers le bas et est en position x = 0 et y = 0) va pivoter de 90° vers la gauche, il sera donc orienté vers la droite et en position x = 0 et y = 0.
La valeur de a est alors augmentée de 10 pas.
Lors du deuxième passage dans la boucle, le lutin va donc dessiner un triangle rectangle isocèle mais dont les deux côtés de même longueur auront pour longueur a + 10. Ce nouveau triangle vient d'une certaine manière « étendre » les côtés du triangle précédent. De même pour le troisième passage : le lutin dessinera un triangle rectangle isocèle dont les côtés ont pour longueur a + 10 + 10 soit a + 20.
Enfin, pour le quatrième et dernier passage, le lutin dessinera un triangle rectangle isocèle dont les côtés ont pour longueur a + 10 + 10 + 10 soit a + 30.
Le programme A donne la figure 3.
En effet, à la fin du premier passage de la boucle qui dessine le triangle rectangle isocèle, le lutin (qui regarde vers le bas et est en position x = 0 et y = 0) va pivoter de 90° vers la gauche, il sera donc orienté vers la droite. Puis il va avancer de a + 10 pas avant de dessiner à nouveau le même triangle rectangle isocèle.
Le programme B donne la figure 1.
En effet, à la fin du premier passage de la boucle qui dessine le triangle rectangle isocèle, le lutin (qui regarde vers le bas et est en position x = 0 et y = 0) va redessiner un triangle rectangle isocèle mais en partant cette fois « vers le bas ».
Le programme C donne la figure 4.
En effet, à la fin du premier passage de la boucle qui dessine le triangle rectangle isocèle, le lutin (qui regarde vers le bas et est en position x = 0 et y = 0) va pivoter de 90° vers la gauche, il sera donc orienté vers la droite et en position x = 0 et y = 0.
La valeur de a est alors augmentée de 10 pas.
Lors du deuxième passage dans la boucle, le lutin va donc dessiner un triangle rectangle isocèle mais dont les deux côtés de même longueur auront pour longueur a + 10. Ce nouveau triangle vient d'une certaine manière « étendre » les côtés du triangle précédent. De même pour le troisième passage : le lutin dessinera un triangle rectangle isocèle dont les côtés ont pour longueur a + 10 + 10 soit a + 20.
Enfin, pour le quatrième et dernier passage, le lutin dessinera un triangle rectangle isocèle dont les côtés ont pour longueur a + 10 + 10 + 10 soit a + 30.
Des ressources Éduscol sur la programmation en langage Scratch sont disponibles, à télécharger ici (les pages 13 et 14 concernent le dessin de figures).
Sujet corrigé réalisé par Jean Delautre, professeur de mathématiques au lycée Notre-Dame de la Paix à Lille.
Document précédent
Sujet 2025 de mathématiques, groupement académique 1 (nouveau)
Document suivant
Sujet 2025 de mathématiques, groupement académique 3 (nouveau)
